智能優化算法對提高分數階算子的有理逼近精度研究

徐 馳，趙慧敏，李 文

(1.大連交通大學 電氣信息學院，遼寧 大連 116028;2.大連交通大學 軟件學院，遼寧 大連 116028)*

0 引言

目前，分數階控制理論的研究內容已經十分豐富，其中主要包括分數階微積分算子的數值實現［1］、分數階控制器設計［2］、分數階系統辨識和分數階控制系統的系統性能分析及其分析方法［3］.在分數階控制的諸多研究方向中，分數階系統或算子模型的逼近方法研究是基礎.由于分數階微積分算子是復變量S的無理函數，要想對分數階系統進行數值仿真和實際應用就必須對分數階系統進行有理化近似.目前，在諸多分數階算子有理化近似方法中，人們多采用Oustaloup間接離散化方法［4］.該方法可以簡單并且直觀的根據參數計算公式來確定逼近傳遞函數，但是在所選定頻率范圍的低頻與高頻端的擬合效果不理想.實際上，當采用Oustaloup方法對分數階算子進行有理逼近時，一旦確定了有理函數的結構即逼近階次，那么根據參數計算公式可以發現逼近系數是對應于所選逼近頻段與逼近階次唯一確定的.因此要想在Oustaloup算法逼近頻段與逼近階次確定的基礎上提高其有理逼近精度，可以從有理傳遞函數的系數著手，通過合理的改變有理傳遞函數的系數來提高其有理逼近精度.為此，本文在Oustaloup算法基礎上采用粒子群優化算法對逼近傳遞函數的各系數進行尋優.在下面內容中，將對本文所提方法進行詳細闡述，并通過具體實例進行有效對比，證明所提方法的有效性.

1 Oustaloup算法

Oustloup算法也叫信號濾波法，在實際情況下，大多數分數階微分信號是無法預先知道的，那么我們可以通過構造濾波函數來實現對信號的數值處理.下面采用文獻［4］給出的Oustaloup算法對分數階微分算子進行有理逼近，得到有理傳遞函數:

這里選取擬合頻段為［0.01，100］、逼近階次為5.從式(1)可以看出分數階微分算子Sα(α=0.5)的有理逼近函數H(s)的一般形式為:

從Oustaloup算法的定義式也很容易證明式(2).

2 粒子群優化(PSO)算法

Kennedy和Eberhart基于對鳥群運行模式的簡化研究及行為模擬開發了一種優化算法—粒子群 優 化 算 法［5］(Particle Swarm Optimization，PSO).文獻［5］給出了粒子群優化算法的設計原理以及Matlab的相關程序實現.該算法的基本流程可歸納為:

Step1:在可行解空間內初始化所有微粒，包括在允許范圍內的隨機速度與位置.

Step2:評價每個微粒的位置適應值，計算其目標函數.

Step3:對于每個微粒，將其適應值與微粒自身所經歷過的最好位置(pbest)進行比較，若更好，則將其替換為當前的pbest.

Step4:對于每個微粒，將其適應值與整個群體所經歷過的最好位置(gbest)進行比較，若更好，則將其作為整個群體最優位置.

Step5:更新微粒的速度與位置.

Step6:若滿足終止條件，則停止迭代，否則返回Step2.

3 PSO算法對提高分數階算子有理逼近精度的研究

粒子群優化參數的選取包括粒子群初值、粒子群規模、慣性權重以及目標函數的確定:

(1)PSO初值的選取

因為所選逼近傳遞函數H(S)的階次為5，則位置矢量選取 Xi=(b1，b2，b3，b4，b5)，若要對分數階微分算子S0.5進行有理逼近精度提高的研究，那么位置矢量的初始值 Xi0=(10，298.5，1 218，768.5，74.79)，這樣可以有效的避免 PSO 尋優的隨機性，提高尋優效率.

(2)PSO慣性權重的選取

本文為了更好的平衡算法的全局搜索與局部搜索能力，采用線性遞減慣性權重［6］

ωstart為初始慣性權重、ωend是迭代至最大次數時的慣性權重、k為當前尋優次數、Tmax為最大迭代次數.根據經驗取 ωstart=0.9、ωsend=0.4、Tmax=300、微粒群規模m取30.

(3)目標函數的確定

分數階微分算子 Sα(α ∈［0.1 ～ 0.9］的實際頻域響應H(s)與其有理逼近函數的頻域響應之間的誤差包括幅值誤差(dB)和相位誤差(deg).因此，本文將粒子群優化算法的目標函數定義為幅值誤差絕對值和相位誤差絕對值之和:

H(ωi)為分數階算子的頻率響應，H^(ωi)為有理逼近函數的頻率響應，ωb＜ωi＜ωh.L為采樣個數，令 L=logspace(ωb，ωh，500).當尋優過程中，逼近函數H^(ωi)穩定時，目標函數取幅值誤差絕對值和相位誤差絕對值之和.當H^(ωi)不穩定時，目標函數值賦予一個較大值F.

4 仿真實例

用上述介紹的粒子群優化算法對分數階微分算子Sα(α=0.5)的有理逼近函數H(S)的各系數進行尋優，尋優結果為:

此時目標函數值f=0.789.

由式(5)可得S0.5的有理逼近函數(s)

繪制出(1)和(6)的Bode圖，如圖1所示(圖中疊加了S0.5的理論值):

圖1 Oustaloup算法和PSO算法比較

從圖1可以得出本文所提的PSO算法逼近精度高于Oustaloup算法，尤其在選取特定頻段的端點處擬合效果明顯優于Oustaloup算法.

下面分別采用Oustaloup算法和PSO算法對一個分數階傳遞函數進行有理逼近，并對兩種仿真進行對比.設要逼近的傳遞函數為:

將式(7)改寫為:

采用本文所提方法對分數階微分算子S0.2、S0.7進行有理傳遞函數系數尋優，得到:

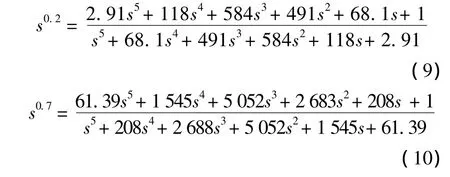
圖2給出了傳遞函數G(S)理論Bode圖和Oustaloup算法、本文所提方法得到的有理逼近函數的Bode圖，從圖中可以看出本文所提方法得到的有理傳遞函數擬合精度優于Oustaloup算法.

圖2 整個系統的Bode比較

從圖2可以發現，在中頻段兩種方法均能取得較好的逼近精度，而在低頻段與高頻段采用PSO算法的逼近精度明顯高于Oustaloup算法.

下面用Oustaloup算法對分數階微分算子Sα(α=(0.1 ～ 0.9)，得到有理逼近傳遞函數H(s)，再運用本文所提方法對分數階微分算子Sα(α=(0.1 ～ 0.9)的有理逼近函數H(S)的各系數進行尋優，最后分別計算出采用Oustaloup方法和本文方法的幅值絕對誤差平均值和相位絕對誤差平均值，對比結果如表1所示.

表1 Oustaloup算法與PSO算法誤差對比

從表1可以看出，對于 α ∈［0.1 ～ 0.9］，PSO算法的相位誤差均值明顯小于Oustaloup算法.當階次α＞0.3時，PSO算法的幅值誤差均值也比Oustaloup算法的幅值誤差均值小.當階次α∈［0.1～0.3］時，PSO算法的幅值誤差均值比Oustaloup方法的幅值誤差均值要大一點，不過在α＜0.3時，這兩種方法的幅值誤差均值都已足夠小，因此不影響PSO算法的優越性.

5 結論

本文提出的一種智能優化算法對提高分數階算子逼近精度的研究，該方法能夠有效的提高擬合精度，此方法所采用的有理傳遞函數結構由Oustaloup算法得到，有理逼近傳遞函數的分子、分母通過粒子群優化算法再次尋優得到.通過本文所提方法對分數階微分算子S0.5進行有理逼近，仿真結果表明所提方法能夠取得比Oustaloup算法更高的逼近效果.此外，還利用本文所提方法對一個分數階傳遞函數進行有理逼近，結果同樣證明了所提方法的有效性.

［1］高朝邦，周激流.基于四元數分數階方向微分的圖像增強［J］.自動化學報，2011，37(2):150-159.

［2］HARTLEY T T，LORENZO C F.Dynamics and control of initialized fractional order systems［J］.Nonlinear Dynamics，2002，29(1/2/3/4):201-233.

［3］MALTI R，VIETOR S，OUSTALOUP A，et al.An optimal instrumental variable method for continuous-time fractional model identification［C］.Proceeding of the 17thWorld Congress on The international Federation of Auto-mation Control Korea，2008:14379-14348.

［4］OUSTALOUP A，LEVRON F，NANOT F，et al.Frequency-band complex noninteger differentiator:characterization and synthesis［J］.IEEE Transactions on Circuits Systems I:Fundamental Theory and Applications，2000，47(1):25-39.

［5］BIRGE B，PSOT.A Particle Swarm Optimization Toolbox for matlab［J］.IEEE Swarm Intelligence Symposium Proceedings，2003，26(3):24-26.