城市軌道交通系統(tǒng)的適用性評價

左忠義，李 鑫

(大連交通大學 交通運輸工程學院，遼寧 大連 116028)*

0 引言

隨著我國城市化發(fā)展的加速，人們對于出行需求大幅增加，加之私家車數(shù)量的極速增加，城市的交通擁堵問題十分嚴重.結合城市自身特點建設適合的公共交通，優(yōu)先發(fā)展公共交通是解決城市擁堵問題的最佳途徑.城市軌道交通系統(tǒng)是一種運量大、快速、安全、環(huán)保節(jié)能的城市公共交通系統(tǒng)，同時對改善出行條件，引導城市局部發(fā)展方面做出很大貢獻，因此已經廣泛應用于國內外的許多城市.但是由于各個城市的自然條件、經濟條件以及已經建成的公共交通水平都各不相同，那么到底什么樣的城市適合軌道交通的發(fā)展是現(xiàn)在所面臨的問題.因此本文對城市軌道交通的適用性問題進行研究，從而能夠客觀合理的進行城市軌道交通的建設.

目前對于適用性的評價方法常用的有層次分析法、模糊綜合評價法等，應用這些方法進行評價時并不能克服實驗過程的隨機性和主觀性.因此本文采用BP神經網(wǎng)絡的評價方法，可以有效的避免上述評價方法的不足，客觀公正的對軌道交通的適用性進行評價，保證軌道交通合理、適度的建設.

1 城市軌道交通適用性分析

交通系統(tǒng)的適用性［1-4］具體體現(xiàn)在服務方面、成本方面、環(huán)境影響方面和社會環(huán)境影響方面.城市軌道交通的適用性就是指城市軌道交通技術設備，運營條件等滿足城市居民使用的能力，讓城市軌道交通與城市之間相互適應，達到整體條件下的最優(yōu).城市軌道交通的適用性要求城市軌道交通的建設與城市整體規(guī)劃的要求相適應，與環(huán)境的發(fā)展和維護相適應，并且建設施工過程中的安全因素也制約著城市軌道交通的適用性.

2 基于BP神經網(wǎng)絡城市軌道交通適用性評價模型的構建

2.1 BP 神經網(wǎng)絡

BP神經網(wǎng)絡的全稱是反向傳播學習算法模型(Back-Propagation Network)，它是人工神經網(wǎng)絡當中應用最廣泛的網(wǎng)絡模型之一，同時也體現(xiàn)了人工神經網(wǎng)絡當中最最核心的部分.BP神經網(wǎng)絡完整的理論是由 Rumelhart· Hinton 與 Williams［5］提出的，它是由輸入層、輸出層和隱含層構成的多層前向網(wǎng)絡，其具體的結構圖如圖1所示.

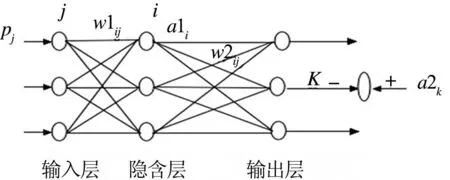
圖1 BP神經網(wǎng)絡簡化結構圖

根據(jù)圖可以看出，各層與各層之間采用的是全互連方式，而同層單元之間則無相互連接.輸入的信號從輸入節(jié)點輸入傳遞到隱含層節(jié)點，然后傳向輸出層，每一層的節(jié)點輸出只影響下一層節(jié)點的輸出.

BP神經網(wǎng)絡在進行科學實驗的時候，對于網(wǎng)絡層數(shù)的選取，神經元個數(shù)的確定，傳遞函數(shù)的確定以及選擇什么樣的訓練算法，都沒有具體的選擇參考標準，因此只能通過大量的實驗來確定.由于計算量很大，所以采取計算機和相關的軟件代替人工進行實驗計算.神經網(wǎng)絡工具箱(Neural Network Toolbox)簡稱NNT，該工具箱中包含了很多神經網(wǎng)絡常用的模型，還涵蓋很多常用的學習算法，并且計算機軟件的計算速度遠遠高于手工計算，因此本文在進行城市軌道交通適用性評價時就是采用的MATLAB軟件中的神經網(wǎng)絡工具箱進行實驗.

2.2 BP神經網(wǎng)絡評價模型中評價指標體系的確定

根據(jù)城市軌道交通系統(tǒng)的特點進行分析總結，結合城市軌道交通適用性的相關概念，在評價指標建立規(guī)則的指導下，建立了影響城市軌道交通的適用性的評價指標體系［6］，對大連市能否建設軌道交通進行驗證評價.由于沈陽、哈爾濱和長春與大連規(guī)模相當，并且都屬于東北三省，相互之間存在著一定的競爭關系，所以也將它們三個城市加入到樣本的驗證.相關的指標數(shù)值如表1所示.

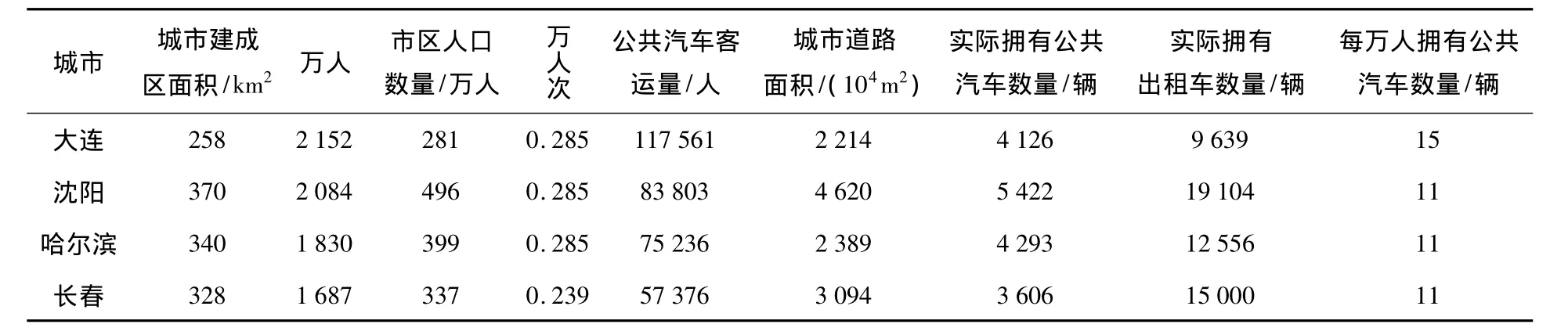
表1 相關城市的評價指標數(shù)值

2.3 BP神經網(wǎng)絡的構建

本文運用MATLAB軟件中的newff函數(shù)進行BP神經網(wǎng)絡的構建.那么在MATLAB中newff的調用命令如下:

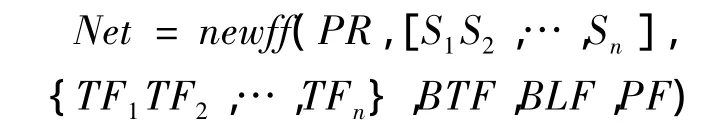
Net為BP網(wǎng)絡的生成對象;PR表示維的輸入矢量中介于每維的輸入的最大值與最小值之間的范圍;［S1S2，…，Sn］表示BP網(wǎng)絡的N層神經層中每層的神經元的數(shù)量;{TF1TF2，…，TFn}表示BP網(wǎng)絡的N層神經層中每層的傳遞函數(shù);BTF表示BP神經網(wǎng)絡使用的訓練函數(shù);BLF表示權值和閥值的學習算法，PF表示性能函數(shù).

針對本研究要解決的實際問題，對BP神經網(wǎng)絡評價模型的具體構建如下:

(1)神經網(wǎng)絡的層數(shù)的確定

已經有相關的理論證明:只有一層隱含層的神經網(wǎng)絡系統(tǒng)能夠應用任意精度來表示任意的連續(xù)函數(shù)，也就是說使用三層的神經網(wǎng)絡就可以完成任意精度的任意n維到m維的映射.因此本論文的神經網(wǎng)絡確定的層數(shù)為三層.

(2)傳遞函數(shù)的確定

BP神經網(wǎng)絡中提供了三種傳遞函數(shù)，分別是非線性logsig傳遞函數(shù)、非線性tansig傳遞函數(shù)和線性purelin傳遞函數(shù).經過以前學者的研究得出，一個具有兩層的神經網(wǎng)絡，如果第一層選取logsig函數(shù)，而第二層選取例如purelin的線性函數(shù)就可以模擬任何連續(xù)有界的函數(shù).因此確定logsig函數(shù)為隱含層的傳遞函數(shù)，確定purelin函數(shù)為輸出層的傳遞函數(shù).

(3)訓練函數(shù)的確定

根據(jù)表2可以看出traingd訓練函數(shù)、traingda訓練函數(shù)、traingdm訓練函數(shù)、traingdx訓練函數(shù)都需要進行了5000次的訓練，并且得到的收斂精度也是比較低的.而trainlm訓練函數(shù)只用了29次訓練就達到了的收斂精度，所以選擇trainlm函數(shù)作為訓練函數(shù).

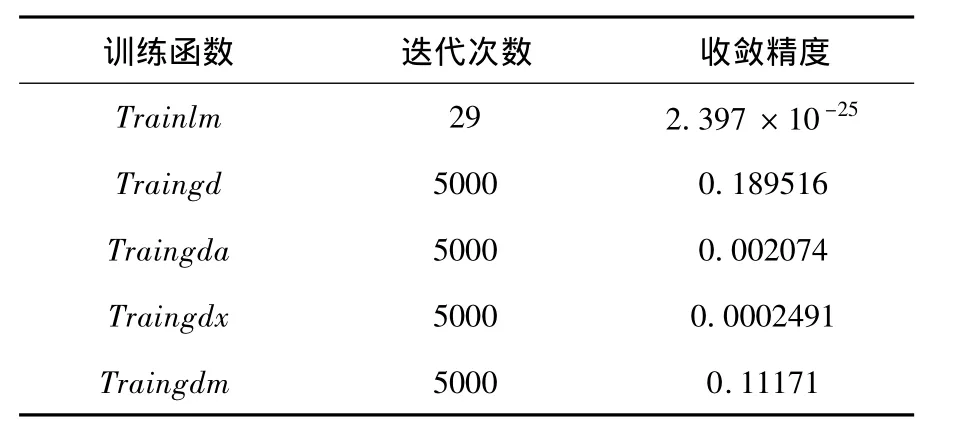
表2 不同訓練函數(shù)的訓練結果

(4)訓練參數(shù)的確定

確定訓練函數(shù)為trainlm，根據(jù)上面的實驗可以得出trainlm的訓練次數(shù)較少，所以確定BP神經網(wǎng)絡的最大學習次數(shù)為1 000，網(wǎng)絡的最大允許誤差為0.000 01，這些參數(shù)的設定在MATLAB中采用的函數(shù)是net.trainParam函數(shù)來進行的，那么具體的調用命令如下:

(5)各層的神經元個數(shù)的確定

輸入層的神經元個數(shù)是通過建立的評價指標體系來確定的，本文以9作為輸入層的神經元個數(shù).而以1作為輸出層的神經元個數(shù).因此對于各層的神經元的個數(shù)的確定，主要是指隱含層的神經元的個數(shù)確定.根據(jù)本論文第三章中的第三小節(jié)中的公式，可以計算出隱含層的神經元個數(shù)的范圍是在5～13之間.

本研究采用實驗的方法來確定隱含層的神經元個數(shù)，其中設定訓練次數(shù)為1 000，目標精度為0.000 01，以神經元個數(shù)5為例，其它的數(shù)值只是對命令中的神經元個數(shù)進行替換，調用命令如下:

根據(jù)表3可以得出，訓練次數(shù)并不是隨著神經元個數(shù)的增加而減少，收斂精度與神經元的個數(shù)也不是成規(guī)則的反比關系.最終通過整體數(shù)據(jù)可以得出，當隱含層的神經元個數(shù)為10時，它的訓練次數(shù)最少為6次，收斂精度較高，故選擇10個隱含層神經元.

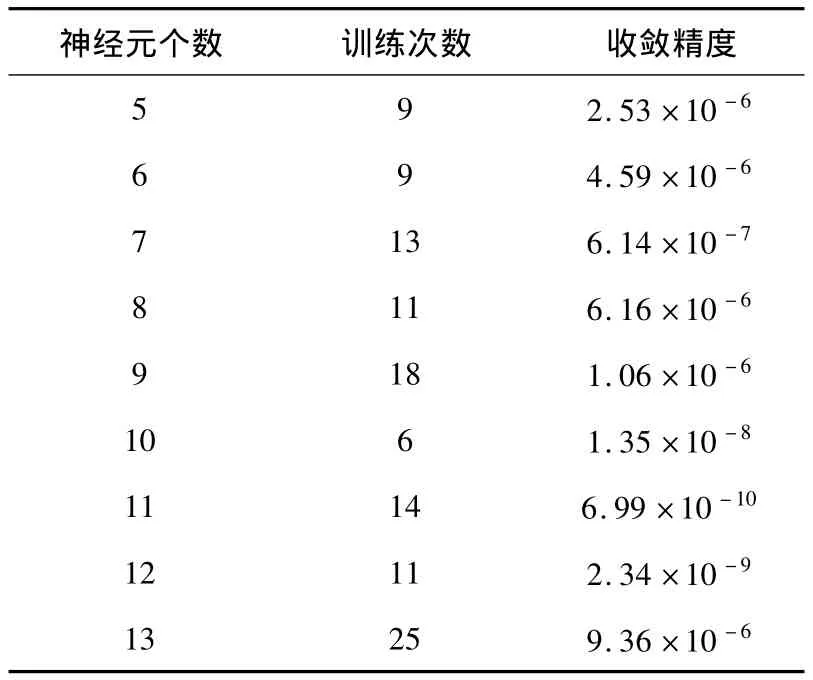
表3 神經元個數(shù)數(shù)值表

綜上所述，本研究構建的BP神經網(wǎng)絡為為三層神經網(wǎng)絡，它們分別是輸入層、隱含層和輸出層.輸入層神經元個數(shù)為9個，隱含層神經元個數(shù)為10個，輸出層神經元個數(shù)為1個.隱含層的傳遞函數(shù)為logsig函數(shù)，輸出層傳遞函數(shù)選擇為purelin函數(shù)，訓練函數(shù)定為trainlm函數(shù).最大學習次數(shù)為1000次，最大允許誤差定為0.00001.所以調用命令為:

建立的BP神經網(wǎng)絡的結構圖如圖2所示:

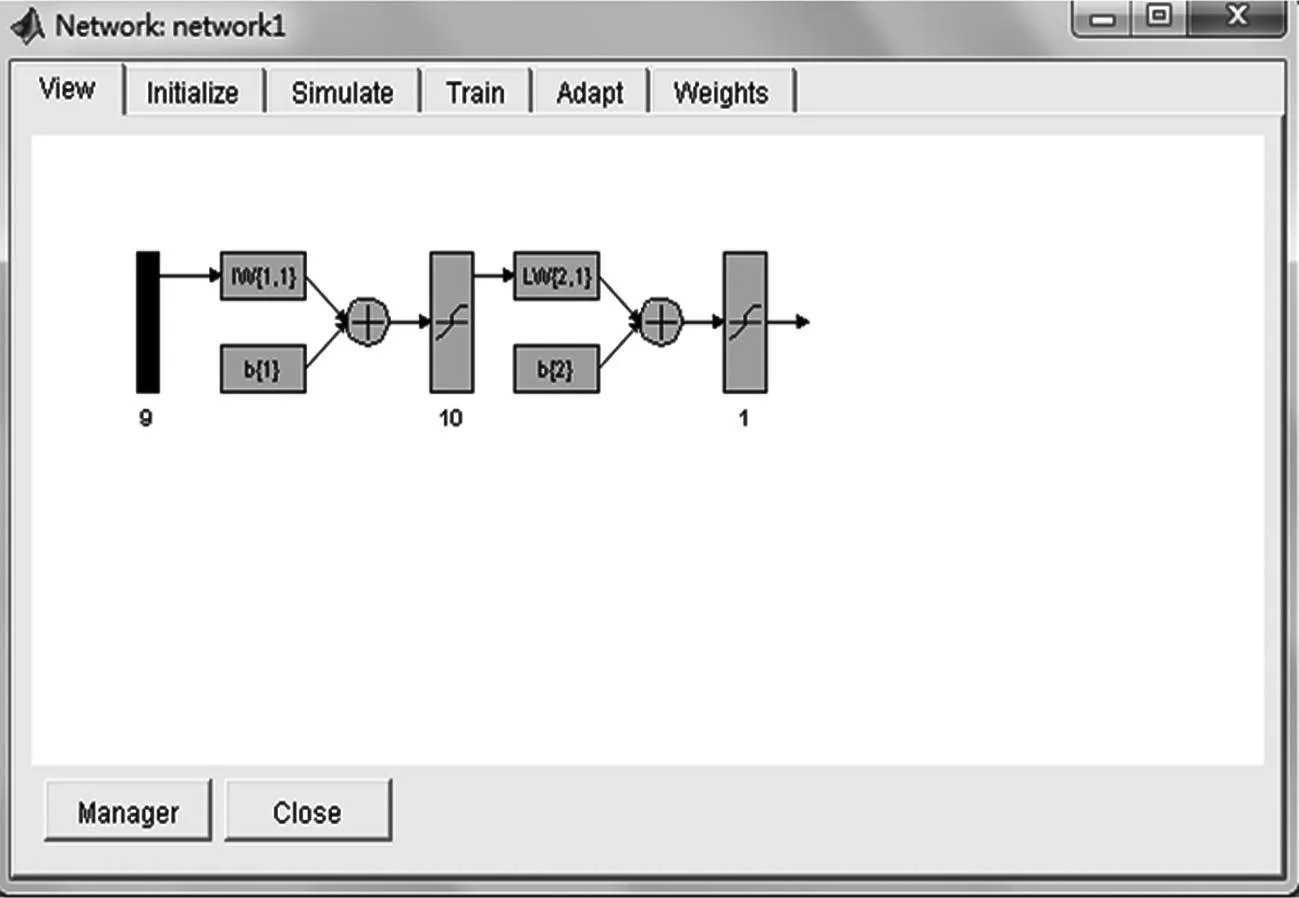
圖2 建立的BP神經網(wǎng)絡結構圖

2.4 BP神經網(wǎng)絡的仿真應用

對于BP神經網(wǎng)絡訓練后的網(wǎng)絡需要進行仿真，本文選用MATLAB中的sim函數(shù)進行仿真訓練.Sim函數(shù)的調用命令如下:

［Y，Pf，Af，E，perf］=sim(net，P，Pi，Ai，T)其中:Y表示網(wǎng)絡輸出;Pf表示訓練終止時的輸入延遲狀態(tài);Af表示訓練終止時的層延遲狀態(tài);E表示輸出和目標矢量之間的誤差;Perf表示網(wǎng)絡的性能;

Net表示要仿真的神經網(wǎng)絡;P表示網(wǎng)絡的輸入;Pi表示輸入延遲的初始狀態(tài);Ai表示層延遲的初始狀態(tài);T表示目標矢量.

由于在進行BP神經網(wǎng)絡實驗的時候，將輸入的數(shù)據(jù)都進行了歸一化處理，因而對于輸出的數(shù)據(jù)也是已經歸一化處理后的數(shù)據(jù)，為了更好的跟原始數(shù)據(jù)進行比較，需要將歸一化的輸出數(shù)據(jù)進行還原.運用MATLAB中的postmnmx調用命令進行數(shù)據(jù)還原，具體調用命令如下:

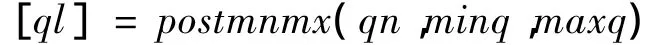
3 實例分析

運用建立的BP神經網(wǎng)絡在MATLAB中進行大連市的實例驗證時，同樣要進行樣本的歸一化處理，在此采用的歸一化處理函數(shù)為tramnmx函數(shù);驗證完成后，對于輸出的結果，需要進行反歸一化處理，采用的調用函數(shù)為postmnmx函數(shù).那么在MATLAB軟件中具體的驗證調用命令如下:

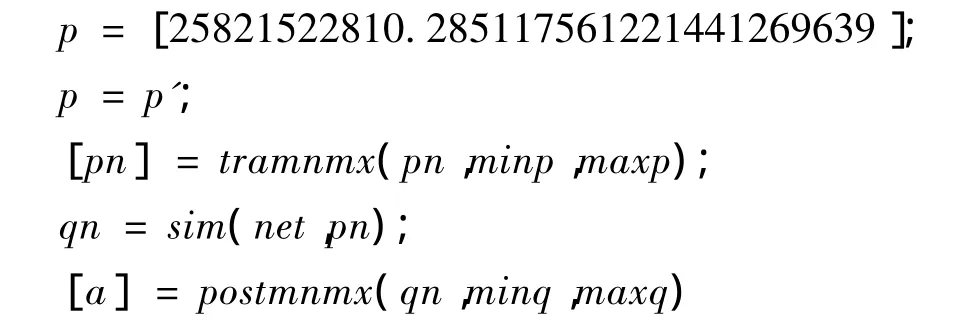
將上文建立的綜合評價指標輸入，建立的神經網(wǎng)絡的輸出數(shù)據(jù)如表4所示.

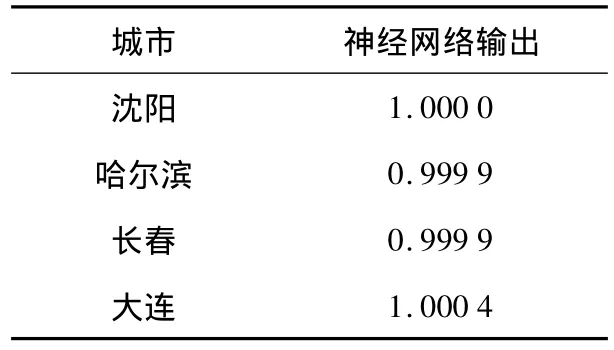
表4 神經網(wǎng)絡的輸出結果

如果城市的各項評價指標在MATLAB軟件中通過神經網(wǎng)絡運算出的結果接近1，則說明軌道交通適用于該城市;如果運算輸出的結果接近0，則說明軌道交通不適用于該城市.根據(jù)表4的輸出結果可以得出，四個城市的輸出結果都接近數(shù)字1.因此可以得出結論，城市軌道交通適用于沈陽、哈爾濱、長春和大連四個城市的城市建設.

4 結論

本文采用的BP網(wǎng)絡進行城市軌道交通適用性的評價分析是科學可行的，得出的結論也是可信的.通過BP神經網(wǎng)絡計算輸出的結果與實際情況相符，證明了該模型的準確性，可以進行實際應用.與此同時在大連市建設城市軌道交通能夠緩解城市的擁堵，減輕傳統(tǒng)公共交通的壓力，提高乘客的服務水平，推動城市的未來發(fā)展.并且大連市在經濟、技術、客流等方面都具備建設城市軌道交通的實力.

通過運用BP神經網(wǎng)絡進行城市軌道交通適用性的評價，可以科學的評判軌道交通是否適用于該城市.這樣就可以合理有效的推進城市軌道交通的建設與發(fā)展，從而避免超前或者滯后建設.對于不具備建設軌道交通的城市，可以通過其他的方式緩解城市的交通問題，如建設公交專用道、提高公共交通服務水平等方法.

［1］張琦.新型軌道交通系統(tǒng)在上海的適用性分析［J］.交通與運輸:學術版，2013(2):101-104.

［2］秦武.空中軌道交通系統(tǒng)的適用性分析［J］.城市公用事業(yè)，2012(6):17-21.

［3］張生，魏濤，彭燕.長沙 BRT系統(tǒng)適用性研究［J］.湖南交通科技，2004(1):109-112.

［4］徐偉.海口市快速公交系統(tǒng)適用性分析［J］.福建建設科技，2013(2):80-82.

［5］Barnard.Optimization for training neural nets［J］.IEEE Trans.On Neural Networks，1992，3(2):232-240.

［6］中國城市統(tǒng)計年鑒2006年［M］.北京:中國統(tǒng)計出版社，2006.