基于雜波脊先驗信息的非均勻雜波抑制方法

同亞龍， 王　彤， 代保全， 吳建新

(西安電子科技大學雷達信號處理國家重點實驗室， 陜西 西安 710071)

?

基于雜波脊先驗信息的非均勻雜波抑制方法

同亞龍， 王彤， 代保全， 吳建新

(西安電子科技大學雷達信號處理國家重點實驗室， 陜西 西安 710071)

摘要：機載雷達回波數據非均勻會在很大程度上削弱傳統空時自適應處理算法的雜波抑制性能。為此，提出一種基于雜波脊先驗信息的非均勻雜波抑制方法，利用機載雷達雜波信號在角度多普勒平面的譜分布信息構造導向矢量基，并在考慮陣元誤差影響情況下，對待檢測單元數據進行迭代的最小二乘擬合，最后對擬合后的剩余數據進行恒虛警檢測處理。該方法充分利用了雷達系統參數及雜波譜分布等先驗信息，并且不需要訓練樣本，可以較好地抑制非均勻雜波，從而改善機載雷達的檢測性能。仿真實驗驗證了該方法的有效性。

關鍵詞：機載雷達; 空時自適應處理; 非均勻雜波; 先驗信息; 雜波脊

0引言

機載雷達安裝在高空平臺上，其相對于地基雷達具有探測距離遠、覆蓋范圍廣等優越性。但同時由于載機平臺的運動及下視工作狀態，機載預警雷達也面臨著比地基雷達更為復雜的雜波環境。因此，要檢測雜波背景中的運動目標，雜波抑制則是其必須要解決的難題。經過40多年的發展，空時自適應處理(space-time adaptive processing，STAP)技術[1-3]被證明是現有最好的雜波抑制方法，它能夠同時從空間和時間上區分雜波和目標，可以在很大程度上改善機載預警雷達的雜波抑制及運動目標檢測性能，特別對低速目標和被旁瓣雜波所遮蔽的弱小目標的檢測更為有利。

由于雜波背景的統計特性未知，傳統的STAP處理器通常假設回波數據服從獨立同分布條件(independent and identically distributed，IID)，通過選取待檢測單元(cell under test，CUT)周圍的距離樣本估計出CUT內的雜波協方差矩陣，以形成自適應濾波權系數，對雷達系統所接收到的空時兩維回波數據進行最優線性組合，從而最大化輸出信雜噪比。然而，由于實際場景中存在多變的地形高程、地表類型、植被覆蓋等情況，以及旁瓣目標、孤立干擾等的影響，機載預警雷達通常都工作在非均勻環境中[4]，使得STAP處理器很難獲得足夠的IID樣本，導致STAP技術的雜波抑制性能嚴重下降。

對此類由于數據非均勻性導致的STAP性能下降問題，常用的解決辦法是在自適應濾波之前級聯非均勻檢測器(non-homogeneity detector，NHD)，對數據樣本是否滿足IID條件做出判斷，從而剔除有損自適應算法性能的非均勻樣本數據[5-9]。這類方法能在一定程度上提高非均勻環境下的檢測性能，但存在2個主要問題。首先，當環境非均勻性嚴重時，NHD需要剔除大量的奇異樣本，使得可用于進行自適應權值訓練的樣本數更少甚至不足，在小樣本情況下的STAP性能得不到有效提高；其次，此類算法關注的都是如何更好地去除訓練樣本中的非均勻性，而存在于CUT內的孤立非均勻雜波信號得不到有效抑制，導致大量虛警。為解決傳統基于統計的STAP算法無法抑制CUT內的孤立干擾問題，人們提出了一種非統計的直接數據域(direct data domain，DDD)方法[10-11]，通過最小化一維或兩維對消以后的CUT數據功率的方式，在保護目標信號的同時對旁瓣孤立干擾源進行有效抑制。但這種方法只適用于空時均勻采樣情況，對非矩形面陣系統或非均勻合成子陣系統等情況無效；由于未進行雜波統計特性的估計，無法對CUT內的均勻雜波分量進行有效抑制；基于對消的目標保護方式，一方面犧牲了空時孔徑，性能損失通常大于3 dB[12]，另一方面當存在陣元誤差等非理想因素時，無法對目標信號進行有效保護，容易造成目標相消。

本文提出一種基于雜波脊先驗信息的非均勻雜波抑制方法，該方法利用機載雷達所接收到的地雜波在角度多普勒平面上的譜分布特征(通常稱作雜波脊)，如正側面陣系統的雜波分布為直線，非正側面陣為橢圓形狀[2]，構造出一組雜波導向矢量基，在考慮陣元誤差影響情況下，對CUT內的雜波分量在最小二乘約束下進行迭代擬合，然后對擬合后的剩余數據進行恒虛警檢測，從而完成對非均勻雜波信號的充分抑制以及對運動目標的可靠檢測。仿真實驗結果驗證了本文方法的有效性。

1信號模型

考慮正側視機載雷達的運動目標檢測問題。假設雷達天線為一N元等距線陣，一個相干處理間隔內的脈沖數為M。將第n個陣元第m次快拍的接收數據記為xnm，則第n個陣元的數據矢量x(n)可表示為

(1)

式中，(·)T表示轉置操作。將x(n)(n=1,2,…,N)排列成NM×1的列矢量x，即

(2)

則雷達運動目標檢測問題可轉化為如式(3)的二元假設檢驗問題：

H0:x=xc+xn

(3)

式中，假設H0和H1分別表示CUT回波中不存在或者存在目標信號；xt，xc和xn分別表示目標、雜波以及噪聲分量。下面分別給出其具體的信號模型。

目標回波信號xt可表示為

(4)

式中，α表示目標信號的復幅度；st表示目標信號的空時導向矢量，其表達式為

(5)

式中，?表示Kronecker積操作；st,s和st,t分別表示目標信號的空域導向矢量和時域導向矢量，其具體形式為

(6)

式中，ft,s=dcos(θt)cos(φt)/λ表示目標信號的歸一化空間頻率；θt和φt分別為目標相對于雷達的方位角和俯仰角；d和λ分別為雷達陣元間距及工作波長；ft,d=2vt/(λfr)表示目標信號的歸一化多普勒頻率；vt表示目標相對于雷達的徑向速度；fr表示脈沖重復頻率。

雜波回波信號xc[2]可表示為

(7)

式中，Nr表示距離模糊數；Nc表示距離環中獨立散射體個數；αc,pq表示第p次模糊距離單元中第q個雜波塊的回波復幅度；sc,pq為其相應的空時導向矢量，其定義如式(5)和式(6)。

噪聲信號xn主要由接收機噪聲和環境噪聲組成，其中接收機噪聲可建模為高斯白噪聲，而環境噪聲較為復雜，具有一定的空域相關性[2]。

當陣列天線不存在誤差時，天線上的每個陣元具有一致的幅相特性，此時由式(4)～式(7)所給出的信號模型可以較好地表征機載雷達回波中的各種信號分量。但在實際陣列天線中，受機械加工等因素的影響，不可避免地存在著各種誤差，這也就意味著式(6)所采用的理想陣列流型已不再合適，此時需要考慮誤差對陣列天線的影響。本文主要考慮陣元誤差這一典型情況[13-15]，其誤差模型可以表示為

(8)

此時，可構造陣元誤差空時錐削矩陣T為

(9)

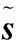
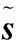
(10)

(11)

由式(10)可以看出，當存在陣元誤差時，真實的目標導向矢量由2部分組成，第1部分對應理想的信號模型，第2部分為陣元誤差對理想信號流型的調制。由此可見，受陣元誤差的影響，DDD算法中基于理想信號模型的對消方式并不能完全濾除目標信號，無法對目標信號進行有效保護，從而引起目標自相消現象，使得雷達的運動目標檢測性能嚴重下降。

2雜波秩分析

對于正側陣雷達系統，假設存在一地面雜波塊，相對于雷達的方位角和俯仰角分別為θc和φc，則其歸一化空間頻率和歸一化多普勒頻率分別為

(12)

(13)

式中，v為載機速度。則其空時頻率之間具有如下關系

(14)

式(14)表明正側陣雷達系統的地雜波回波信號的空時頻率滿足線性關系，即雜波脊在角度多普勒平面內為一條直線，式(14)中的β即為這條直線的斜率。

假設各雜波塊之間相互獨立，則雷達接收到的雜波信號所對應的空時協方差矩陣可以表示為

(15)

式中，σc,pq=E{|αc,pq|2}表示第p次模糊距離單元中第q個雜波塊的回波能量；E{·}表示求期望操作。根據Brennan準則[2]可知，雜波協方差矩陣Rc的秩為

(16)

當考慮陣元誤差影響時，雜波協方差矩陣可用式(9)給出的空時錐削矩陣T進行修正，即

(17)

Hadamard積有這樣的重要性質[16]：當矩陣A和B為同維矩陣時，有rank(A⊙B)≤rank(A)rank(B)。因此，由式(16)可以得出

rank(Rc)

(18)

式(18)說明，陣元誤差的存在不會增加雜波協方差矩陣的秩。

3基于雜波脊信息的雜波抑制方法

本文所提非均勻雜波抑制算法的動機與可行性是基于下面的事實：無論工作在什么樣的非均勻環境中，機載雷達接收到的地面雜波在角度多普勒平面的譜分布軌跡(即雜波脊)都具有一定的特點，如正側面陣機載雷達的雜波脊為直線，而斜側面陣雷達的雜波脊為橢圓。而且，雜波脊的形狀和位置只取決于天線陣面的幾何構型、平臺運動速度以及雷達系統參數，而與實際雜波的統計特性無關。一方面，對于實際的雷達系統來說，上述陣面構型或者系統參數等信息是已知的，利用這些先驗信息可以計算出CUT中的雜波信號在角度多普勒平面內的分布，即估計出雜波脊的位置；另一方面，地雜波的非均勻性一般都反映在統計特性上的差異，當不同訓練樣本中雜波的統計特性相差較大時，常規STAP算法的雜波抑制性能就會由于協方差矩陣估計不準確而嚴重下降，但我們注意到，無論雜波是均勻或者非均勻，它在角度多普勒平面內的分布都是固定的。

當然，根據已知的參數信息估計出來的雜波脊是理想情況下的雜波分布，當存在陣元誤差、互耦、雜波內部運動等非理想因素時，理論雜波脊會有一定程度的偏離或展寬。因此，在考慮典型非理想因素情況下，充分利用雜波脊先驗信息，設計出針對非均勻雜波信號的抑制算法是個可行途徑。

下面對本文所提算法進行詳細闡述。在所假設的正側陣系統中，當天線陣元以半波長等間距排布時，回波數據中地雜波信號將占據整個歸一化的空間頻率范圍。因此，首先對完整的歸一化頻率區間[0,1]進行rc點的均勻離散化，即得到離散的空間頻率點fc,s,r=(r-1)/rc(r=1,2,…,rc)。根據式(14)的線性關系即可確定相應的多普勒頻點，這樣就得到了rc組落在雜波脊曲線上的空時頻點

(19)

(20)

(21)

式中，al∈Crc×1為第l個距離門數據在所給基下的擬合系數。此處的最小二乘擬合問題為凸優化問題，可直接采用優化軟件工具CVX[17]求解。由于陣元誤差Es通常未知，本文采用迭代最小二乘的方式對陣元誤差和擬合系數進行聯合估計，從而實現對CUT數據中的雜波分量的充分抑制，并得到雜波抑制后的剩余數據yl:

(22)

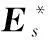
本文算法的詳細操作步驟總結如下。

步驟 1根據系統參數確定雜波脊位置，然后對雜波脊上的空時頻點進行離散化處理。

步驟 3參數初始化：陣元誤差Es=1N，數據范數zl=‖xl‖2，噪聲電平σl，迭代差值δl=σl。

步驟 4代入Es，求解式(21)的優化問題，得到擬合系數al。

步驟 5代入al，求解式(21)的優化問題，得到陣元誤差Es。

步驟 7判斷是否zl大于σl并且δl大于0.01σl：是，執行步驟4；否，執行步驟8。

步驟 8根據式(22)計算剩余數據yl。

步驟 9對各距離門數據對應的剩余數據進行CA-CFAR檢測，輸出目標檢測結果。

4仿真實驗

本節通過仿真數據實驗對所提算法的有效性進行驗證。為了能夠客觀、真實地反映出實際工作中機載預警雷達所接收到的回波數據的非均勻性，本文數據仿真中采用了歐空局和魯汶大學于2010年聯合發布的全球陸地覆蓋數據GlobCover2009[18]以及美國航天局與國防部國家測繪局于2000年獲得的全球數字高程數據SRTM[19]。仿真場景中心(即載機位置)的經緯度分別為-76.724 9°和38.999 2°，位于美國東海岸的Delmarva半島，該地區有明顯的陸海交界、城市及山區等地形地貌，雷達回波具有明顯的非均勻性，可以更好地檢查本文算法的有效性。另外，仿真中加入了10%的幅度誤差和6°的相位誤差。系統仿真參數如表1所示。

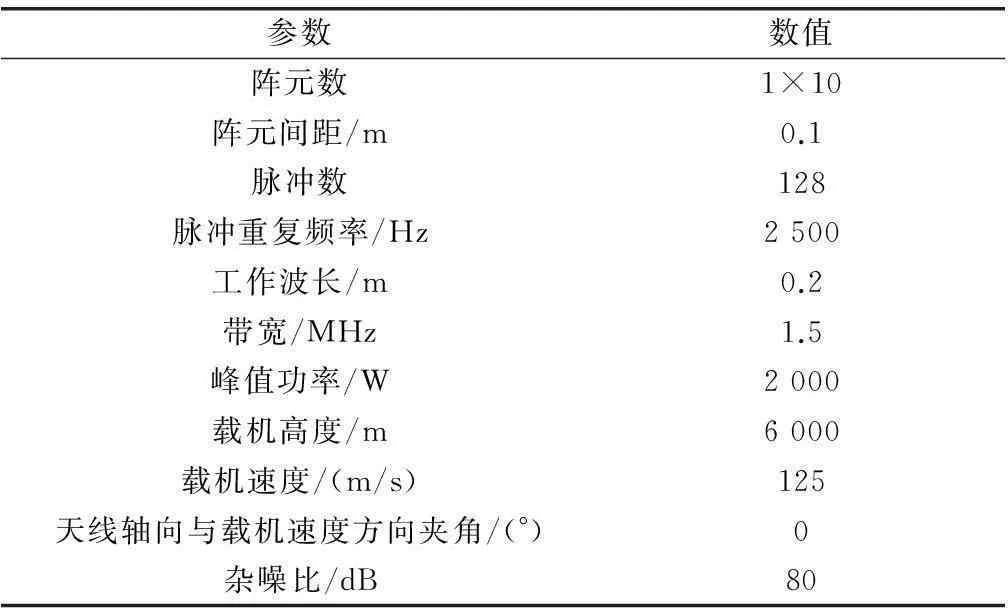
表1　仿真參數

圖1給出了仿真數據的脈沖多普勒處理結果。圖中深色區域為散射系數較低的水域回波，從圖中可以看到數據中存在著明顯的水陸交界，這與仿真場景地形地貌一致，也與美國空軍研究實驗室(AFRL)主導的MCARM項目所獲得的實測數據的處理結果[20]非常相似，說明了本文根據地形數據仿真得到的機載雷達回波數據具有一定的可信度，能夠真實反映雷達實際工作中遇到的非均勻環境。

圖1　仿真數據的脈沖多普勒處理結果

另外，為了更好地反映本文算法相對于已有算法的性能優勢，仿真數據中注入了5個強旁瓣孤立干擾點信號和4個運動目標信號，這些信號的空域陣列流型也存在著相同的陣元誤差，具體參數如表2所示。這些強的旁瓣孤立干擾點信號可以假設來自于具有比背景雜波強得多的雷達后向散射系數的地面物體，如橋梁、鐵塔和角反射器等，有助于增強仿真數據的非均勻性。

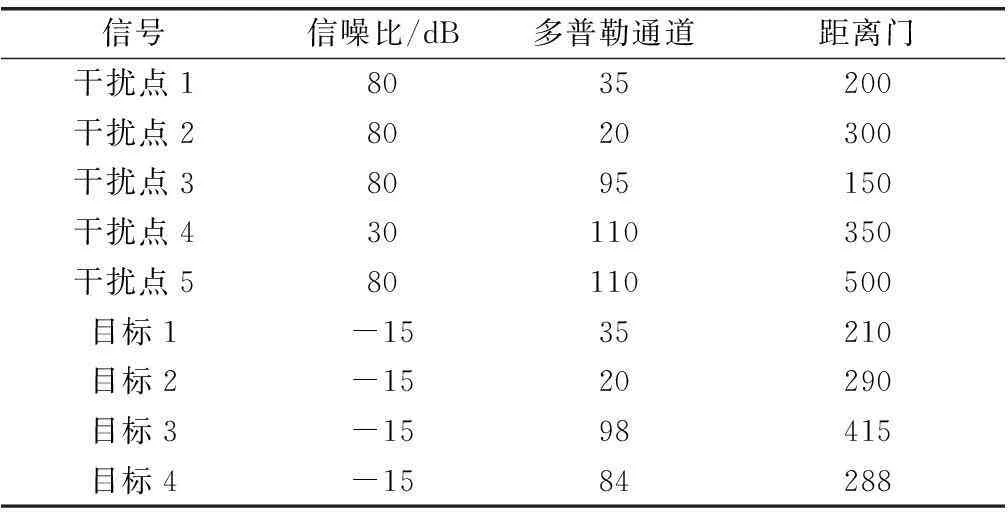
表2　注入信號參數

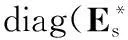
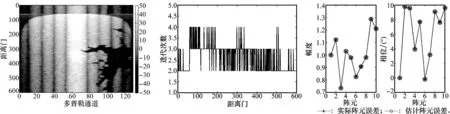
圖2　擬合數據的脈沖多普勒處理結果　　　　　　　　　　圖3　迭代次數　　　　　　　　　圖4　估計誤差與真實誤差比較

下面本文通過2組實驗結果對所提算法的有效性進行說明。在機載雷達數據處理中，當回波中包含大量孤立干擾及陸海交界等信號分量，具有很強的非均勻性時，通常采取的做法就是在自適應處理前級聯一種或多種NHD，如基于廣義內積(generalized inner product，GIP)的NHD，從全部或部分距離樣本中挑選出符合條件的均勻樣本，進行自適應權值的訓練，從而提高自適應算法在非均勻雜波環境中的處理性能。另外，由于實際機載雷達系統自由度通常都很大，全維自適應處理不可實現，因此數據處理中也都采取降維STAP的方法，擴展因子化方法(extended factored approach，EFA)[21]和聯合域局域化(joint domain localized，JDL)方法[22]就是其中比較典型的常用方法。因此，為了進一步考察所提算法的有效性，本文也給出了基于GIP樣本選擇的EFA和JDL算法的處理結果，文中分別簡記為GIP-EFA和GIP-JDL。除此之外，本文還給出了基于單距離樣本的直接數據域算法的處理結果，該算法通過空時二維滑窗獲取足夠的訓練樣本進行自適應權值的訓練，從而避免了臨近距離門訓練樣本的非均勻問題，文中記作DDD。圖5依次給出的是GIP-EFA、GIP-JDL、DDD和本文算法處理后CFAR檢測的輸出結果。從圖5(a)和圖5(b)中可以看出，傳統方法GIP-EFA和GIP-JDL無法對所加入的孤立干擾信號進行有效抑制，在檢測結果中出現大量虛警；這些強的孤立干擾的存在會抬高自適應處理后的CFAR檢測門限，造成對弱目標信號的漏警，目標信號1和2就因此而無法被檢測到；另外，目標信號3和4位于海陸交界處，由于無法獲得足夠的均勻樣本數據而不能對目標信號的背景雜波進行有效估計和抑制，使得這2個目標仍然湮沒在較強的剩余雜波中而無法得到檢測。從圖5(c)可以看出，DDD算法雖然規避了臨近距離門樣本非均勻問題，但空時子孔徑平滑過程會造成自由度損失，影響了自適應算法的雜波抑制效果，導致虛警增加；而且在存在陣元幅相誤差情況下，DDD算法的對消過程無法有效濾除樣本數據中的目標分量，引起目標自相消問題，造成漏警。從圖5(d)中本文算法的檢測結果可以看到，孤立干擾信號都得到了有效抑制，目標信號也都可以被檢測出來；相對于其他2種算法，本文算法檢測到的虛警也更少。

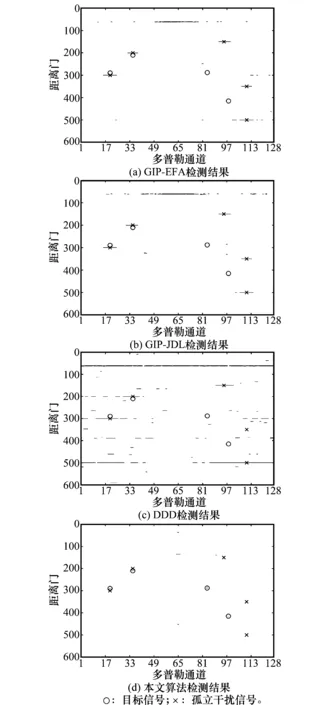
圖5　檢測結果比較

圖6給出了GIP-EFA、GIP-JDL、DDD和本文算法的檢測概率曲線。實驗中，選取第11～50號多普勒通道、第401～500號距離門范圍內的數據做總共4 000次的蒙特卡羅實驗，虛警概率設置為0.01。從圖中可以看出，GIP-EFA和GIP-JDL的檢測性能比較一致，而本文算法的檢測性能遠好于其他2種算法，如當檢測概率為0.8時，本文所提算法有超過3dB的性能優勢。而在陣元誤差及自由度損失影響下，DDD算法在給定的信噪比范圍內基本無法實現對目標信號的檢測。

圖6　檢測概率曲線

5結論

針對機載預警雷達中的非均勻雜波抑制問題，本文提出一種基于雜波脊先驗信息的雜波抑制方法。該方法在充分考慮陣元誤差影響情況下，利用構造的導向矢量基對雷達回波數據進行迭代的最小二乘估計，可以實現對非均勻雜波的充分擬合及抑制。基于數字地形數據的雷達回波仿真實驗驗證了本文算法的有效性。需要說明的是本文僅考慮了存在陣元誤差情況下的正側陣天線系統中的雜波抑制情況，對于非正側陣構型以及存在其他類型非理想因素的情況將在后續工作中進一步研究。

參考文獻：

[1] Brennan L E, Reed I S. Theory of adaptive radar[J].IEEETrans.onAerospaceandElectronicSystems,1973,9(1):237-252.

[2] Ward J. Space-time adaptive processing for airborne radar TR-1015[R]. Lexington:MIT Lincoln Laboratory, 1994.

[3] Klemm R.Principlesofspace-timeadaptiveprocessing[M]. London:the Institution of Electrical Engineers, 2002.

[4] Melvin W L. Space-time adaptive radar performance in heterogeneous clutter[J].IEEETrans.onAerospaceandElectronicSystems, 2000, 36(2):621-633.

[5] Wu H, Wang Y L, Chen J W. Nonhomogeneous detector for STAP based on spectral center frequency method[J].SystemsEngineeringandElectronics, 2008, 30(4):606-608.(吳洪, 王永良, 陳建文. 基于頻心法的STAP非均勻檢測器[J].系統工程與電子技術, 2008, 30(4):606-608.)

[6] Chen Y X, Gao L N. Nonhomogeneous detector for STAP based on local template technique[J].JournalofNationalUniversityofDefenseTechnology,2013,35(3):132-137.(陳宇翔,高立寧.基于局域模板的STAP非均勻檢測器[J].國防科技大學學報,2013,35(3):132-137.)

[7] Yang X P, Liu Y X, Long T. Robust non-homogeneity detection algorithm based on prolate spheroidal wave functions for space-time adaptive processing[J].IETRadar,SonarandNavigation,2013,7(1):47-54.

[8] Aghaabdellahian N, Modarres-Hashemi M. Improving performance of adaptive radar detectors in nonhomogeneous environment[C]∥Proc.ofthe21stIranianConferenceonElectricalEngineering, 2013:1-6.

[9] Chen S J, Kong L J, Yang J Y. Target detection for heterogeneous cyclostationary sea clutter[J].Circuits,Systems,andSignalProcessing, 2014, 33(3):959-971.

[10]AdveRS,HaleTB,WicksMC.Practicaljointdomainlocalisedadaptiveprocessinginhomogeneousandnonhomogeneousenvironments-part2:nonhomogeneousenvironments[J].IEE Proceedings of Radar, Sonar and Navigation, 2000, 147(2):66-74.

[11]AhmadiM,MohamedpourK,KeshvariF.Directdatadomain(D3)approach for space-time adaptive processing in colocated MIMO radar[C]∥Proc.of the 21st Iranian Conference on Electrical Engineering, 2013:1-4.

[12]YangZW,HeS,LiaoGS,etal.Directdatadomainapproachwithspace-timeadaptiveprocessingforarbitrarylineararray[J].Acta Electronica Sinica,2011,39(12):2900-2904.(楊志偉,賀順,廖桂生,等.任意線陣的直接數據域空時自適應處理方法[J].電子學報,2011,39(12):2900-2904.)

[13]LiJF,ZhangXF,GaoX.Ajointschemeforangleandarraygain-phaseerrorestimationinbistaticMIMOradar[J].IEEE Geoscience and Remote Sensing Letters,2013,10(6):1478-1482.

[14]CaoSH,YeZF,HuN,etal.DOAestimationbasedonfourth-ordercumulantsinthepresenceofsensorgain-phaseerrors[J].Signal Processing, 2013, 93:2581-2585.

[15]JiangL,WangT.Arrayerrorestimationusingsubspace-basedapproach[J].Systems Engineering and Electronics,2014,36(4):656-660.(姜磊,王彤.基于子空間的陣元誤差估計方法[J].系統工程與電子技術,2014,36(4):656-660.)

[16]HornRA,JohnsonCR. Topics in matrix analysis[M].England:CambridgeUniversityPress, 1991.

[17]GrantM,BoydS.CVX:matlabsoftwarefordisciplinedconvexprogramming[EB/OL].[2014-7-20].http:∥www.stanford.edu/～boyd/cvx.

[18] 中國科學院計算機網絡信息中心全球變化參量數據庫[EB/OL].[2014-7-20].http:∥globalchange.nsdc.cn.

[19] 中國科學院計算機網絡信息中心國際科學數據服務平臺[EB/OL].[2014-7-20].http:∥srtm.datamirror.csdb.cn.

[20]SloperD,FennerD,ArntzJ,etal.Multi-channelairborneradarmeasurement[R].NewYork:RomeLaboratory,1996.

[21]DipietroR.Extendedfactoredspace-timeprocessingforairborneradarsystem[C]∥Proc.of the 26th Asilomar Conference on Signals, Systems and Computing, 1992:425-430.

[22]WangH,CaiL.Onadaptivespatial-temporalprocessingforairbornesurveillanceradarsystems[J].IEEE Trans. on Aerospace and Electronic Systems, 1994, 30(3):660-669.

同亞龍(1987-)，男，博士研究生，主要研究方向為陣列信號處理、空時自適應信號處理。

E-mail：yalong.t@163.com

王彤(1974-)，男，教授，博士，主要研究方向為機載雷達運動目標檢測、合成孔徑雷達。

E-mail：twang@mail.xidian.edu.cn

代保全(1985-)，男，博士研究生，主要研究方向為陣列信號處理、空時自適應信號處理。

E-mail：dbqhao@163.com

吳建新(1982-)，男，副教授，博士，主要研究方向為陣列信號處理、空時自適應信號處理及動目標檢測。

E-mail：jxwu@xidian.edu.cn

網絡優先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20141128.0838.001.html

Heterogeneous clutter suppression method based on the

knowledge of clutter ridge

TONG Ya-long， WANG Tong， DAI Bao-quan， WU Jian-xin

(NationalLabofRadarSignalProcessing,XidianUniversity,Xi’an710071,China)

Abstract:The heterogeneity of echo data in airborne radar can severely degrades the clutter suppression performance of conventional space-time adaptive processing (STAP)algorithms. To address this issue, a heterogeneous clutter suppression method based on the prior knowledge of clutter ridges is presented. A set of steering vector basis is first constructed by utilizing the spectral characteristics of the ground clutter seen by airborne radar, and then used to fit the test data in an iterative least mean-square manner with the presence of the array error under consideration. Subsequently, the constant false alarm rate detection is conducted on the residual data. This method makes full use of the prior knowledge of radar system parameters and clutter spectral structure and does not need any training samples, which can effectively suppress the heterogeneous clutter and significantly improve the detection performance of the airborne radar. Simulation results validate the effectiveness of the proposed method.

Keywords:airborne radar; space-time adaptive processing(STAP); heterogeneous clutter; prior knowledge; clutter ridge

作者簡介：

中圖分類號：TN 959.73

文獻標志碼：ADOI:10.3969/j.issn.1001-506X.2015.05.09

基金項目：國家自然科學基金(61372133，61471285)；中央高校基本科研業務費專項資金(K50511020008)資助課題

收稿日期：2014-07-29；修回日期：2014-10-23；網絡優先出版日期：2014-11-28。