Toeplitz矩陣有限等距特性研究

陳忠輝, 熊　蕓

(福州大學物理與信息工程學院, 福建 福州 350116)

?

Toeplitz矩陣有限等距特性研究

陳忠輝, 熊蕓

(福州大學物理與信息工程學院, 福建 福州 350116)

摘要：在壓縮感知熱潮的影響下,觀測矩陣的有限等距特性(restricted isometry property, RIP)也受到廣泛關注。大多數理論研究表明高斯隨機矩陣是滿足RIP特性的,但由于其存儲成本較高,物理實現較復雜,在實際使用中托普利茲(Toeplitz)隨機矩陣由于可以使用快速離散傅里葉變換實現而受到青睞。該文將圖論中點均勻著色定理和蓋爾圓盤定理應用于壓縮感知中,對托普利茲觀測矩陣的RIP特性進行了證明,證明結果表明,由服從某種特定概率分布的項構造的Toeplitz矩陣以較大概率滿足有限等距特性。最后,對最小二乘算法(least square,LS)、線性最小均方誤差(linear minimum mean square error,LMMSE)算法和高斯觀測矩陣的壓縮感知算法以及Toeplitz觀測矩陣的壓縮感知算法進行了對比分析,Toeplitz觀測矩陣的壓縮感知算法在性能方面要優于高斯觀測矩陣的壓縮感知算法和傳統算法,運算復雜度方面要優于高斯隨機矩陣,為壓縮感知實現無失真地重構原始信號提供了理論和應用參考。

關鍵詞：觀測矩陣; 有限等距特性; 均勻著色; 蓋爾圓盤定理

0引言

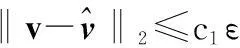
圖的染色理論是圖論中的一個重要分支,在現實生活中有很多問題,例如排序問題、工作分配問題、無線電頻率分配問題、衛星通訊問題等最終都可以歸結為圖的染色問題。染色按照點邊的不同又分為點染色,邊染色和全染色等[8]。該文創造性地將圖的均勻著色理論應用于觀測矩陣RIP的證明。

觀測矩陣RIP-3k性質的一個等價描述是ΘT的奇異值或由ΘT構成的Gram矩陣Gr(ΘT)=(ΘT)TΘT的特征值位于區間(1-δ3k,1+δ3k)。Ger?chgorin圓盤定理是矩陣特征值估計的一個基本定理,指出矩陣Mn×n的所有特征值包含在以對角線元素為圓心的n個圓盤的并集中。這種天然的聯系使得應用Ger?chgorin圓盤定理于RIP特性證明成為可能。

1圖論著色模型數學描述

圖的著色理論是圖論的重要組成部分,圖的著色主要有點著色和邊著色,點著色由可以細分為均勻著色,松弛著色和樹著色。圖G的一個正常k-頂點著色是指k種顏色在V上的一種分配,使得任意2個相鄰的頂點分配以不同顏色。若圖G有一個正常k-頂點著色,就稱G是k-頂點可著色的。

設φ是圖G的一個正常的頂點著色,φ的任何2種不同顏色所染的頂點數目至多相差1,稱φ是G的一個均勻著色。如果φ是圖G的一個均勻k-頂點著色,稱φ是G的一個均勻k-頂點著色。有限、簡單圖由G=G(V(G),E(G))來描述,簡寫為G=G(V,E)。V(G)為圖G的頂點集合,V(G)的元素為圖G的頂點,圖G的頂點個數稱為它的階;E(G)稱為圖G的邊集合,E(G)的元素為圖G的邊;在圖G中與頂點u相鄰的頂點的全體叫作u的鄰域,記作NG(u),稱NG(u)為頂點u的度數,記作dG(u)。同時稱度數為k的頂點為k-點。Δ(G)和δ(G)分別表示圖G的最大自由度和最小自由度。

實際上,圖論著色方法可用于很多觀測矩陣具有統計結構相關性的情況下,該文所闡述的是均勻著色在觀測矩陣的有限等距特性證明的應用,重點目標就是將由觀測矩陣構成的無向簡單圖G劃分為若干個完全非連通子圖,也就是獨立集。我們給出如下的例子進行說明：對于一個5階無向簡單圖,均勻點著色方案之一如圖1所示。

G=G(V,E)E={E1,E2,E3,E4,E5},對圖進行點均勻著色劃分獨立集為{V1}{V2,V4}{V3}{V5}。在證明的過程中,我們關注的并不是找到這樣的具體劃分,而是確定是否存在獨立集元素數目一定的劃分。實際上,圖論著色方法可用于很多觀測矩陣具有統計結構相關性的情況下,該文所闡述的是均勻著色在觀測矩陣的有限等距特性證明的應用。其中著名的Hajnal-Szemerédi定理[9]：給定一個正整數r,如果一個圖G最大度不超過r,那么這個圖G存在一個均勻(r+1)-著色。

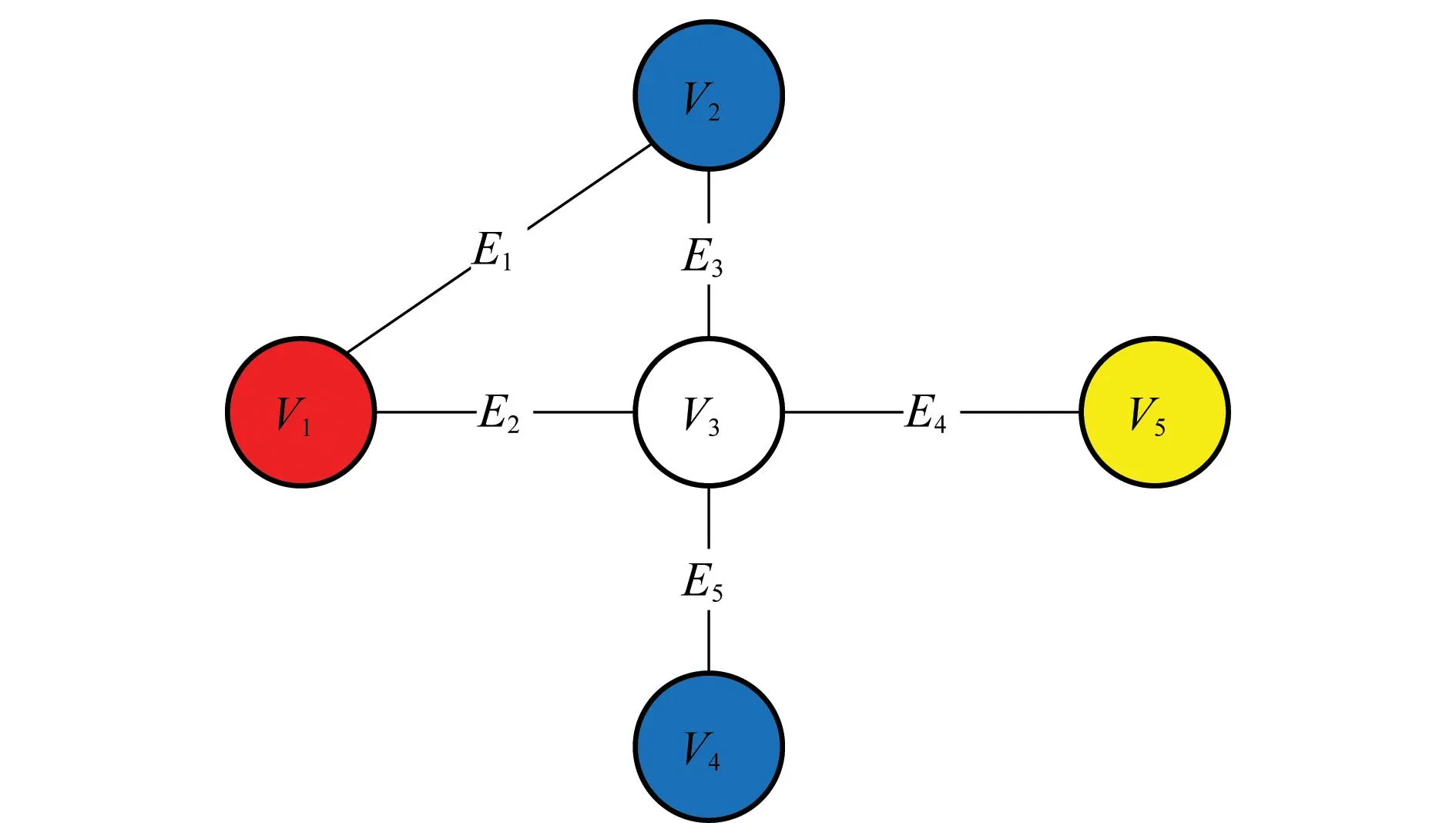
圖1　5階無向簡單圖均勻點著色示意圖

2Toeplitz矩陣RIP特性證明——圖論方法

通常,我們最常用的壓縮感知的理論模型為

(1)

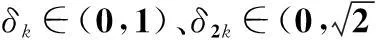
(2)

(3)

(4)

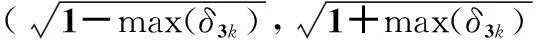
目前在多項式時間上,還沒有方法測試一個給定的觀測矩陣是否滿足RIP,能做的就是給定的觀測矩陣能以多大的概率滿足RIP。大多數的觀測矩陣理論研究都是圍繞高斯隨機矩陣而進行的,并且理論研究表明高斯隨機矩陣的效果確實不錯。在實際應用中,我們并不能主觀選擇觀測矩陣,觀測矩陣與感知過程的物理性質以及物理實現是有緊密聯系的。由于高斯隨機矩陣的物理實現較復雜或成本較高,實際的觀測矩陣通常不是高斯隨機矩陣,也不是伯努利隨機矩陣[11]。大量研究表明：Toeplitz矩陣由于可以通過離散傅里葉變換實現而受到廣泛關注。形式如下所示：

(5)

零均值高斯分布

(6)

零均值其他分布

(7)

定義 1對方陣L∈Cl×l,

行蓋爾圓盤為

(8)

列蓋爾圓盤為

(9)

引理 1(圓盤定理) 對方陣L∈Cl×l,L的特征值

(10)

定理 1給定k,n,在m≥c·kln(n/k)條件下,如果觀測矩陣Θ的項滿足上述若干獨立同分布之一,且對于任意的δ3k∈(0,1/3)和任意的T?{1,2,…,n}、|T|=3k,以高概率滿足RIP-3k約束,則根據索引列集合T而得到m×|T|的子矩陣將以大于1-e-f(m,k,δ3k)的概率滿足RIP-3k約束。

其中,f(m,k,δ3k) 是參數m,k和δ3k的實數函數。

如果θi服從同一獨立同分布,觀測矩陣Θ是m×n的Toeplitz矩陣,則對于任意的δ3k∈(0,1/3)和任意的T?{1,2,…,n}、|T|=3k,根據索引列集合T而得到m×|T|的子矩陣ΘT將以大于1-e-f(|m/q|,k,δ3k)+ln(q)的概率滿足RIP-3k約束。

其中q=3k(3k-1)+1。下面就給出定理1的證明過程。

證明根據文獻[13]有

(11)

式中

給定δ3k∈(0,1/3),T?{1,2,…,n}、|T|=3m。由ΘTi·(ΘTi·表示矩陣ΘT的第i行)中的共m行元素構造一個簡單無向圖G=G(V,E),V={1,2,…,m},E={(i,i′)∈V×V:i≠i′,ΘTi·和ΘTi′·是相關的}。由Toeplitz矩陣ΘT性質可得：ΘT的任一行最多與其他的|T|(|T|-1)=q-1行相關,也就是說,在構造的圖G中,某個頂點最多與q-1個頂點相鄰或者由某個頂點引出的邊最多有q-1條,用圖論的專業術語就是圖G的最大自由度Δ(G)≤q-1。由Hajnal-Szemerédi定理可知,圖G存在一個均勻q-點著色。我們用Cj表示某種顏色的頂點集合,即獨立集。則有

(12)

同時也可以得到

(13)

(14)

(15)

證畢

3Toeplitz矩陣RIP證明——蓋爾圓盤法

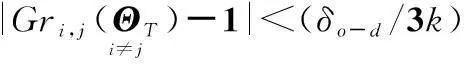
上文已經給出行蓋爾圓盤和列蓋爾圓盤的定義,下面給出蓋爾圓盤半徑定義。

定義 2對方陣L∈Cl×l,蓋爾圓的半徑定義為Gr(ΘT)蓋爾圓盤的中心

(16)

引理 2對方陣L∈Cl×l,它的全部特征值都位于以ci為中心,直徑為di=di(ci,ri)的圓盤內，ci=Li,i(i=1,2,…,l)。

3.1零均值高斯分布的Toeplitz矩陣RIP證明

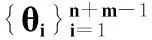
下面給出定理2的證明。

證明對角線元素的對稱約束我們有

(17)

對于獨立的非對角線元素,會比較復雜。首先將非對角線元素作變形有

(18)

當m是偶數時,式(18)可以改寫為

當m是奇數時,式(18)又可以改寫為

式中,t1,t2是重新組合的元素個數。π1,π2是組合算子,沒必要將組合算子π1,π2的構成弄清楚,只要知道存在這樣的組合算子即可。

將一個大的組合分成2個小組合,再應用對稱約束得

δo-d∈[0,1],應用大致估計t1≤t2≤m,可得

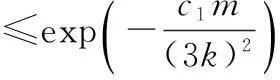
證畢

3.2零均值約束隨機分布的Toeplitz矩陣RIP證明

下面給出定理3的證明：

證明應用蓋爾圓盤定理,得Gram矩陣Gr(ΘT)的對角線元素和非對角線元素的對稱約束條件。

對角線元素的單對稱約束為

(19)

對角線元素的聯合對稱約束為

(20)

Gram矩陣Gr(ΘT)的非對角線元素可視為Toeplitz矩陣不同列的內積,以下例作為說明。

(21)

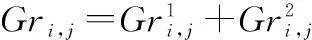
因此,非對角線元素的單對稱約束為

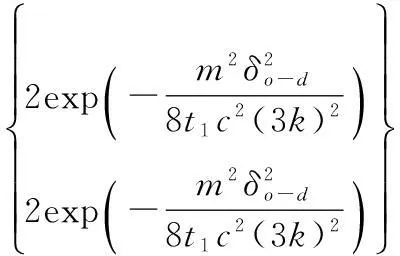
同樣應用大致估計t1≤t2≤m,可得

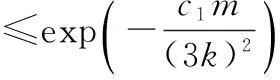
證畢

由于循環矩陣是特殊形式的Toeplitz矩陣,故上述證明對循環矩陣也適用。

4實驗仿真

實際的無線信道的稀疏性特性使得壓縮感知的重構算法應用于無線信道估計有了可能,本文將一種機器學習算法(稀疏貝葉斯學習算法[16](sparseBayesianlearning,SBL)應用于長期演進(longtermevolution,LTE)系統信道估計,比較了傳統的最小二乘算法(leastsquare,LS)、線性最小均方誤差(linearminimummeansquareerror,LMMSE)算法、高斯觀測矩陣的壓縮感知算法以及Toeplitz觀測矩陣的壓縮感知算法的均方誤差。系統仿真參數如表1所示,Matlab仿真結果如圖2所示。

表1　仿真參數

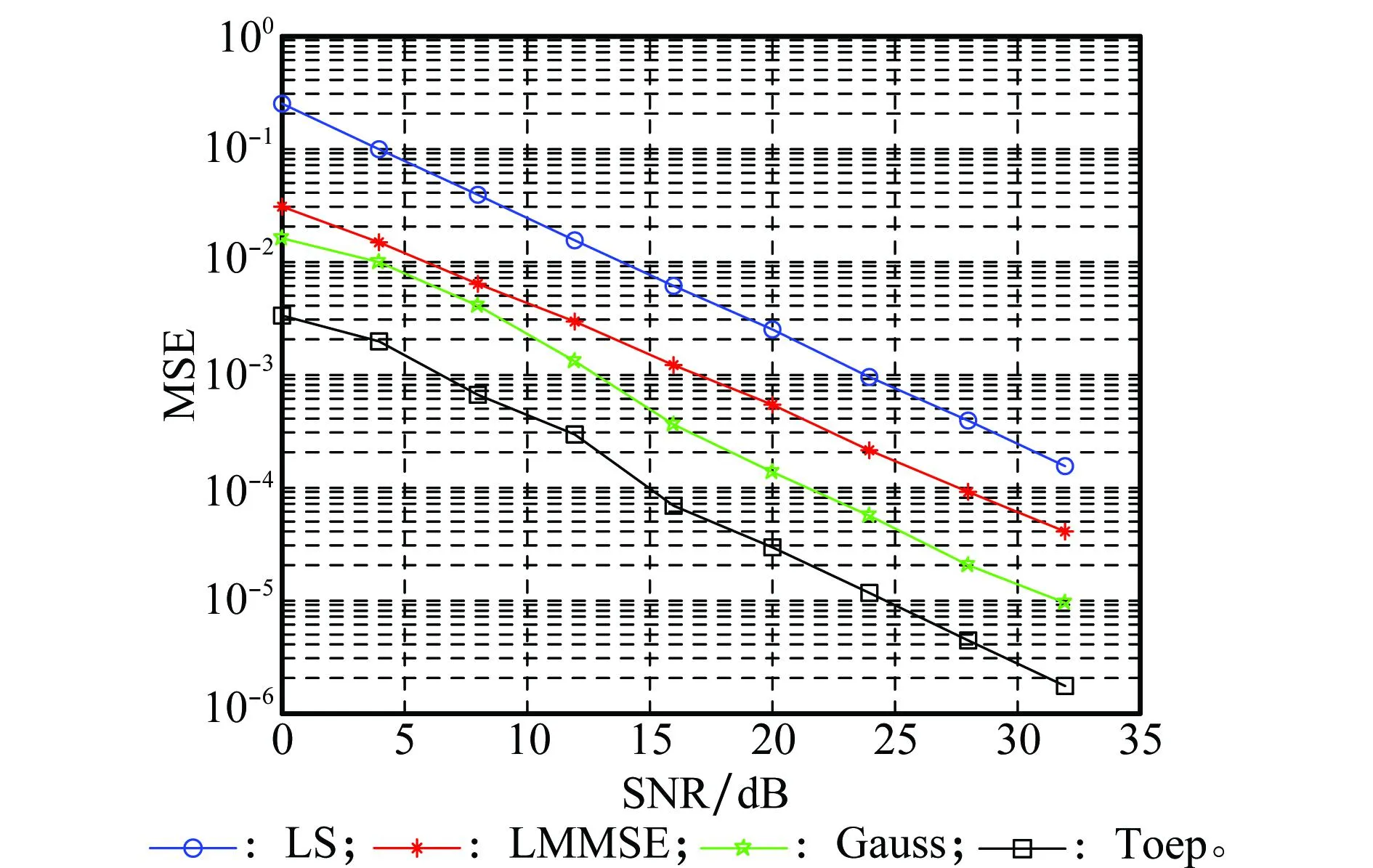
圖2　LS、LMMSE、Gauss、Toeplitz的信道估計均方誤差比較

高斯觀測矩陣和Toeplitz觀測矩陣的相關性, Gauss、Toeplitz算法二者的運行時間比較如表2所示。

表2　觀測矩陣相關性和運行時間比較

由仿真結果可知,稀疏貝葉斯學習算法的性能要優于傳統的信道估計算法,且信噪比越大,優勢更大。Toeplitz觀測矩陣的相關性較高斯矩陣而言更大,算法運行時間更短,均方誤差更小。

5總結

觀測矩陣的設計是壓縮感知三要素之一, 是將壓縮感知從理論推向實際應用的一個關鍵因素。傳統的高斯隨機矩陣雖然能很好地滿足RIP,但是其隨機特征導致物理實現困難。Toeplitz 隨機觀測矩陣由于可以使用快速傅里葉變換而在物理上實現更容易、 存儲成本更低。而該文引入圖論著色理論和蓋爾圓盤定理,證明了Toeplitz 隨機觀測矩陣以較大概率滿足RIP。同時實驗仿真表明,與高斯觀測矩陣比較而言,Toeplitz 觀測矩陣的運算復雜度和性能都優于前者,這對于 CS 理論的實際應用具有非常重要的意義。

參考文獻：

[1] Donoho D L．Compressed sensing[J].IEEETrans.onInformationTheory,2006, 52 (4):1289-1306.

[2] Candes E J, Tao T．Near-optimal signal recovery from random projections:universal encoding strategies[J].IEEETrans.onInformationTheory,2006, 52 (12):5406-5425.

[3] Candes E J, Tao T． Decoding by linear programming[J].IEEETrans.onInformationTheory, 2005, 51 (12):4203-4215.

[4] Cohen A, Dahmen W, DeVore R. Compressed sensing and bestk-term approximation[J].JournaloftheAmericanMathematicalSociety, 2009,22(1):211-231.

[5] Cen Y G, Zhao R Z, Miao Z J, et al. A new approach of conditions on δ2s(Φ)fors-sparse recovery[J].ScienceChinaInformationSciences, 2014, 57(4):1-7.

[6] Guédon O, Litvak A E, Pajor A,et al. Restricted isometry property for random matrices with heavy-tailed columns[J].ComptesRendusMathematique, 2014, 352(5):431-434.

[7] He X, Song R. Pilot pattern optimization for compressed sensing based sparse channel estimation in OFDM systems[C]∥Proc.oftheInternationalConferenceonWirelessCommunicationsandSignalProcessing, 2010:1-5.

[8] Chen B L, Lih K W, Yen C H. Equivalence of two conjectures on equitable coloring of graphs[J].JournalofCombinatorialOptimization, 2013, 25(4):501-504.

[9] Lo A, Markstr M K. A multipartite version of the Hajnal-Szemerédi theorem for graphs and hypergraphs[J].Combinatorics,ProbabilityandComputing, 2013, 22(01):97-111.

[10] Rauhut H, Romberg J, Tropp J A. Restricted isometries for partial random circulant matrices[J].AppliedandComputationalHarmonicAnalysis, 2012, 32(2):242-254.

[11] Strohmer T. Measure what should be measured:progress and challenges in compressive sensing[J].IEEESignalProcessingLetters, 2012, 19 (12):887-893.

[12] Haupt J, Bajwa W U, Raz G,et al. Toeplitz compressed sensing matrices with applications to sparse channel estimation[J].IEEETrans.onInformationTheory,2010,56(11):5862-5875.

[13] Krahmer F, Mendelson S, Rauhut H. Suprema of chaos processes and the restricted isometry property[J].CommunicationsonPureandAppliedMathematics, 2014.

[14] Rivenson Y, Stern A, Rosen J. Reconstruction guarantees for compressive tomographic holography[J].OpticsLetters, 2013, 38(14):2509-2511.

[15] Marsli R, Hall F J. Geometric multiplicities and Ger?gorin discs[J].TheAmericanMathematicalMonthly,2013,120(5):452-455.

[16] Prasad R, Murthy C R, Rao B D. Nested sparse Bayesian learning for block-sparse signals with intra-block correlation[C]∥Proc.oftheIEEEInternationalConferenceonAcoustics,SpeechandSignalProcessing, 2014:7183-7187.

陳忠輝(1960-),男,教授,碩士，主要研究方向為通信系統、信號處理。

E-mail：czh@fzu.edu.cn

熊蕓(1988-),女,碩士研究生,主要研究方向為無線通信、壓縮感知、信道估計。

E-mail：liuyunnima0911@gmail.com

網絡優先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20141105.1646.018.html

Research on the restricted isometry property for Toeplitz matrix

CHEN Zhong-hui, XIONG Yun

(CollegeofPhysicalandInformationEngineering,FuzhouUniversity,Fuzhou350116,China)

Abstract:The restricted isometry property (RIP) of the sensing matrix has recently received a lot of attention under the rubric of compressive sensing. Most studies have shown that a Gaussian random sensing matrix satisfies the RIP in theory. However, due to its high cost of storage and complex physical implementation, the Toeplitz sensing matrix is more in favored than the Gauss sensing matrix in actual. Because it can be implemented by the fast discrete Fourier transform. Proof of the RIP for the sensing matrix exploiting graph theory and the Ger?gorin’s disc theorem is given. The results show that the Toeplitz random matrix satisfies the RIP with high probability. And the least square (LS), linear minimum mean square error (LMMSE), compressive sensing algorithm with the Gauss sensing matrix and compressive sensing algorithm with Toeplitz sensing matrix channel estimation algorithm are compared. The simulation results show that the Toeplitz sensing matrix has a superiority over the Gauss sensing matrix on computation complexity and the traditional channel estimation method on performance and computation complexity. It provides a theoretical and realistic foundation for reconstructing the original signal losslessly.

Keywords:sensing matrix; restricted isometry property (RIP); equitable coloring; Ger?gorin’s disc theorem

作者簡介：

中圖分類號：TN 919.5

文獻標志碼：ADOI:10.3969/j.issn.1001-506X.2015.05.07

基金項目：國家自然科學基金(61170147)；福建省教育廳科技項目(JA12024)資助課題

收稿日期：2014-06-26；修回日期：2014-08-31；網絡優先出版日期：2014-11-05。