大中華區股市波動的相關性及動態聯動性研究

楊桂元，羅 陽，方媛媛

（安徽財經大學 數量經濟研究所，安徽 蚌埠 233030）

0 引言

隨著國際金融一體化，每一個股票市場并不是獨立運行的個體，由于世界各地的經濟聯系日益增強，以及一地區企業在其他地區股票市場交叉上市等因素的影響，各地股票市場是相互聯系的。由此，一個地區的股市都會或多或少與其他地區的股市之間存在相關性以及聯動性。

而大中華區中的中國大陸、香港和臺灣地區的股票市場中，臺灣和香港的股票市場有著比大陸更長的發展歷史。隨著香港回歸，大陸股票市場的逐步成熟以及證券市場的逐步開放，2008年以來兩岸積極的經濟政策等因素的影響，大陸股市和香港、臺灣股市之間的聯系也在逐漸增強。由此，對大中華區四個股市關系的準確把握，這對于投資者構造多樣化投資組合，以及區域內相關部門政策的制定，都是非常有必要的。

本文用多元對角VECH-GARCH模型分析整個大中華區四個股市之間的相關關系，用多元DCC-GARCH模型分析它們之間的動態聯動性。以完善大中華區股市間相關性的研究。

1 GARCH模型族理論及相關波動性理論

1.1 多元對角VECH-GARCH模型及波動的相關性介紹

（1）股市間波動的相關性介紹

一個股票市場可能受自身的影響而產生波動，也可能會受別的股市波動的影響而產生波動。對于這種相關關系，常用的方法是對資產收益率的條件方差和條件協方差進行建模，來刻畫各金融市場間的波動相關性，而多元對角VECH-GARCH模型在分析這種相關性具有重要的作用。它的方差方程中，既包含各自變量的單項GARCH方差，也包含它們之間的協方差。以此來判定這些變量之間的大致相關關系。

（2）多元對角VECH-GARCH模型

設ut表示一個k×1維隨機向量序列，且有ut|Yt-1服從N(0，Ht)分布，Yt-1是到t-1時刻的信息集，Ht是k階正定矩陣。Bollerslev（1988）提出了一個一般的條件協方差多變量VECH模型的限制形式。均值方程為：

方差方程為：

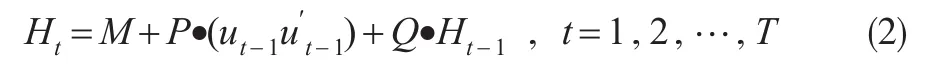
式中：算子“·”表示兩個矩陣的元素與元素乘積（Hadamard算子）。系數矩陣M、P和Q都是k階的對稱矩陣。可以利用不同的方式確定系數矩陣的參數，本文采用的是無限形式（Indefinite Matrix）：

向量ARCH類模型主要是研究Ht的不同動態特性。確定參數的最常用的方式是允許矩陣中的參數無限制的變化，即用無限制矩陣來確定參數。模型可以構造如下：

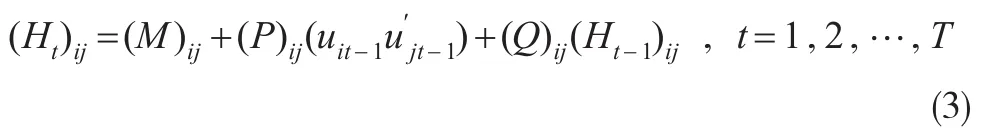
式中(Ht)ij就是矩陣Ht中的第i行，第j列元素。因為系數矩陣M、P和Q都是k階的對稱矩陣，式(3)中的每個矩陣包含了k(k+1)/2個參數。

以二元對角VECH模型為例，令矩陣M為方差方程中常數項的系數矩陣，矩陣P為方差方程中ARCH項的系數矩陣，矩陣Q為方差方程中GARCH項的系數矩陣(因為系數矩陣M、P和Q都是對稱矩陣，式(3)中的每個矩陣包含了2×(2+1)/2=3個參數)。方差方程可以表示為：

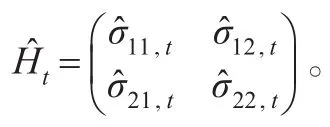
三個系數矩陣的估計結果分別為：

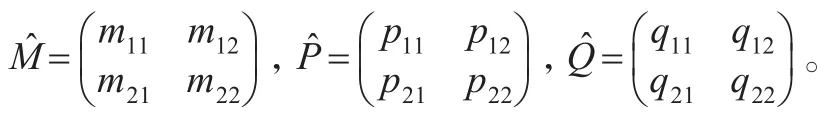
矩陣P?的各個元素表示了各變量的上一期殘差的平方之間相互影響，而矩陣Q?的各個元素則表示了各變量的上期方差和協方差之間的相互影響關系。寫成方程形式，則方差方程為：

第一個變量的方差方程：

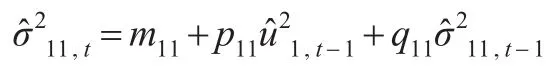
第二個變量的方差方程：

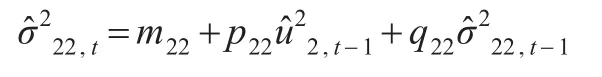
這兩個方程中，滿足約束條件每個方程的上期殘差平方項和方差項的系數之和都小于1。

條件協方差方程：

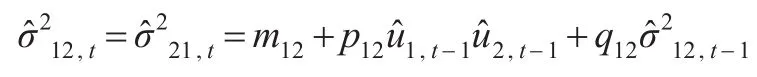
1.2 多元DCC-GARCH模型及波動的聯動性介紹

（1）股市間波動的聯動性介紹

股票市場的聯動性，指股票市場之間存在著明顯的收益率波動的關聯性，即一個股票市場產生波動，會引起另外一個股票市場的變動。相關系數是解釋金融市場之間聯動效應的一個很重要指標，而且市場間的相關系數并不是靜態固定不變的，是隨時間發生變化的，DCC-GARCH模型正是分析動態相關關系的重要模型。

（2）多元DCC-GARCH模型

Engle(2002)提出了DCC-GARCH模型，它是常條件相關系數(CCC-GARCH模型)的進一步拓展。與其他多元GARCH模型一樣，可以克服異方差性的影響。可以用來估計多個資產之間的動態相關關系。

設k種資產收益rt服從均值為0，協方差矩陣為Ht的多元正態分布。

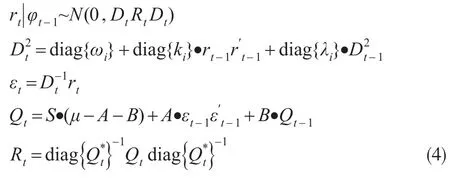
其中，φt-1為截止到t-1時期所有可能獲得的信息集合；是一個對角矩陣，對角線上的元素為各單變量的條件方差；S為標準化殘差εt的無條件協方差矩陣；Rt為條件相關系數矩陣；符號“·”表示矩陣對應元素的點乘；Qt為標準化殘差的條件協方差矩陣；為對角矩陣，對角線元素是Qt對角元素的平方根。

模型的參數采用最大似然估計，估計過程分兩步進行。首先對各個單變量分別進行GARCH模型得出個單變量的條件方差和殘差序列。之后利用條件方差標準化殘差序列估計多元DCC-GARCH模型的條件相關系數矩陣Rt。根據Rt來分析大中華區股市的聯動性。

2 實證檢驗

2.1 數據的選取

在分析股市間的相關性及傳遞性時，本文首先分別選取上證綜合指數、深圳成分指數、香港恒生指數、臺灣加權指數的日收盤價格指數2006年1月4日至2013年2月28日的數據。再計算其收益率，公式為：

其中i取1、2、3、4分別表示上海、深圳、香港、臺灣股市。Ri，t為i市場的收益率序列，Pi，t表示第i市場第t日的收盤價。即分別用上海綜指收益率{RSH}、深圳成指收益率{RSZ}、香港恒生收益率{RHK}、臺灣加權收益率{RTW}作為變量來進行建模分析。

由于大陸、香港、臺灣的節假日不同，需要把數據對齊。選取四個股市都開盤的交易日，剔除掉有股市不開盤的交易日的收益率數據，共1649組數據。以此得到的收益率數據，來分析股市間的相關性及傳遞性。

2.2 對各收益率序列統計分析及ARCH效應檢驗

大中華區各股市收益率序列的時序圖如圖1所示。從時序圖中可以很直觀的看出，各股市收益率序列都出現波動率的聚集現象，即方差在一定時段中比較小，而在另一時段中比較大。

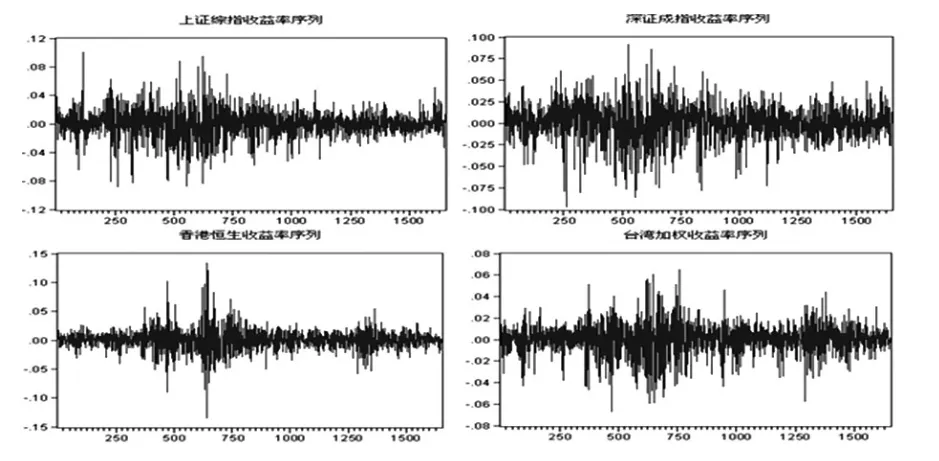
圖1 大中華區股票市場收益率序列時序圖

大中華區各股市收益率序列的描述性統計如表1所示，由J-B統計量可知，在1%的顯著水平下，四個股市的收益率序列都顯著不服從正態分布；由偏度值可知，上證綜指、深圳成指、臺灣加權指數都呈左偏態勢，香港恒生指數呈右偏態勢；四個股市的收益率序列的峰度值都明顯大于3，尖峰特征非常明顯。因此，大中華區各股市收益率序列分布都呈現出明顯的尖峰厚尾現象。

如果對非平穩時間序列進行建模，往往會出現虛假回歸問題。所以對這四個收益率序列進行建模之前，需要先對它們進行平穩性檢驗。本文分別選用ADF平穩性檢驗和PP平穩性檢驗。檢驗結果如表2所示。

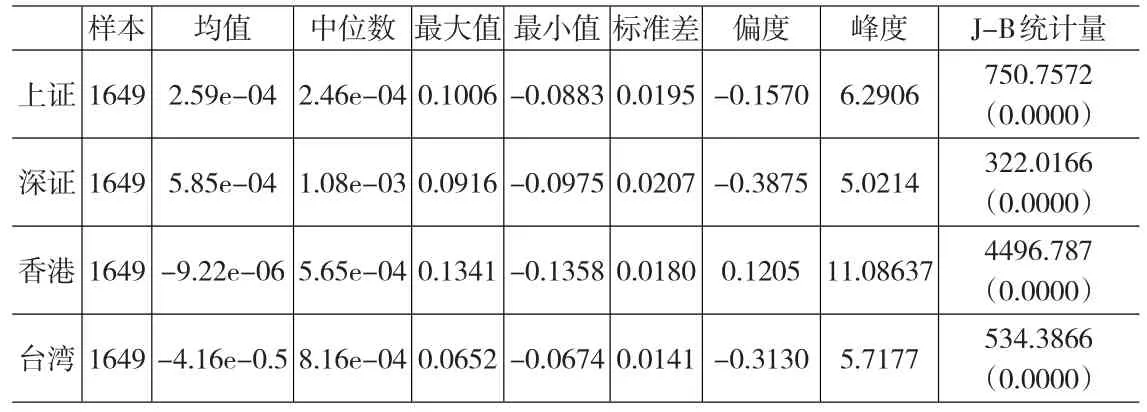
表1 收益率序列基本統計特征

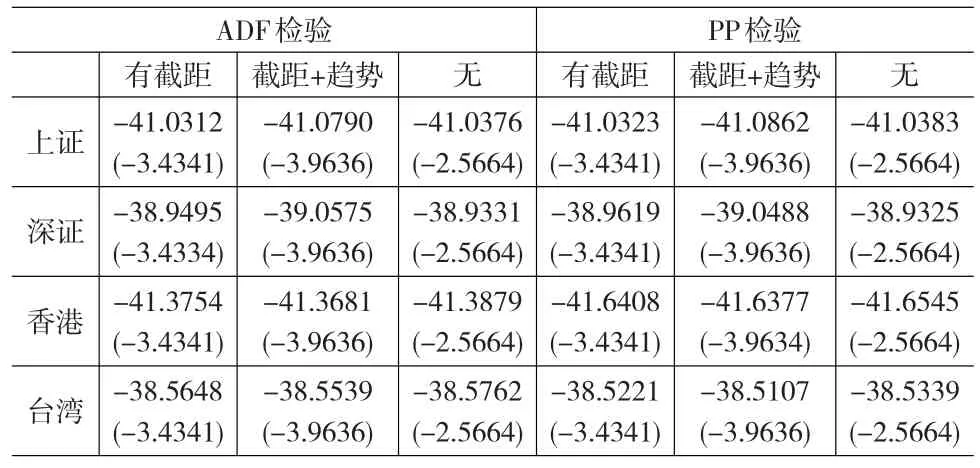
表2 收益率序列平穩性檢驗

由檢驗結果可知，在1%顯著水平下，只含有截距項、截距項加趨勢項、不包含截距項與趨勢項的任何形式的平穩性檢驗，ADF平穩性檢驗和PP平穩性檢驗都拒絕了這四個收益率序列有一個單位根的零假設。說明大中華區各股市收益率序列是平穩的，可以直接對它們進行建模。

收益率序列的自相關性確定均值方程；收益率的平方序列相關性確定是否存在非線性相關性，波動集聚現象是否明顯。其序列相關性檢驗及ARCH-LM檢驗結果如表3所示。

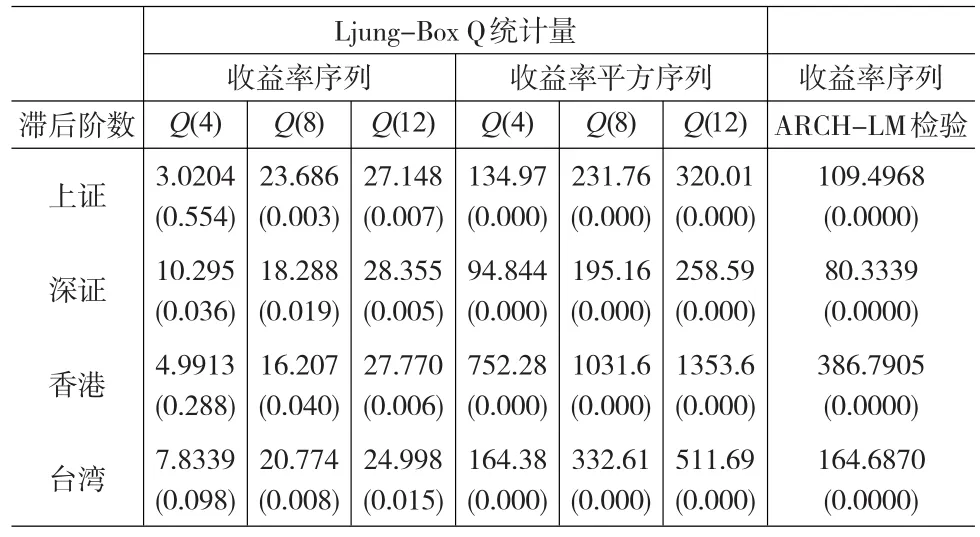
表3 收益率序列及收益率平方序列的相關性檢驗及ARCH-LM檢驗

由表3可知，在5%顯著水平下，上海，香港，臺灣股市收益率序列短期不存在自相關性，而長期都存在自相關。深圳股市收益率序列不管長短期都存在著自相關。收益率平方序列的Q統計量不管長期還是短期，大中華區各股市都非常顯著，表明這四個收益率序列存在著非線性自相關。且由ARCH-LM結果可知，四個收益率序列都存在異方差的特性，因此考慮建立多元GARCH模型。

2.2.1 基于對角VECH-GARCH模型的相關性分析

利用上證綜指、深證成指、香港恒生指數、臺灣加權指數收益率數據兩兩建立二元GARCH(1,1)模型，在估計過程中，選擇的模型類型為對角VECH模型。其中建立上海-深圳股市VECH模型的均值方程中，上海股市自變量有rsh(-2)，深圳股市自變量有rsz(-1)；建立上海-香港股市VECH模型的均值方程中，上海股市自變量有rsh(-6)，香港股市自變量有rhk(-6)；建立深圳-香港股市VECH模型的均值方程中，深證股市自變量有rsz(-1)，香港股市自變量有rhk(-10)；建立上海-臺灣股市VECH模型的均值方程中，上海股市自變量有rsh(-6)，臺灣股市自變量有rtw(-1)；建立深圳-臺灣股市VECH模型的均值方程中，深圳股市自變量有rsz(-6)，臺灣股市自變量有rtw(-1)；建立香港-臺灣股市VECH模型的均值方程中，香港股市自變量有rsh(-1)，臺灣股市自變量有rsz(-1)。

均值方程不是本文關注的重點，而可以從方差方程得出兩個股市間的相關關系，所以本文重點列出方差方程的估計結果。對于滬、深、港、臺之間的VECH模型的方差方程結果如表4所示。

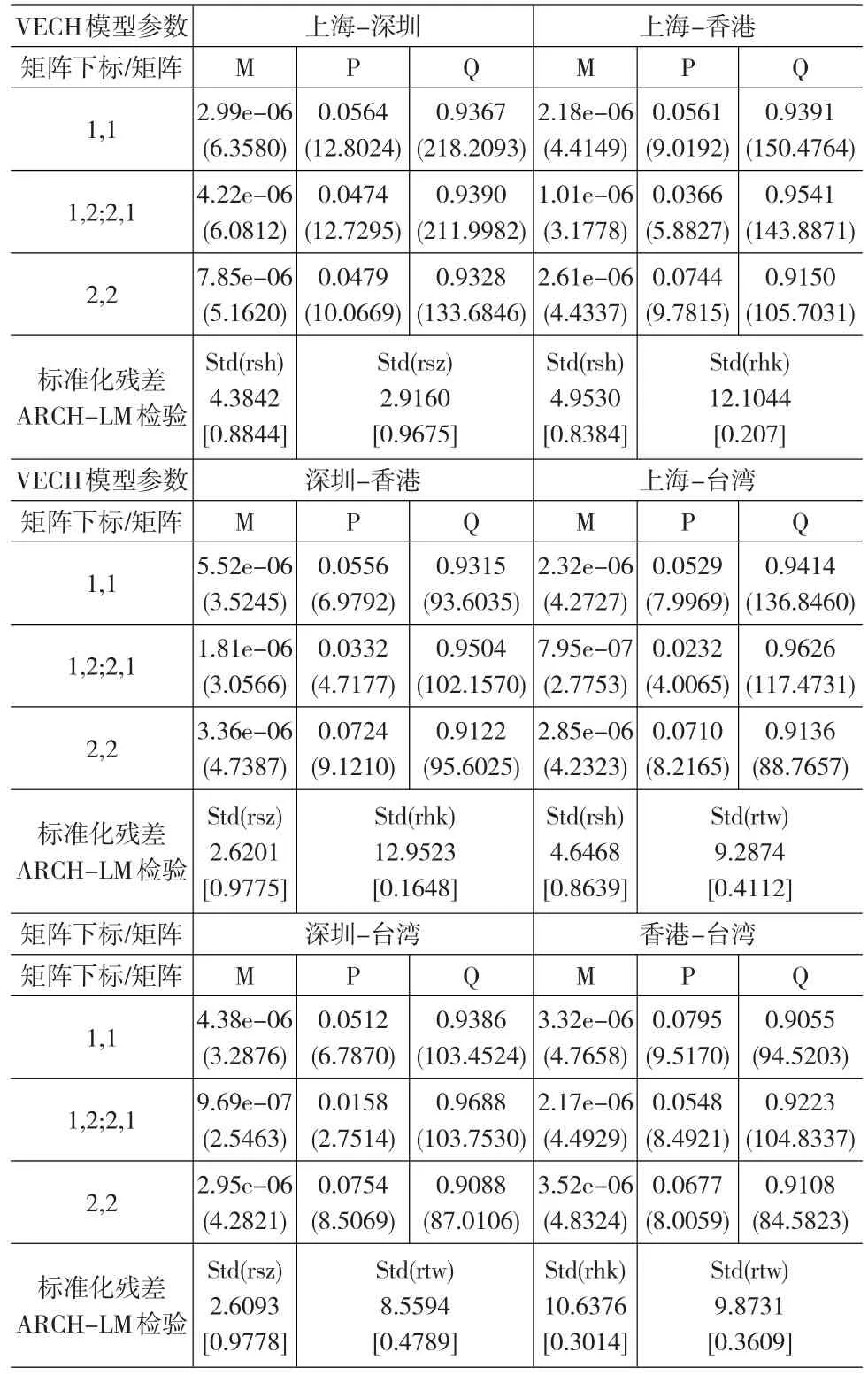
表4 滬深港股市間的VECH模型估計結果

為保證建立的模型正確，需要對模型的殘差進行必要的檢驗，由表4可知，標準化殘差都接受了ARCH-LM檢驗的原假設，表明各殘差都不存在ARCH效應(異方差性)，說明模型的建立是合理的。

在以上方程參數中，每個方程的上期殘差平方項Pii，i=1，2 和方差項Qii，i=1，2 的系數之和都小于1，滿足約束條件，并且系數之和都接近1，表明收益率序列受到沖擊時，其影響存在著較為長久的ARCH效應（異方差）。

2.2.2 基于多元DCC-GARCH模型的聯動性分析

股市之間的聯動現象是國際證券市場中的一個十分重要的經濟現象。對于某個地區的股票市場而言，周邊地區股票市場和國際金融市場的宏觀經濟走勢的沖擊，將會改變市場之間原有的聯動性，帶來新一輪的聯動效應。國際股票市場關聯以股票市場的一體化和經濟一體化為基礎和依托。本文以動態相關系數來考查大中華區股市間的聯動現象。如果不考慮大中華區股市收益率之間的動態關系，計算它們之間的非條件相關系數，其結果如表5所示。

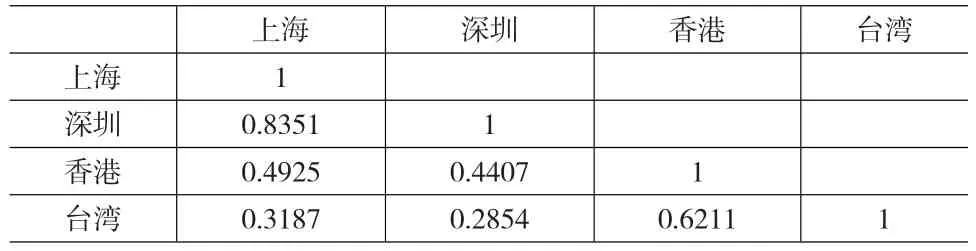
表5 大中華區各股市間的無條件相關系數

由表5可知，上海股市與深圳股市的相關程度最高，為0.8351。盡管可以從相關系數中看出他們之間的相關程度，但是這些系數都是靜態的，不能反應他們相關系數的變化過程。所以考慮建立DCC-GARCH模型，以觀察他們之間的相關性隨時間變化的過程。

建立DCC-GARCH模型，分兩步進行，首先建立各單變量的GARCH模型，其結果如表6所示。

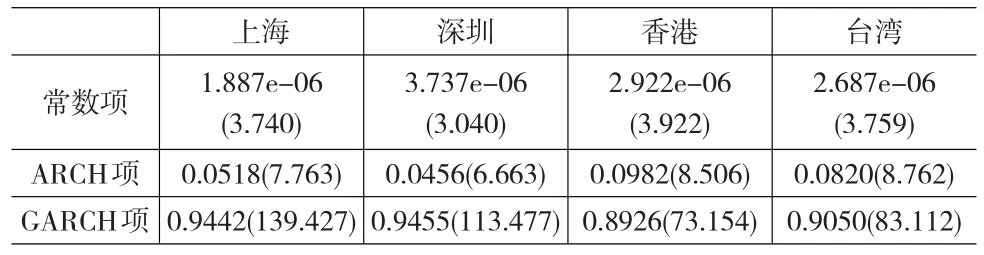
表6 對各單變量建立GARCH模型結果

由表6可知，大中華區股市的ARCH項系數與GARCH項系數之和都均小于1，滿足參數約束條件，且非常接近于1，表明各股市所受的波動沖擊是持續和持久的。

之后利用條件方差標準化殘差序列兩兩估計多元DCC-GARCH模型的參數Rt。經檢驗，標準化殘差都接受了ARCH-LM檢驗的原假設，表明各殘差都不存在ARCH效應，模型的建立是合理的。根據DCC-GARCH模型的Rt，得出大中華區股市的動態相關關系圖，如圖2所示。

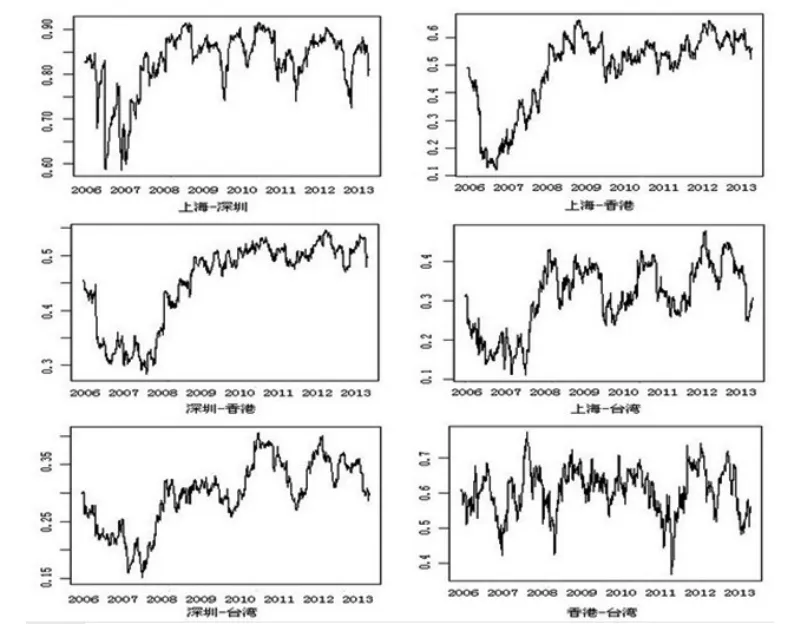
圖2 大中華區股票市場收益率序列的動態相關關系圖

由圖2可知，上海股市與深圳股市的相關程度相當高，從2007年開始相關系數有顯著提高，從0.6到0.7之間增加到0.85左右，并維持在此水平上下波動。這是因為2006年中國大陸基本完成股改以后，市場健康穩定運行的內在基礎不斷夯實，市場的投資價值正在逐步為投資者所關注，資本市場已經初步具備了實現重要發展突破的基本條件。這對滬深股市相關性的增強有著密切關系。

上海股市、深圳股市與香港股市的相關性，也是從2006年中國大陸基本完成股改之后，2007年開始分別從0.2和0.3左右上升到0.5～0.65和0.5～0.6之間，在此區間上下波動。由此我們發現，2006年基本完成股改之后，我國股市之間及與香港股市之間相關性都有著顯著的提高，說明股改對我國的股市發展有著積極的意義。

上海股市、深圳股市與臺灣股市的相關性，在2006～2008年間一直處于下降狀態，而2008年之后，大陸股市與臺灣股市的相關性有所增強，它們之間的相關系數從0.2左右分別上升到0.3～0.4之間及0.3～0.35之間，并在此區間上下波動。這可能與2008年馬英九當選臺灣領導人之后，兩岸局勢發生積極變化，兩岸關系迎來難得歷史機遇。兩岸同胞往來之頻繁、經濟聯系之密切、文化交流之活躍、共同利益之廣泛是前所未有的。這是導致兩岸股市的相關性增強的主要原因。

香港股市與臺灣股市的相關系數從2006～2013年間，都是維持在0.6左右上下波動，這說明香港股市與臺灣股市開市比較早且成熟，相關程度也比較穩定。其中，從2006～2013年間，共有三次重大波動。這可能是受國際股市的影響，2007年美國爆發金融危機以來香港與臺灣股市的相關系數出現了第一次大的波動；到2008年8月，美國房貸兩大巨頭——房利美和房地美股價暴跌，持有“兩房”債券的金融機構大面積虧損，香港與臺灣股市的相關系數出現了第二次大的波動；2011年美國爆發了美債危機，導致香港與臺灣股市的相關系數出現了第三次大的波動。由此可見，香港和臺灣股市受國際股市的影響較大。

3 結束語

本文在回顧多元GARCH類模型的基礎上，用多元對角VECH-GARCH模型以及多元DCC-GARCH模型分析它們之間的相關性和動態聯動性，分析結果表明：大中華區的日收益率波動的條件方差之間的相互影響是持久的，在世界經濟全球化背景下，大中華區股市的波動呈現出趨同的現象；2006年中國大陸基本完成股改以后，滬深股市相關性有明顯的增強；而且我國股市之間及與香港股市之間相關性都有著顯著的提高，說明股改對我國的股市發展有著重要的意義；2006年的股改基本完成和2008以來積極的兩岸政策，導致兩岸股市的相關性明顯增強；而香港和臺灣股市的相關性受國際股市的影響較大。

由此可見，我國有關部門應當不遺余力的落實和完善股改政策，積極發展對臺灣的經濟政策，加強兩岸的金融交流。而且應當及時關注外部市場環境和需求的變化，有針對性的進行市場結構調整，建立健全產品體系，進一步加快金融產品的研發和創新，促進我國股票市場朝著高效安全、結構合理、功能完備的方向健康有序發展，為更好地服務國民經濟，做出應有的積極貢獻。

[1]樊智,張世英.多元GARCH建模及其在中國股市波動分析中的應用[J].管理科學學報,2003,6(2).

[2]谷耀,杜麗娜.滬、深、港股市信息溢出效應與動態相關關系—基于DCC-(BV)EGARCH-VAR的檢驗[J].數量經濟技術經濟研究,2006,8(1).

[3]董秀良,吳仁水.基于DCC-MGARCH模型的中國A、B股市場相關性及解釋[J].中國軟科學,2008,(7).

[4]王鷹翔,張魯欣.基于向量GARCH模型的國際證券市場波動溢出研究[J].管理評論,2011,(6).

[5]Robert F，Engle.Dynamic Conditional Correlation:A Simple Class of Multivariate Generalized Autoregressive Conditional Heteroskedasticity Models[J].2002,20(3).

[6]將治平.人民幣利率與匯率的動態相關關系：基于DC C模型的研究計量經濟分析方法與建模[J].軟科學,2008,22(7).