空間直角坐標轉換的統一模型

吳繼忠 王安怡

1 南京工業大學測繪學院，南京市浦珠南路30號，211816

2 大連海洋大學海洋與土木工程學院，大連市黑石礁街52號，116023

根據空間維數的不同，空間直角坐標轉換一般分為二維平面和三維空間坐標轉換。二維平面坐標轉換可直接變換成線性模型，其解算過程容易實現。三維空間直角坐標轉換中，在旋轉角度很小的情況下可以對旋轉矩陣作一定的近似處理，從而轉化為線性模型進行求解。當旋轉角為大角度時，在小范圍測區內7參數之間存在強相關性［1］，更難以處理的是旋轉矩陣的各個參數關系復雜，通常進行線性化或迭代運算［2－3］進行求解，這些方法在實際應用中均有一定的條件限制或者使用復雜。本文提出了空間直角坐標轉換的統一模型，結合空間直角坐標轉換中旋轉矩陣的正交特性，將模型求解轉換為正交Procrustes問題，實現了二維和三維空間直角坐標轉換的直接線性解算。

1 空間直角坐標轉換的數學模型

二維平面坐標轉換模型可以表示為：

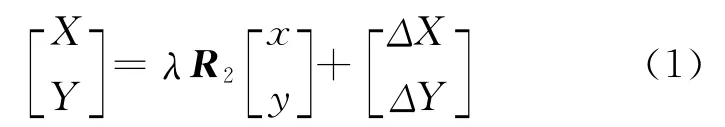
式中，λ為尺度參數；為平移參數；旋轉矩陣，φ是旋轉角。顯然，R2是正交矩陣，滿足

三維空間直角坐標的轉換模型表示為：

式中，λ為尺度參數；為平移參數；，其中為3個軸向旋轉對應的旋轉矩陣，其構成可參見相關文獻，均為正交矩陣，因此R3也是正交矩陣，滿足

對比式（1）和式（2）可知，二維平面坐標轉換可以看成是三維空間直角坐標轉換的一種特殊形式，二者性質完全相同，區別僅在于矩陣的維數不同。以三維空間直角坐標轉換為例，設兩套坐標系的公共點數目為m，各點在不同坐標系下的坐標記為：

B為公共點在目標坐標系統下的坐標，A為公共點在原坐標系統下的坐標。顯然，每個公共點均滿足式（2）的條件，將第i（i＝1，2，…，m）個點代入式（2）并將左右兩邊矩陣進行轉置可得：

其中J＝［1，1，…，1］T為m×1的常數向量。由上述分析，空間直角坐標轉換的統一模型可寫為如下形式：

式中，k為常量，當k＝2或3時分別對應二維平面坐標轉換和三維空間直角坐標轉換，m為轉換中公共點的數目，R∈Rk×k是轉置后的旋轉矩陣，是滿足正交特性的方陣。式（6）即為空間直角坐標轉換的統一模型。

2 正交Procrustes分析

利用公共點求解轉換參數實際是要求出參數λ、R、T，使得λAR＋JT盡可能接近B，即求解如下問題：

其中‖·‖F表示Frobenius范數，R滿足RTR＝I，式（7）本質上屬于正交Procrustes問題。正交Procrustes問題可表述為：給定矩陣A∈Rn×p，B∈Rn×q，其中n＞q，求正交矩陣R∈Rp×q滿足‖AR－B‖F＝min。

根據正交Procrustes分析的解算方法［4］，針對式（6）的求解過程如下：記ε＝λAR＋JT－B，根據Lagrange原理構造極值函數：

式中，L為乘數因子矩陣。將式（8）分別對λ、R、T求偏導數：

由式（11）可得：

由式（10）左乘RT得：

由于RTATAR和（L＋LT）／2均是對稱矩陣，RTATB－RTATJTT也必須是對稱矩陣，即

將式（12）代入式（14）得：

將上式展開，根據對稱矩陣的特點同理可得：

記D＝AT（I－JJT／m）B，要使式（16）成立，必須

滿足：

將式（17）分別左乘R、右乘RT，得：

將式（18）左右相乘得：

將D進行奇異值分解，svd（D）＝UΣVT，其中U和V均為正交矩陣，代入式（19）得：

故旋轉矩陣R＝UVT，將式（12）代入式（9）得：

將R、λ代入式（12）即可得到平移參數T。根據旋轉矩陣R的展開式，可以反算出不同軸向上的旋轉角，其過程不再贅述。最后用單位權中誤差來評定精度，單位權中誤差計算公式為：

式中，ε＝λAR＋JT－B；f為自由度，在二維轉換和三維轉換的情況下分別等于2m－4和3m－7，m為公共點數量。

在計算過程中，首先將公共點坐標按式（6）構建矩陣A、B和常量矩陣J，再根據A、B、J構建矩陣D＝AT（I－JJT／m）B。對矩陣D進行奇異值分解，依次計算得到旋轉矩陣R、尺度參數λ和平移參數T，最后進行精度評定。

3 算例分析

3.1 算例1

以文獻［5］中的數據為例，5 個公共點在WGS－84和獨立坐標系下的坐標如表1所示。為便于比較，取1、2、3號點求轉換參數，再利用轉換參數將4、5號點轉換到地方坐標系，并與其已知值進行比較。

表1 平面坐標轉換公共點坐標Tab.1 Cartesian coordinates of common points

利用本文模型和方法，首先計算出旋轉矩陣，得到的旋轉角為359°01′20.575 4″，進一步得到尺度因子為3.064 875×10－6，最后由旋轉矩陣和尺度參數得到平移參數Δx＝－2 465 635.256 m，Δy＝－433 223.055m。利用上述轉換參數將4、5號點轉換到地方坐標系，結果見表2。

表2 平面坐標轉換公共點坐標Tab.1 Cartesian coordinates of common points

由表2可知，本文計算結果與已知結果間僅存在微小的差異，最大坐標較差為3 mm。造成這一差異的原因是點位坐標是實測結果，均包含一定的觀測誤差。

3.2 算例2

以4個點的三維空間直角坐標為原始坐標，模擬10 套不同轉換參數（表3），利用式（2）將4個控制點的原始坐標轉換到目標坐標系下，最后利用本文算法計算出轉換參數并與其模擬的真值進行比較，得出各個轉換參數的計算誤差及轉換參數求解的中誤差，結果列于表4。表4 最后一列為各個方案計算轉換參數的中誤差。

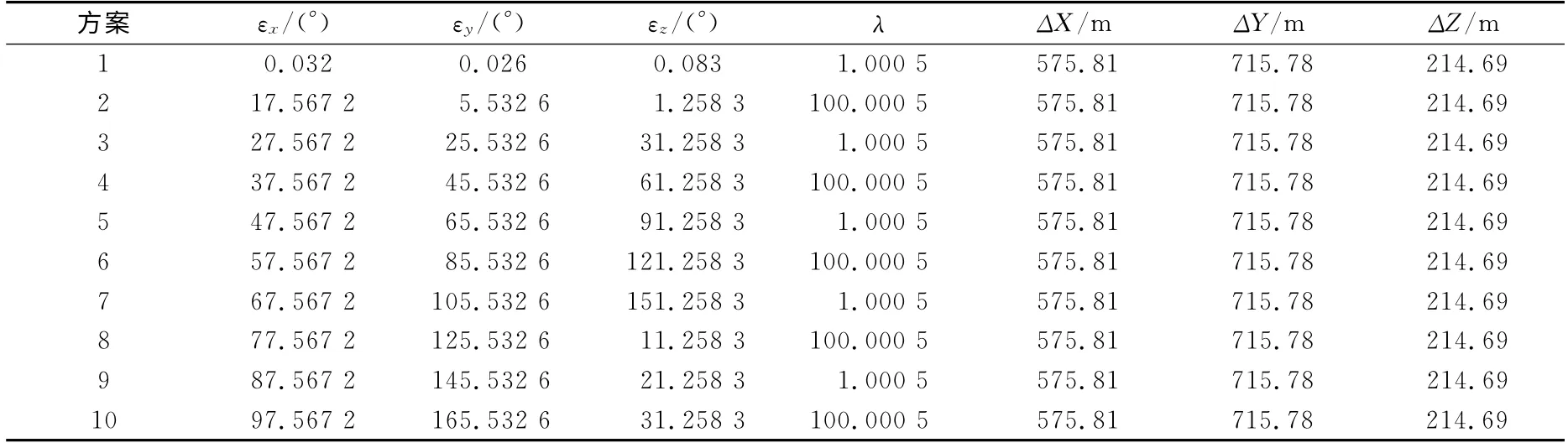
表3 模擬參數Tab.3 Simulation parameters and solutions

表4 模擬參數的求解誤差Tab.4 Errors of simulation parameters

從表4可以看出，本文計算方法對旋轉角、尺度參數和平移參數的數值范圍沒有限制，因而適合于任意條件下的三維空間直角坐標轉換。其計算過程為矩陣運算，是一種純粹的線性計算，突破了以往三維坐標轉換方法中對旋轉角的限制及計算方法的瓶頸問題，實現了三維坐標轉換的直接解算。由于模擬數據的點位坐標不存在誤差，在不同方案中，旋轉角的計算誤差小于10－13，尺度參數計算誤差小于10－14，平移參數計算誤差小于10－8，計算中誤差的數量級也在10－8以下，這些計算誤差是計算機運算過程中數據截斷誤差的累計所造成的，其大小對實際應用而言完全可以忽略不計。

4 結 語

本文提出了空間直角坐標轉換的統一方法。首先建立二維平面坐標轉換和三維空間直角坐標轉換的統一模型，采用正交Procrustes分析對模型進行解算。解算過程不需要參數的先驗近似值，也不需要線性化處理和迭代計算，對轉換參數的數值范圍沒有限制，實現了空間直角坐標的轉換在表示模型和解算方法上的統一。

［1］王解先.七參數轉換中參數之間的相關性［J］.大地測量與地球動力學，2007，27（2）：43－46（Wang Jiexian.Correlations among Parameters in Seven－Parameter Transformation Model［J］.Journal of Geodesy and Geodynamics，2007，27（2）：43－46）

［2］曾文憲，陶本藻.三維坐標轉換的非線性模型［J］.武漢大學學報：信息科學版，2003，28（5）：566－568（Zeng Wenxian，Tao Benzao.Non－Linear Adjustment Model of Three－Dimensional Coordinate Transformation［J］.Geomatics and Information Science of Wuhan University，2003，28（5）：566－568）

［3］姚宜斌，黃承猛，李程春，等.一種適用于大角度的三維坐標轉換參數求解算法［J］.武漢大學學報：信息科學版，2012，37（3）：253－256（Yao Yibin，Huang Chengmeng，Li Chengchun et al.A New Algorithm for Solution of Transformation Parameters of Big Rotation Angle’s 3D Coordinate［J］.Geomatics and Information Science of Wuhan University，2012，37（3）：253－256）

［4］Crosilla F，Beinat A.Use of Generalised Procrustes Analysis for the Photogrammetric Block Adjustment by Independent Models［J］.ISPRS Journal of Photogrammetry ＆ Remote Sensing，2002，56（2）：195－209

［5］姚宜斌.平面坐標系統相互轉換的一種簡便算法［J］.測繪信息與工程，2001（1）：1－3（Yao Yibin.A Simple and Convenient Arithmetic for the Transformation of Plane Coordinate System［J］.Journal of Geomatics，2001（1）：1－3