關(guān)于等價(jià)無(wú)窮大量代換求極限的補(bǔ)充

李紅菊，丁 健

(安徽新華學(xué)院公共課教學(xué)部，合肥230088)

0 引言

極限理論是微積分學(xué)說(shuō)的基礎(chǔ)，求函數(shù)的極限也是學(xué)生學(xué)習(xí)中常見(jiàn)的一類題型，其方法是多樣的，而等價(jià)代換就是眾多方法中最有效的一種。1986年，鄒兆南［2］引入了無(wú)窮大階的概念，討論了冪函數(shù)、指數(shù)函數(shù)與對(duì)數(shù)函數(shù)的無(wú)窮大的階，證明了無(wú)窮大的運(yùn)算法則和在乘除運(yùn)算中的等價(jià)替換定理，此后等價(jià)無(wú)窮大量的應(yīng)用受到眾多學(xué)者的關(guān)注，尤其是利用等價(jià)無(wú)窮大量代換求極限［3-10］，這是因?yàn)橐环矫娴葍r(jià)無(wú)窮大量代換可達(dá)到簡(jiǎn)化極限運(yùn)算的目的，但另一方面該方法也很容易導(dǎo)致出錯(cuò)。2009年，鄭婕［6］系統(tǒng)的研究了等價(jià)無(wú)窮大量在極限運(yùn)算中的四則運(yùn)算和乘方運(yùn)算的條件和結(jié)論，文中對(duì)于加法運(yùn)算的結(jié)論為:設(shè)α(x)、α1(x)、β(x)、β1(x)皆為1時(shí)的無(wú)窮大量，且1，1，若1存在且不等于1，則α(x)-β(x)～ α1(x)-β1(x)?(x→x0)。展丙軍［7］等人討論了無(wú)窮大量的比較，定義了高階無(wú)窮大量、低階大量和(A≠1)階無(wú)窮大量等概念，并舉例討論了其在級(jí)數(shù)斂散性判定中的應(yīng)用;李昌文［8］等人討論了等價(jià)無(wú)窮小量和等價(jià)無(wú)窮大量的一個(gè)誤區(qū);孫衛(wèi)衛(wèi)［1］等人闡述了等價(jià)無(wú)窮大量在(A≠1)、(A≠1)、(A≠1)、(A≠1)和(A≠1)型未定式的計(jì)算中等價(jià)代換的條件，并將文獻(xiàn)［6］中的減法運(yùn)算推廣至在某個(gè)極限過(guò)程中(A≠1)(A≠1)或?yàn)闊o(wú)窮大的情形。大量的文章研究了極限運(yùn)算中等價(jià)無(wú)窮大量的乘除運(yùn)算，而加減運(yùn)算研究的較少。本文主要研究在某個(gè)自變量的變化過(guò)程中時(shí)等價(jià)無(wú)窮大量的減法運(yùn)算，得到了該條件下無(wú)窮大量等價(jià)代換的一個(gè)充分條件，豐富和完善了無(wú)窮大量的等價(jià)代換理論。

1 預(yù)備知識(shí)

定義1［7］設(shè)函數(shù)f(x)和g(x)是在自變量的某個(gè)變化過(guò)程中的無(wú)窮大量，且也是在這個(gè)變化過(guò)程中的極限。

注2:定義2中自變量的變化過(guò)程也可以為x→-∞和x→+∞。

為了敘述的方便，已以下皆假設(shè)x→x0是大于零的常數(shù)。

2 主要結(jié)論

由定義1和定義2易得性質(zhì)1。

性質(zhì)1若在x→x0時(shí)rank［f(x)］=k，則在x→x0時(shí)x→∞是關(guān)于x→∞的同階無(wú)窮大量;若在x→∞時(shí)rank［f(x)］=k，則在x→∞時(shí)xk是關(guān)于xk的同階無(wú)窮大量。

性質(zhì)2若在自變量的同一變化過(guò)程中，rank［f1(x)］=k1＞0且 rank［f2(x)］=k2＞0，則rank［f1(x)f2(x)］=k1+k2。

證明:假設(shè) x→ x0時(shí) rank［f1(x)］=k1且 rank［f2(x)］=k2，則

rank［f1(x)f2(x)］，rank［f1(x)f2(x)］。

所以 rank［f1(x)f2(x)］，

即rank［f1(x)f2(x)］=k1+k2。在自變量的其它變化過(guò)程中的結(jié)論可類似證明。

性質(zhì)3 若在自變量的同一變化過(guò)程中，rank［f1(x)］=k1＞0且 rank［f2(x)］=+∞，則rank［f1(x)f2(x)］=+ ∞。

性質(zhì)6若f1(x)和f2(x)是在自變量的同一變化過(guò)程中的兩個(gè)無(wú)窮大量，則

證明:假設(shè)該極限過(guò)程為 x→x0.若rank［f1(x)］=+∞或rank［f2(x)］=+∞，結(jié)論顯然成立;現(xiàn)假設(shè)rank［f1(x)］=k1且 rank［f2(x)］=k2，則，則A必為常值，所以rank［f1(x)-f2(x)］≤k1.在自變量的其它變化過(guò)程中的結(jié)論可類似證明。

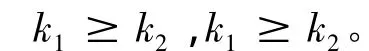
在文獻(xiàn)［1］和文獻(xiàn)［3］研究的基礎(chǔ)上，本文僅研究等價(jià)無(wú)窮大量在極限減法運(yùn)算中的如下情形。

定理2設(shè)在自變量的某個(gè)變化過(guò)程中，函數(shù) γ(x)、γ(x)、γ(x)、γ(x)、γ(x)皆是無(wú)窮大量且rank［α(x)- α1(x)］ ＜ rank［γ(x)］。若 rank［α(x)- α1(x)］ ＜ rank［γ(x)］且 rank［β(x)- β1(x)］ ＜rank［γ(x)］，則

證明:若 rank［α(x)- α1(x)］＜ rank［γ(x)］且 rank［β(x)- β1(x)］＜ rank［γ(x)］，則由性質(zhì)4 和性質(zhì)5可知，所以由定理1可知結(jié)論成立。

3 應(yīng)用舉例

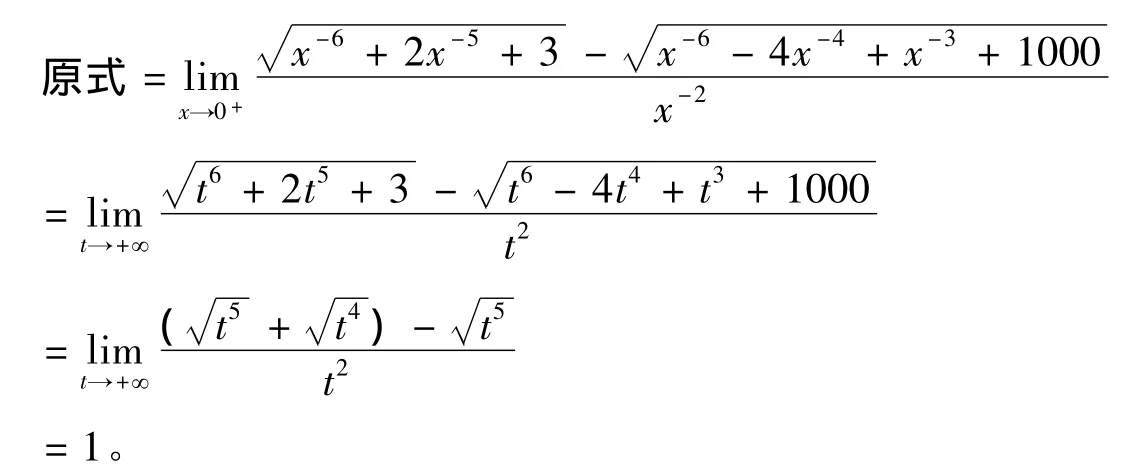
4 結(jié)語(yǔ)

本文在無(wú)窮大量階的概念的基礎(chǔ)上，得到了極限運(yùn)算中等價(jià)無(wú)窮大量加減運(yùn)算的一個(gè)新的充分條件，豐富和完善了無(wú)窮大量的等價(jià)代換理論，但是如何確定無(wú)窮大等價(jià)代換后誤差的階，還沒(méi)有特別好的辦法，值得進(jìn)一步的研究。

［1］ 孫衛(wèi)衛(wèi)，孫建英.等價(jià)無(wú)窮大在未定式計(jì)算中的應(yīng)用［J］.哈爾濱師范大學(xué)自然科學(xué)學(xué)報(bào)，2014，30(3):69-72.

［2］ 鄒兆南.無(wú)窮大的階及其運(yùn)算法則［J］.重慶交通學(xué)院學(xué)報(bào)，1986，2(17):114-120.

［3］ 甘以炎.等價(jià)無(wú)窮大及其漸近表示式［J］.葛洲壩水電工程學(xué)院學(xué)報(bào)，1996，18(4):83-85.

［4］ 常庚哲.關(guān)于無(wú)窮大量的等價(jià)［J］.高等數(shù)學(xué)研究，2000，3(3):13-15.

［5］ 王梅英，陸偉東.無(wú)窮小與無(wú)窮大的階在極限運(yùn)算及判級(jí)數(shù)斂散性中的應(yīng)用［J］.南京審計(jì)學(xué)院學(xué)報(bào)，2007，4(2):73-76.

［6］ 鄭婕.等價(jià)代換在極限求解中的應(yīng)用［J］.中國(guó)教師.高等教育，2009(1):206-207.

［7］ 展丙軍，展銘望.無(wú)窮大量的性質(zhì)及妙用［J］.大慶師范學(xué)院學(xué)報(bào)，2011，31(3):67-70.

［8］ 李昌文，潘亞麗.關(guān)于無(wú)窮小與無(wú)窮大的幾個(gè)教學(xué)誤區(qū)［J］.淮北師范大學(xué)學(xué)報(bào)(自然科學(xué)版)，2013，34(4):90-93.

［9］ 劉桂仙，劉慶升.求極限的等價(jià)無(wú)窮大代換［J］.高等數(shù)學(xué)研究，2014，1(1):51-52.

［10］ 馬志良.無(wú)窮大量與無(wú)窮大量的等價(jià)［J］.數(shù)學(xué)學(xué)習(xí)與研究，2014(7):74.