基于泰勒展開式的雙二極管模型顯示表達(dá)

楊桂紅，倫淑嫻

（1.渤海大學(xué) 數(shù)理學(xué)院，遼寧 錦州 121013；2.渤海大學(xué) 新能源學(xué)院，遼寧 錦州 121013）

目前，太陽能電池主要有兩種模型，即單二極管模型和雙二極管模型[1]。這兩種模型是關(guān)于電流電壓特性的數(shù)學(xué)描述，是隱式超越方程。為了獲得不同電壓對應(yīng)的電流值，通常采用數(shù)值方法。

然而，即使有相對好的初始猜值，這些數(shù)值方法往往難以收斂。因此，在實際的光伏發(fā)電系統(tǒng)設(shè)計與運(yùn)行的應(yīng)用中，設(shè)計工程師需要一個簡單、快速、有效的太陽能電池顯式模型。通常，太陽能電池的顯式解析表達(dá)方法根據(jù)逼近的準(zhǔn)確性可以被分為兩類。一類是以Lambert W函數(shù)為基礎(chǔ)的準(zhǔn)確的顯式表達(dá)[2]，但是Lambert W函數(shù)方法需要復(fù)雜的計算程序以及較長的計算時間；另一類是以初等函數(shù)為基礎(chǔ)的近似的顯式表達(dá)[3]。

眾所周知，雙二極管模型比單二極管模型準(zhǔn)確，尤其在低光強(qiáng)條件下[4]。因此，文中提出一個基于泰勒級數(shù)展開式的顯式雙二極管模型。而且，利用制造商提供的標(biāo)準(zhǔn)條件（SRC）下的關(guān)鍵電氣參數(shù)，建立了該顯式模型的兩個新的參數(shù)提取模型。為了驗證提出的顯式模型的有效性，本文測試了不同光強(qiáng)、溫度條件下不同材料的硅太陽能組件。

1 雙二極管太陽能電池模型

雙二極管太陽能電池等效電路由一個光生成電流源，兩個并聯(lián)二極管，一個并聯(lián)電阻和一個串聯(lián)電阻構(gòu)成。如圖1所示。

根據(jù)圖1，太陽能電池雙二極管模型的I-V特性方程可以寫成：

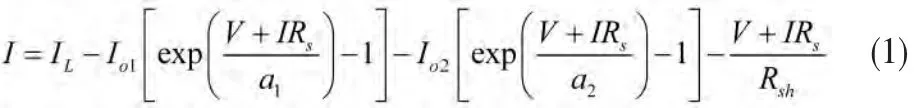
其中，I，V分別是太陽能電池的輸出電流和電壓，IL是光電流密度，Io1，Io2分別是兩個二極管反向飽和電流，Rsh是并聯(lián)電阻，Rs是串聯(lián)電阻，a1，a2分別是兩個二極管的理想因子參數(shù)。這里，，其中，n,n分別是兩個二12極管的理想因子，Ns是串聯(lián)電池的數(shù)目，q是電子電荷（1.602 176 46×10-19C），k 是玻爾茲曼常數(shù)（1.380 650 3×10-23J/K），T是電池溫度（K）。

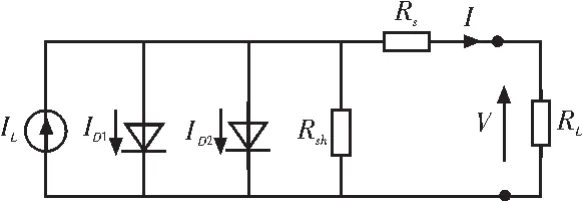
圖1 太陽能電池雙二極管電路模型圖Fig.1 The two-diode model of solar cells

2 基于泰勒展開的雙二極管模型顯式表達(dá)

式(1)中的指數(shù)函數(shù)可以采用泰勒級數(shù)近似，令x=IRs，即

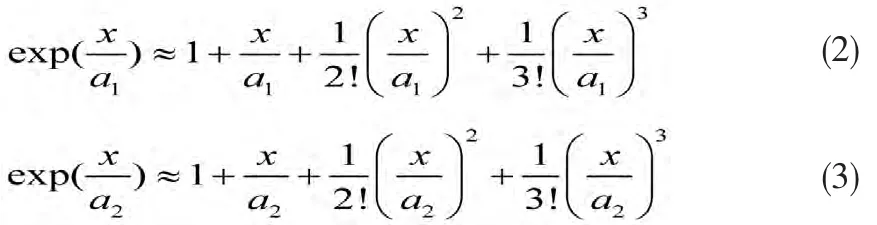
將式(2)，式(3)代入式(1)中，得到

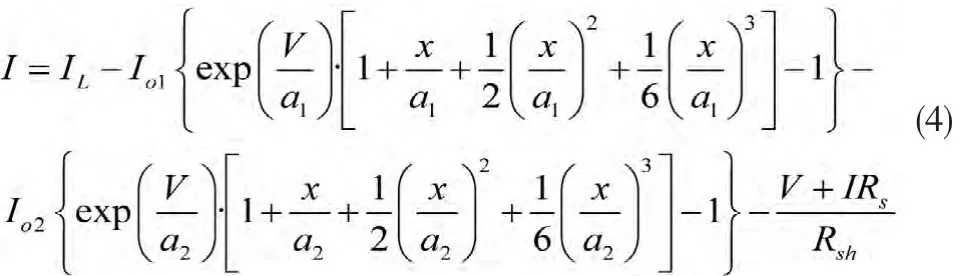
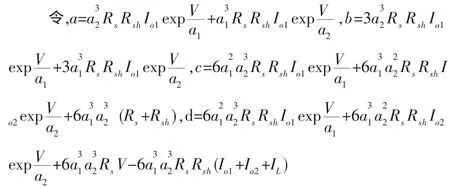
式(4)可以被重新寫成：

利用盛金公式[5]，令：

A=b2-3ac，B=bc-9ad，C=c2-3bd，根據(jù)式(1)和式(4),得到△=B2-4AC＞0，方程(5)的解為：

因此，電流I的逼近值為：

因此，式(7)是雙二極管模型的顯式解，根據(jù)式(7)可以直接計算太陽能電池的電流值。

為得到（7）中7個電池參數(shù)值，本文提出兩個基于泰勒展開式的雙二極管參數(shù)提取模型，這兩個新的參數(shù)提取模型是基本泰勒展開模型和修正泰勒展開模型。

1)基本泰勒展開模型

根據(jù)短路電流在 SRC 下的定義 V=0，I=Isc，ref，因此，式(4)可寫成：

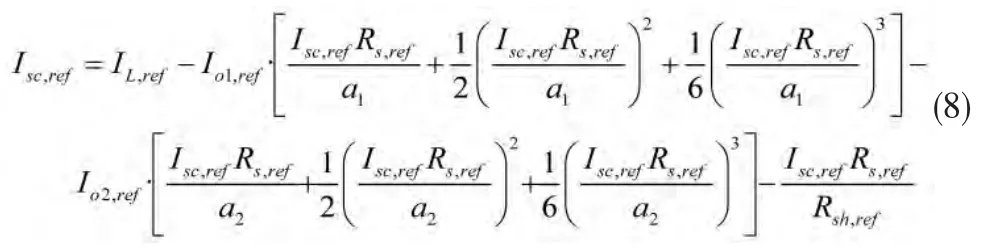
根據(jù)開路電壓在 SRC 下的定義 I=0，V=Ioc，ref，因此，式(4)可寫成：

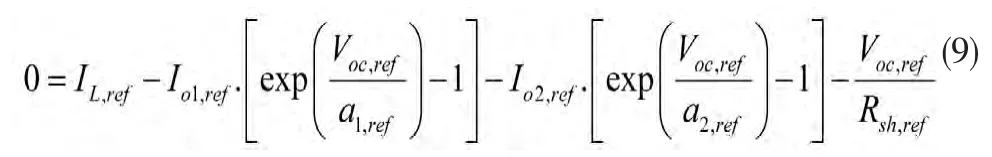
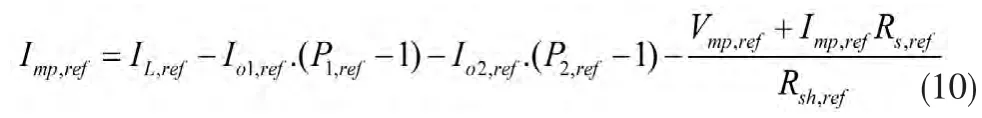
和

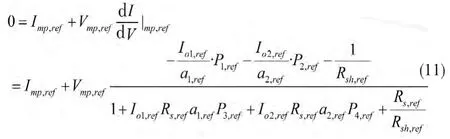
其中

由于4個方程式(8)～(11)不能求解7個未知電池參數(shù)，因此利用開路電壓溫度系數(shù)βVoc：

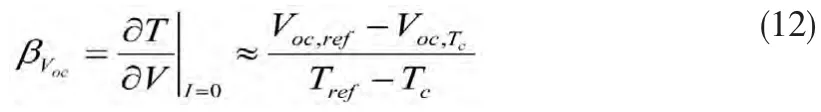
其中，Tref=298 K，Tc=Tref+10 K，βVoc，Te表示溫度為 Tc時的開路電壓溫度系數(shù)。通常βVoc由制造商提供，因此能得到βVoc，Te的值。根據(jù)式(1)和開路電壓定義，得到下面的表達(dá)式：

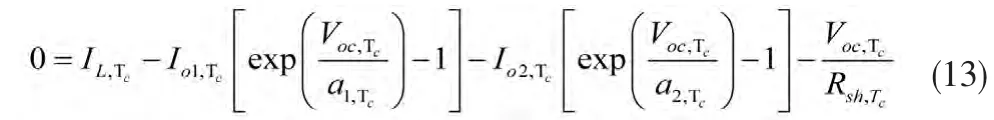
在式(13)中，需要求解，a1，Tc，a2，Tc，IL，Tc，Io1，Tc，Io2，Tc，Rsh，Tc。類似文獻(xiàn)[6]中的單二極管五參數(shù)模型，提出在不同光強(qiáng)和溫度下的，a1，a2，IL，Io1，Io2，Rsh，Rs模型：

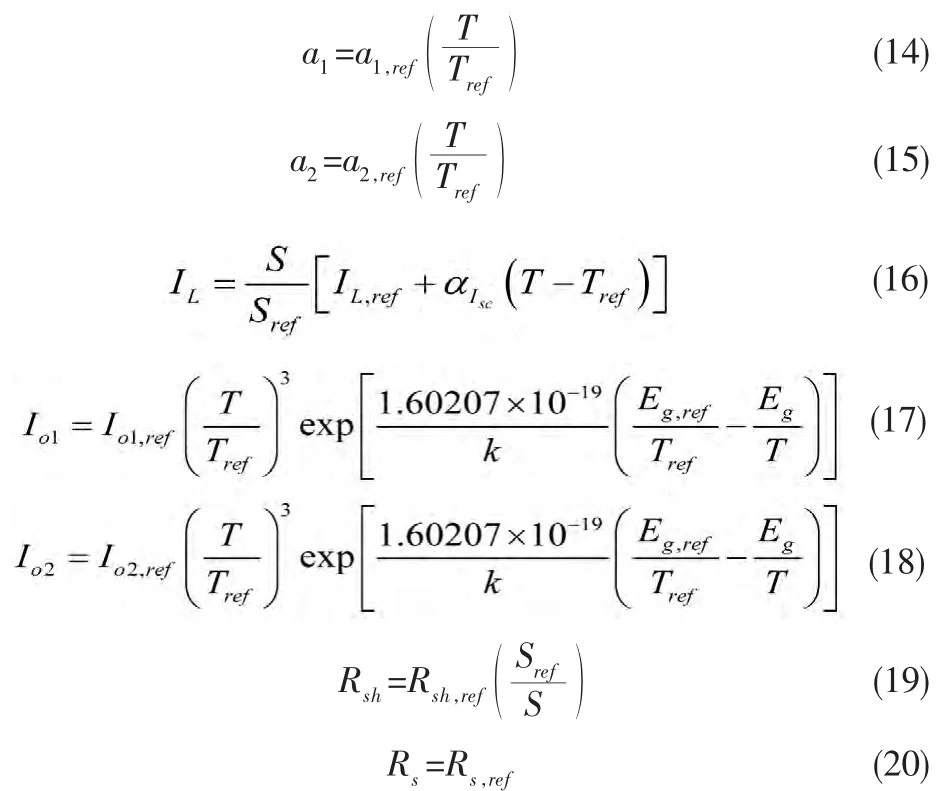
其中 Sref=1 000 W/m2，αIsc是短路電流溫度系數(shù)，Eg是材料的能帶間隙，可以表達(dá)為[6]：

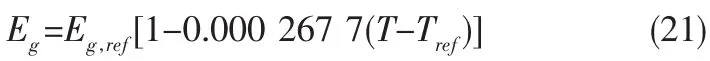
其中，對于硅電池 Eg，ref=1.121 eV。

通過增加式(13)得到5個方程求解電池參數(shù)。文獻(xiàn)[7]中提到，雙二極管模型的理想因子n1和n2滿足n1+n2≥2.2，由于本文的Ns少于72,因此，假設(shè)下面的表達(dá)式成立：

現(xiàn)在存在6個方程需求解7個未知的電池參數(shù)，因此，需要再增加一個方程。本文令I(lǐng)o2，ref=Io2，ref,guess作為已知參數(shù)值，這里Io2，ref,guess是初始猜值，表達(dá)式如下：

因此利用 6 個方程，即式（8），式（9），式（10），式（11），式（13），式（22）來獲得其他6個電池參數(shù)。綜上所述，通過使用式（14）～（21）能夠得到不同光強(qiáng)、溫度條件下的電池參數(shù)。根據(jù)式（8）～（11），去掉下角標(biāo)“ref”時，能夠得到不同光強(qiáng)、溫度條件下的 Isc，Voc，Vmp和 Imp。

上面的方法被稱為基本泰勒展開模型（BTEM），通過使用BTEM可以得到電池參數(shù)。因此，當(dāng)電池參數(shù)值代入方程（4）才真正的得到一個顯式的I-V特性模型。

2)修正泰勒展開模型

通常I-V特性曲線用來估計太陽能電池的最大功率，盡管BTEM能夠很好地表達(dá)太陽能電池的I-V特性曲線，但是在最大功率點處存在較大的模型誤差。為了減小最大功率點處的誤差，式(10)，式(11)，被修正為：

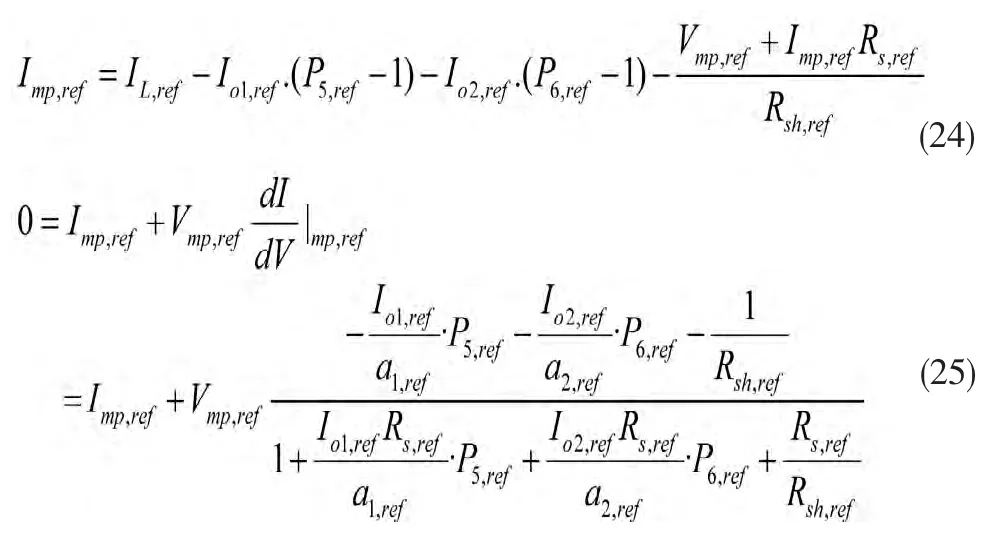
其中

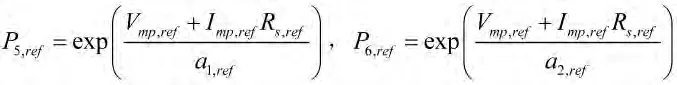
上面的方法被稱為修正泰勒展開模型（MTEM）。由BTEM到 MTEM 的轉(zhuǎn)變只是把式(10)，式(11)變成式(24)，式(25)，因此MTEM與BTEM的計算步驟相同。

3 仿真及結(jié)果分析

本文使用文獻(xiàn)[7]中的實驗數(shù)據(jù)，選擇KC200GT和SQ150PC硅太陽能組件驗證提出的模型的有效性,兩種組件在SRC下的電氣參數(shù)值由制造商提供，見表1。通過比較本文提出的BTEM和MTEM，文獻(xiàn)[7]中的雙二極管模型，文獻(xiàn)[8]中的雙二極管模型，文獻(xiàn)[3]中的單二極管模型，驗證本文提出的兩個模型的準(zhǔn)確性。定義均方根誤差（RMSE）為：

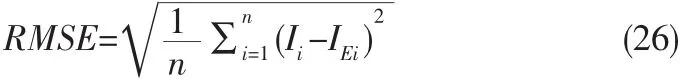
其中Ii是測試模型的電流，IEi是測量數(shù)據(jù)的電流，n是測量數(shù)據(jù)的個數(shù)。本文測試KC200GT組件的I-V特性見圖2和圖3。測試SQ150PC組件的I-V特性見圖4和圖5。另外，分別計算KC200GT組件和SQ150PC組件的RMSEs，見表2。在SRC下，文中提出的BTEM，MTEM和文獻(xiàn)[3]中模型計算不同組件的電池參數(shù)值,見表3。

表1 標(biāo)準(zhǔn)條件下由制造商數(shù)據(jù)提供太陽能組件電氣參數(shù)值Tab.1 Electrical characteristics of solar modules by manufacturer's datasheet at SRC

由圖2至圖5，通過計算絕對誤差可知，BTEM，MTEM，文獻(xiàn)[7]模型和文獻(xiàn)[3]模型的KC200GT組件的最大絕對誤差在光強(qiáng)S=1 000 W/m2，溫度T=25℃時分別為0.657 5，0.533 4，0.665 8，0.533 4，文獻(xiàn)[8]模型的 KC200GT 組件的最大絕對誤差在光強(qiáng)S=1 000 W/m2，溫度T=75℃時為1.342 3。以上5個模型的SQ150PC組件的最大絕對誤差在光強(qiáng)S=1 000 W/m2，溫度 T=60 ℃時分 別為 0.527 0，0.456 2，0.515 3，0.456 4，0.485 1。另外，從表3可以看出MTEM的RMSEs比其他4個模型相對小些。因此，本文提出的兩個模型比其他模型更能夠準(zhǔn)確地逼近I-V特性。

4 結(jié)論

本文基于泰勒展開模型獲得新的太陽能電池雙二極管模

型的顯式解析表達(dá)[9]。本文呈現(xiàn)的模型能夠根據(jù)制造商提供的數(shù)據(jù)直接計算不同電壓的電流值。因此，在實際的光伏發(fā)電系統(tǒng)設(shè)計與運(yùn)行的應(yīng)用中，本文提出的模型能夠通過直接使用制造商數(shù)據(jù)快速、準(zhǔn)確地估計太陽能組件性能。

表2 不同模型的均方根誤差Tab.2 RMSEs of the different models for PV modules

表3 根據(jù)制造商數(shù)據(jù)獲得的不同模型電池參數(shù)值Tab.3 Cell parameter values of different models obtained by using manufacturer's datasheet

圖2 KC200GT溫度為25℃時I-V圖Fig.2 I-V for KC200GT at T=25℃

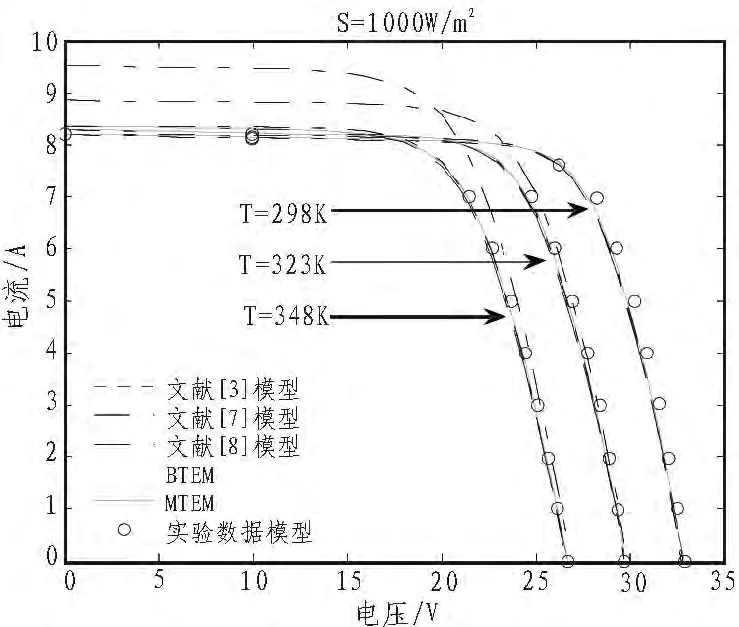
圖3 KC200GT光強(qiáng)為1000W/㎡時I-V圖Fig.3 I-V for KC200GT at S=1000W/㎡

圖4 SQ150PC溫度為25℃時I-V圖Fig.4 I-V for SQ150PC at T=25℃

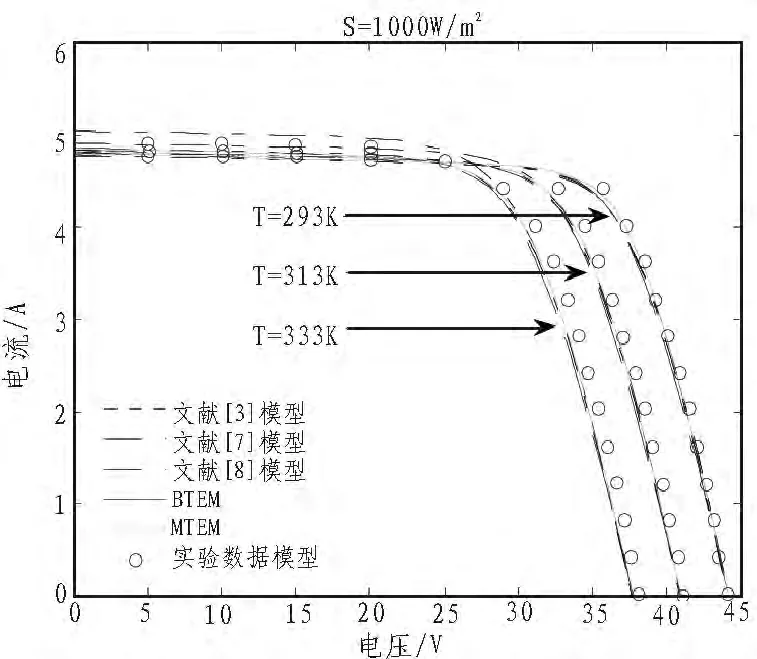
圖5 SQ150PC光強(qiáng)為1000W/㎡時I-V圖Fig.5 I-V for SQ150PC at S=1000W/㎡

[1]Cheknane A,Hilal H S,Djeffal F,et al.An equivalent circuit approach to organic solar cell modeling[J].Microelectronics Journal,2008(39):1173-1180.

[2]Romero B,Del POZO G,ARREDONDO B.Exact analytical solution of a two diode circuit model for organic solar cells showing S-shape using Lambert W-functions[J].Solar Energy,2012(86):3026-3029.

[3]LUN Shu-xian,DU Cun-jiao,GUO Ting-ting,et al.A new explicit I-V model of a solar cell based on Taylor's series expansion[J].Solar Energy,2013(94):221-232.

[4]Kurobe K,Matsunami H.New two-diode model for detailed analysis of multicrystalline silicon solar cells[J].Applied Physics,2005(44):8314-8321.

[5]范盛金.一元三次方程的新求根公式與新判別法[J].海南師范學(xué)院學(xué)報,1989(2):91-98.

[6]DE SOTO W,Klein S A,Beckman W A.Improvement and validation of a model for photovoltaic array performance[J].Solar Energy,2006,80(1):78-88.

[7]Ishaque K,Salam Z,Taheri H.Simple,fast and accurate two diode model for photovoltaic modules[J].Solar Energy Materials,2011(95):586-594.

[8]Hejri M,Mokhtari H,Azizian M R,et al.On the parameter extraction of a five-parameter double-diode model of photovoltaic cells and modules[J].IEEE Journal of Photovoltaics,2014(4):915-923.

[9]張相華，彭國良，杜太焦，等.一種通用的含熱阻溫度場計算方法[J].現(xiàn)代應(yīng)用物理，2015（1）：60-65.