常州地區土的塑性指數與滲透系數的經驗關系研究

孫 君 ，丁云飛

（常州市規劃設計院，江蘇常州 213000）

0 前言

常州地區位于長江三角洲蘇南太湖平原西北部，區內地面下深度0～70m普遍分布多層粘性土、粉土，其滲透系數作為一項重要的參數指標，對土體強度、變形都具有重要影響[1]，建立滲透系數與土工試驗參數間的經驗關系也是工程實踐中值得關注的問題[2-4]。

粘性土、粉土的滲透系數與顆粒級配、礦物成分、結合水膜的厚度、結構構造等多因素關系緊密[5]，這些影響因素從土工試驗各參數中得到不同程度的體現，其中塑性指數IP與滲透系數K關系更為密切。

通過對常州地區粘性土、粉土塑性指數與滲透系數多組數據的綜合分析，筆者認為其塑性指數與滲透系數存在明顯的相關性，并初步建立了兩者的經驗關系。對該區域粘性土、粉土滲透系數的快速確定具有實際意義。

1 試驗指標

數據來源：研究數據共157組，數據范圍塑性指數IP5.2～19.3；滲透系數K 3.3×10-8cm/s～2.5×10-4cm/s,主要來源于軌道交通詳勘，數據可靠性高，分布區域廣，代表性好。

試驗方法[6]：塑性指數IP，其液限采用錐式法10mm液限、塑限采用搓條法；滲透系數K，采用變水頭滲透試驗。

2 相關關系分析

2.1 回歸方程建立

在直角坐標系中，以塑性指數IP為橫坐標，滲透系數的自然對數ln(K)為縱坐標，建立散點圖進行分析，不難發現IP與ln(K)之間存在線性關系，滲透系數K與IP呈反比，如圖1所示。

圖1 IP與ln(K)經驗關系散點圖

由此建立兩者之間關系：l n(K)=а+β(IP)，設y=ln(K)，x=IP，即y= а+βx,最小二乘法系數а、β和相關系數r計算如式(1)～式(3)：

2.2 回歸方程計算

根據最小二乘法回歸分析原理[7]，關鍵步驟為式(1)、式(2)、式(3)計算а、β、r，涉及的計算項如表1所示：

將表1中數據代入式(1)、式(2)，得：

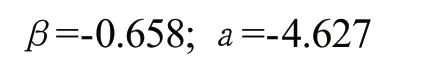
因此，回歸方程為：ln(K)=-0.658-4.627IP

將表1中數據代入式(3)，求得相關系數：

r=-0.988

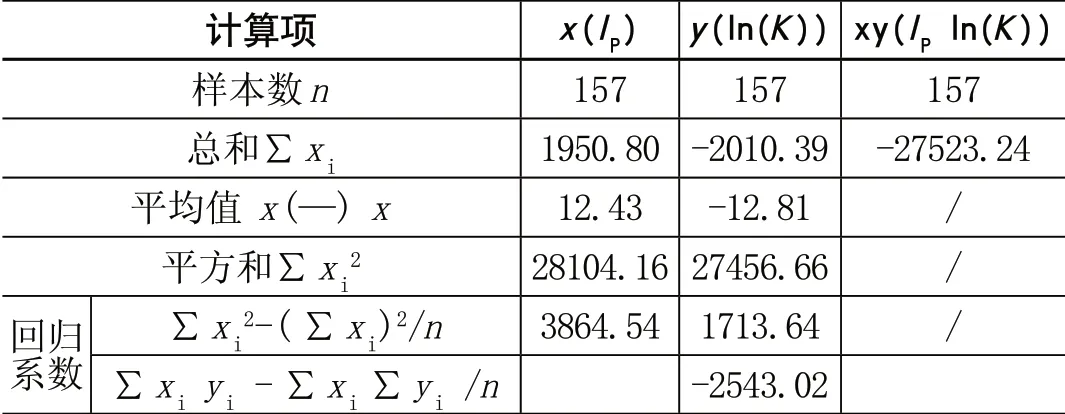
表1 回歸分析計算過程表

2.3 回歸方程顯著性

利用方差分析法進行檢驗回歸方程的顯著性，如表2所示：

(1)總平方和Lyy及自由度fyy Lyy=∑yi2-(∑yi)2/n=1713.64 fyy=n-1=157-1=156

(2)回歸平方和U及自由度fU U=β(∑xi yi-∑xi∑yi /n)=1673.31 fU=1

(3)剩余平方和Q及自由度fQ Q= Lyy-U=1713.64-1673.31=40.33 FQ= n-2=157-2=155

根據方差分析法可知，回歸方程顯著性評價結果為高度顯著，即表明塑性指數Ip與滲透系數自然對數ln(K)間的經驗關系高度顯著。

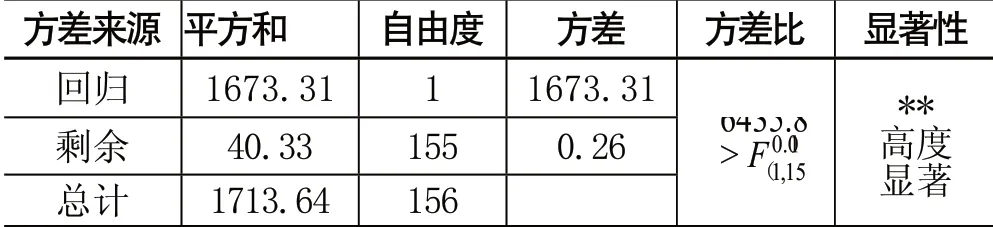
表2 顯著性分析表

3 地區經驗關系表

本文研究數據塑性指數范圍Ip5.2～19.3，根據回歸方程式(4)，建立常州地區塑性指數Ip與滲透系數的經驗關系，如表3所示：

由表3可知，粘性土、粉土的滲透系數隨著塑性指數的增大而較小，土類與滲透系數的經驗關系為：

粉土：K≥1.36×10-5cm/s

粉質粘土：K=1.36×10-7～1.36×10-5cm/s

粘土：K≤1.36×10-7cm/s

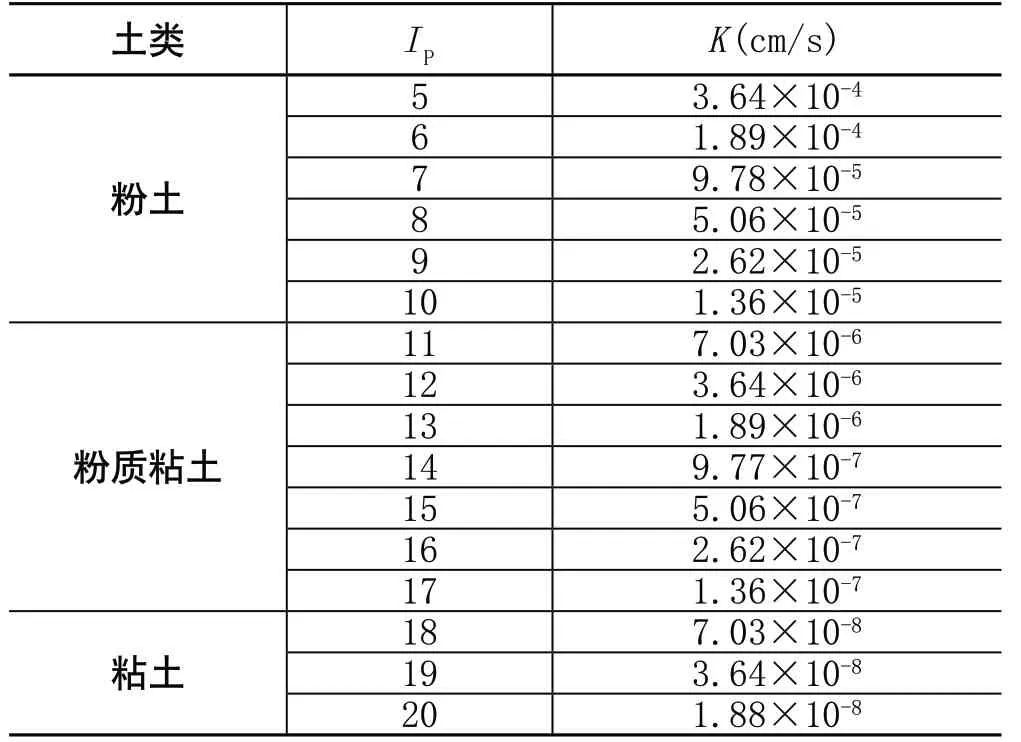
表3 IP與K經驗關系對照表

4 結語

通過對常州地區粘性土、粉土(IP5.2～19.3)塑性指數與滲透系數的數據分析，建立了塑性指數IP與滲透系數自然對數ln(K)的線性相關關系，并推導得到常州地區塑性指數Ip與滲透系數K的經驗關系式。

顯著性檢驗結果表明塑性指數IP與滲透系數K經驗關系高度相關。由此建立的塑性指數IP與滲透系數K經驗關系對照表，對本地區滲透系數的快速確定，具有借鑒價值。

[1]孔令偉，李新明，田湖南.砂土滲透系數的細粒效應與其狀態參數關聯性[J].巖土力學，2011，32(S2)：21～25.

[2]鄧永鋒，劉松玉，章定文等.幾種孔隙比與滲透系數關系的對比[J].西北地震學報，2011，33(S1)：64～66.

[3]張 真.由固結試驗成果推算弱透水性土的滲透系數[J].桂林工學院學報，1996，16(1)：73～77.

[4]呂衛清，董志良，陳平山等.正常固結軟土滲透系數與固結應力關系研究[J].巖土力學，2009，30(3)：769～773.

[5]張克恭，劉松玉.土力學[M].北京：中國建筑工業出版社，2001.

[6]王靜龍.應用線性回歸[M].北京：中國統計出版社，1998.