角接觸球軸承載荷的自動分析系統

韓澤光，李墩強，郝瑞琴，郝 婷，張 磊，程晶晶

（沈陽建筑大學 機械工程學院，遼寧 沈陽 110168）

0 引言

角接觸球軸承的載荷是決定其能否正常運行和合理設計的關鍵設計參數。在實際工作中，角接觸球軸承所受載荷隨著所用結構的設計不同而變化，載荷的大小與軸的支撐數量、安裝方式、外載荷類型、大小、方向、數量和載荷作用點位置等密切相關，其計算方法比較復雜，容易出錯，因此對角接觸球軸承的受載分析方法引起國內外研究人員的廣泛重視，取得了一些卓有成效的研究成果。代表性的有：Harris[1]對角接觸球軸承受外力作用下的靜載荷進行了詳細研究，介紹了球軸承在軸向力、徑向力和力矩聯合作用下的載荷分析方法。程超等[2]利用NEton-raohson 法進行了雙列角接觸球軸承載荷分布計算。Choi[3]等則在忽略力矩的前提條件下，分析了雙列角接觸球軸承的承載情況。唐云冰等[4]建立了滾動軸承的載荷分布的有限元模型，分析了載荷參數對軸承接觸應力、接觸角和變形的影響規律。李慧云、高仲達、張永貴、謝昭童[5]等利用支承在載荷作用下的變形呈線性關系，對三支承結構的機床主軸剛度公式進行了推導。Yu[6]等分析了軸承在聯合載荷作用下的承載情況，并利用NAGA-II 算法對軸承結構進行了優化。上述研究針對作用在軸承上的載荷已知的情況，沒有考慮軸系中傳動零件外載荷與角接觸球軸承內部軸向力聯合作用情況，以及三支承超靜定類軸系軸承的受載問題，且沒有形成常用軸系的軸承載荷通用計算方法，尚未實現該類軸承設計的自動化，導致設計效率低下。基于此，我們推導了角接觸球軸承載荷的通用計算方法，研制了簡單實用的自動計算系統，使設計人員僅需進行少數基本設計參數的交互即可迅速獲得角接觸球軸承載荷值，大大提高了設計效率，保證了計算的正確性，為該類軸承的進一步研究奠定了基礎。

1 角接觸球軸承載荷計算理論

在實際軸系中，軸承所在軸的支承方式大多采用雙支承和三支承的形式，同一支點處還會出現成對安裝同種型號的角接觸球軸承形式。當軸上安裝多個齒輪、帶輪、鏈輪等不同傳動零件時，軸承的載荷計算比較復雜，需要分類分析并導出其計算通式。

1.1 角接觸球軸承徑向載荷計算

（1）兩軸承簡支布置。圖1（a）為兩軸承簡支布置力學模型，假設從左至右的四個作用點（序號依次是4、1、2、3）位置均裝有傳動零件，該模型可以表達實際軸系中兩傳動零件簡支布置、兩傳動零件一個簡支一個懸臂、傳動零件在軸承左或右側布置、以及存在兩個以上傳動零件的情況，依據該模型可以導出軸承的徑向載荷計算通式。假設圖1（a）中每個作用點受到三個分力Fti、Fai、Fri作用，作用點位置用mi、ri來表示，下標i 表示作用點序號，其值為1、2、3、4。根據支承點的力矩和力的平衡方程可得左、右兩側軸承所受徑向載荷FrI和FrII的表達式：

圖1 力學模型Fig.1 Mechanical model

（2）三軸承支承布置。在立式高速銑削主軸等的設計中普遍采用三軸承支承形式，此時軸承受力為超靜定問題，為了確定軸承的載荷，力學模型可簡化為圖1（b）的形式，并假設：①各支承處軸承的力矩和為0；②各軸承的徑向位置變動忽略不計；③軸的截面慣性矩相同。傳動零件數量、載荷和作用位置如圖4 所示，每個作用點處的三個分力用Fai、Fti、Fri（i=1、2、3、4）表示，根據M1=M2=M3，δ1＝δ2，J1=J2（J 是指軸的截面慣性矩，δ 是指軸的位置變動），I 軸承的徑向載荷為：

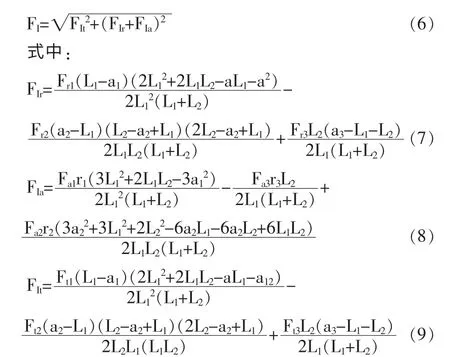
限于篇幅，略去其余兩支承的的力學公式。

（3）同一支點成對安裝同種型號角接觸球軸承的徑向載荷計算。在角接觸球軸承的實際使用中，為了保證主軸的穩定性，常常需要在同一個支點成對安裝同一型號的角接觸軸承。此時將成對軸承看作是雙列軸承，反力的作用點位于兩軸承的中點處，因此同一支點上兩個軸承的所受徑向力Fr1、Fr2與支點處的合力Fr之間滿足：

1.2 角接觸軸承軸向載荷計算

（1）兩軸承簡支布置。兩角接觸球軸承簡支布置的安裝方式分為正裝和反裝，以圖2（a）的正裝安裝方式為例介紹軸承的軸向載荷計算方法。設軸承的判斷系數為e（對應軸承接觸角15°、25°、40°的值分別為0.4、0.68、1.14），則：①若Fr1e ＞eFr2+Fa，軸承1 處于放松狀態，軸承2 處于壓緊狀態，則Fa1=Fr1e，Fa2=Fr1e－Fa；②若Fr1e＜eFr2+Fa，軸承1 處于壓緊狀態，軸承2 處于放松狀態，則Fa1=Fr1e+Fa，Fa2=Fr1e；③若Fr1e=eFr2+Fa，兩個軸承都處于放松狀態，則Fa1=eFr1，Fa2=eFr2。

反裝時軸承的軸向載荷的計算方法具體見文獻[7]。

（2）同一支點成對安裝同種型號角接觸球軸承的軸向載荷計算。在圖2（b）中，同一個支點成對安裝同一型號的角接觸軸承（正裝或反裝），其軸向載荷計算方法如下：以反裝方式為例，力學模型如圖2（b），結合上述的同一支點處兩軸承的徑向載荷為Fr1=Fr2=0.5Fr，則：①若Fa＞0，軸承1 處于放松狀態，軸承2 處于壓緊狀態，則Fa2=Fre+Fn，Fa1=Fre；②若Fa＜0，軸承1 處于壓緊狀態，軸承2 處于放松狀態，則Fa1=Fre-Fa，Fa2=Fre；③若Fa=0，兩個軸承都處于放松狀態，則Fa1=Fa2=Fre。

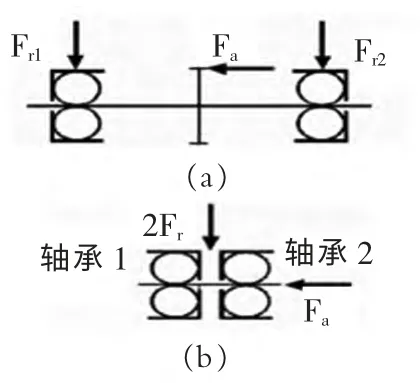
圖2 軸承安裝方式Fig.2 Installation type of bearing

2 角接觸球軸承載荷計算自動化系統的實現

為方便完成角接觸球軸承的載荷計算，應用Visual Basic6.0 軟件設計了角接觸球軸承載荷計算自動化系統，系統的主界面如圖3（a）和（b）所示。整個系統界面是由三部分組成，本文僅介紹載荷計算的部分，點擊圖3（a）的載荷計算控件，彈出圖3（b）載荷計算界面，選擇支承類型，彈出對應的支承方式界面，如圖3（c）和（d）所示，在對應界面中輸入相關參數，即可完成角接觸球軸承的載荷計算。

圖3 系統界面Fig.3 System interface

3 實例

圖4 軸的力學模型Fig.4 Mechanical model of shaft

某減速器傳動軸的力學模型如圖4 所示，軸左側裝直齒輪，兩支承中間裝有斜齒輪，其L=130mm、L1=40mm、L2=70mm，直齒輪的直徑為D1=45.58mm，斜齒輪直徑為D2=186.42mm，Fr1=350N、Ft1=927N、Fr2=842N、Ft2=2235N、Fa2=274N，求軸承所受的載荷。

應用本軟件系統，在圖3（c）和（e）中輸入相應的參數值，當軸承型號選擇70000AC（e=0.68）、反裝、異點支承的方式時,兩支承處的徑向載荷分別為4249.91N、885.93，軸向載荷分別為 2289.9388N、3163.9388N，（見圖5(a)）。當選用70000B（e=1.14）且采用同一支點兩個軸承正裝的方式時（圖5（b）），成對安裝兩軸承的徑向載荷都為2124.95N，軸向載荷分別為2696.443N、2422.443N。

圖5 軸承的受力Fig.5 Force of bearing

4 結論

（1）建立了角接觸軸承受載的通用化模型，推導了不同形式下軸承載荷計算的通式。

（2）研制了角接觸軸承載荷計算的自動系統，實現了徑向載荷、軸向載荷的實時計算，方便設計人員快速獲得角接觸球軸承的載荷大小，為角接觸球軸承的進一步設計提供了依據。

（3）系統集分類、設計、計算于一體，界面友好，使用快捷、方便，可有效支撐設計人員的軸承研究工作。

[1]Harris T A．Rolling bearing analysis [M]． New York:John Wiley ＆Sons，2001.

[2]程超，汪久根.雙列角接觸球軸承的載荷分析[J].機械科學與技術，2014，6.

[3]Choi D H，Yoon K C． A design method of an automotivewheelbearing unit with discrete design variables usinggenetic algorithms[J]． Journal of Tribology，2001，123.

[4]唐云冰，高德平，羅貴火.航空發動機滾動軸承的載荷分布研究[J].航空學報，2006，6.

[5]李慧云，高仲達，張永貴，等.機床三支承主軸剛度的計算[J].機床與液壓，2010，23.

[6]Yu W，Ren C Z． Optimal design of high speed angularcontact ball bearing using a multi-objective evolutionalgorithm ［C］//2010 International Conference onComputing，Control and Industrial Engineering，Piscataway: IEEE Computer Society，2010.

[7]韓澤光，鄭夕健，等.機械設計[M].北京航空航天大學出版社，2011.