基于GPS軌跡的周期模式發現
李海
(江蘇科技大學 計算機科學與工程學院,江蘇 鎮江 211003)
智能手機和穿戴設備的興起使得GPS軌跡記錄的采集越來越方便,也為軌跡數據挖掘研究帶來了極大的便利。由于人類活動是有著某些顯著的且相對固定的移動模式[1],所以周期模式的挖掘不僅為移動數據的壓縮提供了幫助[2-3]同時還可以用來預測該對象未來的移動方向[4]及發現移動對象的異常行為。然而,從GPS記錄中發現用戶的周期模式是一件非常有挑戰的事情。其中有兩個主要問題需要解決:如何有效預處理GPS數據和如何從時間序列的發現周期模式。
已經有很多人針對周期模式發現這個問題進行了研究,但是他們很少考慮到GPS數據特殊性:數據不是完全正確、采樣頻率的不確定、數據的不完整等。2010年,Li提出將傅里葉變換和自相關系數結合尋找周期模式[5],該方法的不足之處在于采樣頻率過低和數據不完整的情況下,很少能找到周期模式。由于用戶的GPS設備不一定是隨時都處于工作狀態以及面臨大量用戶數據的時候,采樣點過密,會產生大量的數據冗余,所以文中主要研究如何處理低采樣的情況。
針對GPS數據的特殊性,文中提出一種周期模式的發現方法GMPF(GPSMulti-Periodic Find),可以有效處理數據稀疏和不完整的問題。基本的算法思路:首先對GPS記錄進行預處理并聚類得到需要的興趣點,然后對興趣點進行采樣得到多個二進制的序列,最后采用基于概率的周期發現算法,從二值序列中發現每個興趣點的周期模式。
1 GMPF算法框架
GPS記錄是由一系列 GPS點構成的[6],表示為 P={p1,p2,…,pn},每個GPS點數據由經度,緯度和時間戳構成,pi∈P且pi=(Lat,Lngt,t)。
定義1(GPS軌跡):GPS軌跡可以看成是關于GPS點的時間序列。Tra={p0,p1,…,pn},?0≤i≤n,pi+1·t>pi·t,其中pi(0≤i≤n)是 GPS 采樣點。
定義 2(停留點):一個停留點表示一個區域范圍(θd表示區域半徑)用戶停留的時間超過了設定的時間閾值θt。停留點就是符合以下定義的GPS點的集合P=
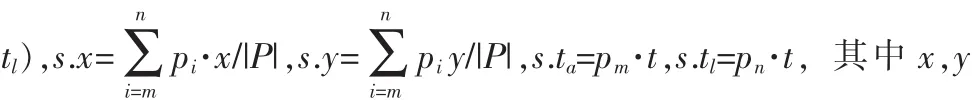
表示當前停留點的中心坐標,代表這個停留點的位置,ta表示停留點起始時間點,tl表示停留點的結束的時間點。
定義3(行為的周期模式):一個行為的周期模式可以表示成
從上面的定義,文中提出一個兩步驟的周期發現算法GMPF(GPSMulti-Periodic Find)。
算法1:GMPF(多周期模式發現)
輸入:一個GPS移動序列LOC=loc1loc2…locn
輸出:一系列興趣點的周期模式
1:/*階段1:檢測GPS中興趣點*/
2:Find stay spots S={s1,s2,…,sn}; //找到所有的停留點
3:O=ClusterStayPoint(S);//通過聚類停留點,得到興趣點
4:/*階段2:檢測每個興趣點的周期模式*/
5:for each oi∈O do
6:P=MinePeriodPattern (oi);//對每個興趣點進行周期模式挖掘
7:constructPeriodPatternOutput (P);//構造周期模式輸出結果
算法1描述了GMPF的基本的框架。在第一個階段主要是找到所有的興趣點(2-3行),然后對每一個興趣點進行周期模式挖掘并輸出相應的結果(5-7行)。
2 興趣點發現
本文主要是處理兩類停留點,第一類停留點就是一個人進入了某個區域,然后在這個區域徘徊的時間超過了一個閾值;第二類情形就是一個人GPS記錄保持停止狀態的時長超過了某個閾值。
興趣點發現是對上一步得到的停留點集合進行聚類分析,得到其中被訪問次數較高的區域。文中提出一個依賴于閾值假定的聚類方法,其思想類似于DBSCAN,但是不需求去計算鄰域,而是去掃描已經存在簇,當數據的密度比較高的時候,效率會遠高于DBSCAN,在最壞的情況下也要比DBSCAN的時間復雜度要小。由于本文主要挖掘GPS序列中的周期模式,一般來說存在大量周期模式的數據中必然存在大量的高密度數據簇。
首先從停留點集合中抽出一個未處理的點,然后遍歷當前所有的簇的集合,檢測該點是否屬于某個簇,如果存在這樣的簇的話,則更新簇的中心。否則認為這個點是一個新的簇。最后檢測每個簇的計數是否滿足最小計數的要求。
3 周期模式挖掘
3.1 移動序列二值化
現在得到了一系列的興趣點,下面主要是針對每一個興趣點進行挖掘,找出其中潛在的周期模式。以其中的一個興趣點為例,首先對整個移動序列進行采樣,將這個移動序列轉換成一個二進制序列 B=b1,b2,…,bn,當這個移動對象在時間點i的時候在這個興趣點區域內,則bi=1,否則 bi=0。
3.2 二進制序列周期挖掘模型
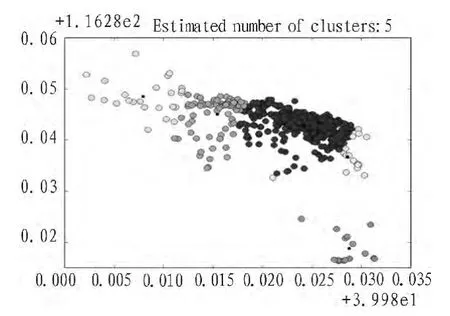
定義4(周期序列)在一個序列X=x(t),0 定義 5 (周期分布向量)定義向量 p=[p0,p1,…,pT-1]∈[0,1]是一個長度為 T的周期分布向量,x(t)是獨立且服從pmod(t,T)伯努利分布,則 X=x(t)就是一個服從周期向量分布 p的二值序列。 定義 6:假設 X 是一個二值序列,定義 S+={t:x(t)=1},S-={t:x(t)=0}。 It表示[0:T-1]的冪集,其中 T 表示一個候選周期。對于任何?I∈It,定義 S+I={t∈S+:FT(t)∈I},S-I={t∈S-:FT(t)∈I},其中 FT(t)=mod(t,T),進一步用比率形式表示 μx+(I,T)= 定理1:對于一個長度為n且服從周期向量分布P的二 現在介紹基于定理1的周期發現方法,對于任意的I∈IT,Δx(I,T)=μx+(I,T)-μx-(I,T)。 當 T 是本序列的周期,則滿足下面的條件 γ(T)=Δ(I,T),顯然 0≤γx(T)≤1。 當序列 X完全符合以T為周期的時間序列,則γ(T)=1。但是這些只能說明在什么情況下的T是符合要求的,下面還要介紹如何才能找到這個周期T。 可以得到: 經過3.1節的移動序列二值化以后,就可以把得到序列看成是一個服從某個周期向量分布的序列。在3.2節中已經介紹了文中尋找潛在周期T的方法,就是計算每一個周期T的可能性,然后取概率最大的一個,具體的步驟如下: 1)設定一個最大周期Tmax 2)從區間[1,Tmax]中按序取出一個值,賦值給T0 3)用公式(1)和(2)計算T0是目標序列周期的概率 4)重復第二步,直到完全遍歷 5)取計算得到的最大P對應的T0,這就是當前序列的周期 假設一個最大可能的周期Tmax,然后通過公式計遍歷計算[1,Tmax],取P最大的那個T,作為本條序列的周期。 本實驗的運行環境是 Windows 7操作系統,算法的編寫使用 Python語言。主要開發軟件環境包括:1)Spyder作為實驗算法實現和性能測試程序的開發環境;2)MySQL作為數據庫存儲平臺。本文使用的數據集是微軟亞洲研究院Geolife項目所采集到的數據。 算法驗證1:為了驗證文中的對興趣點的聚類算法的有效性,本文在geolife的編號為0的用戶的數據集上進行了實驗,同時將實驗的結果同Yu文章中使用的聚類方法DBSCAN得到的結果進行比較。 GPS記錄點總數是173 870,通過停留點分析,得到 823個停留點。然后通過對停留點分別使用DBSCAN和本文的興趣點聚類算法進行聚類。實驗結果如圖1和圖2所示。 圖1 DBSCAN聚類結果Fig.1 Result of DBSCAN cluster 圖2本文方法聚類結果Fig.2 Result of our cluster method 由于DBSCAN密度可達是直接密度可達的傳遞閉包,并且這種關系是非對稱的,使其對數據集的密度極為敏感。如圖1所示,數據被聚類成2個簇,其中簇1中包含了764個點,簇2中包含了23個點。如圖2所示,文中提出的算法將數據劃分成了5個簇,所包含點的個數分別為110,294,118,15,17,50。結合本GPS數據的特點,人們日常生活的移動軌跡數據,可以看出本文的算法更符合現實特點。 算法驗證2:二值化序列的周期挖掘算法驗證比較,為了驗證本文周期挖掘算法在低采樣情況下的有效性,將文獻中[5]提出的FFT集合自相關系數,以及文獻[7]中提出的幾種二進制序列周期發現方法和本文的周期挖掘算法進行比較。圖3,4,5分別是本文的方法自相關系數結合傅里葉算法、傅里葉結合直方圖算法在不同采樣率情況下的實驗結果。 由圖3~5所示,可以發現在高采樣的情況下,3種算法都是表現良好,但是當降低采樣頻率后,后3種方法就不能得到正確的周期了。由此可以看出本文提出的周期算法對低采樣的情況有較好的表現。 實驗驗證3:在geolife的編號為0的用戶的數據集上,綜合驗證本文的算法。在實驗1中得到了5個興趣點,由于后兩個興趣點的密度較小,所以只選用前3個興趣點進行驗證,假設這三興趣點分別是公司、家、健身館。最后的得到的實驗結果如表1。 圖3本文方法Fig.3 Our method 從表中可以看出該用戶的周期模式分別是一天和一周為單位的,符合日常的行為習慣。 圖4自相關系數結合傅里葉算法Fig.4 Autocorrelation coefficient combined with Fourier algorithm 圖5傅里葉結合直方圖算法Fig.5 Fourier combined histogram algorithm 表1 用戶的周期模式檢測結果Tab.1 Result of Person periodic pattern 本文針對移動對象的周期性問題,提出了一個GMPF算法,主要有兩個部分構成。第一個部分找到興趣點,不同的興趣點在時間上是可以重疊的,這個也就解決了同時存在多個周期模式的問題。第二部分主要是挖掘周期模式,由于GPS[8]數據采樣頻率的不確定性,采用基于概率統計的方法來尋找周期。實驗結果表明本文的方法在數據非常稀疏的情況下,也可以取得較好的表現。本文提出的算法框架在最壞情況下的時間復雜度是O(n*n),這個還可以進一步的改進與提高,也是將來研究的一個方向。 [1]Gonzalez MC,Hidalgo C A,Barabasi A L.Understanding individualhumanmobilitypatterns[J].Nature,2008,453(7196):779-782. [2]Cao H,Mamoulis N,Cheung D W.Discovery of periodic patterns in spatiotemporal sequences[J].IEEE Transactions on Knowledge and Data Engineering,2007,19(4):453-467. [3]Xia Y,Tu Y,Atallah M,et al.Reducing Data Redundancy in Location-Based Services[C]//Geosensor,2006.InProcs.of 2nd International Conference on Geosensor Networks,2006:30-35. [4]Jeung H,Liu Q,Shen H T,et al.A hybrid prediction model for moving objects[C]//IEEE 24th International Conference on.IEEE,2008:70-79. [5]Li Z,Ding B,Han J,et al.Mining periodic behaviors for moving objects[C]//Proceedings of the 16th ACMSIGKDD international conference on Knowledge discovery and data mining.ACM,2010:1099-1108. [6]Zheng Y,Zhang L,Xie X,et al.Mining interesting locations and travel sequences from GPS trajectories[C]//Proceedings of the 18th international conference on World wide web.ACM,2009:791-800. [7]Junier I,Hérisson J,Képès F.Periodic pattern detection in sparse booleansequences[J].Algorithms for Molecular Biology,2010(5):31. [8]雷娟,劉文霞.GPS數據采集分析器設計 [J].電子科技,2013(5):30-33.LEI Juan,LIU Wenxia.Design of a GPS data acquisition analyzer[J].Electronic Science and Technology,2013(5):30-33.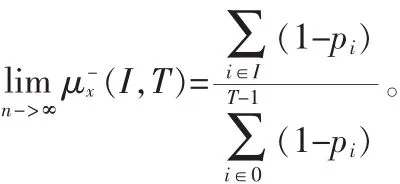

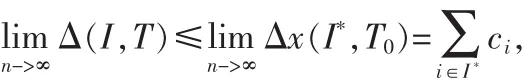
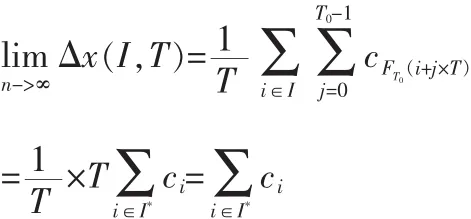
3.3 周期模式挖掘算法
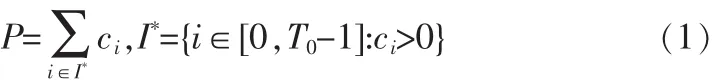
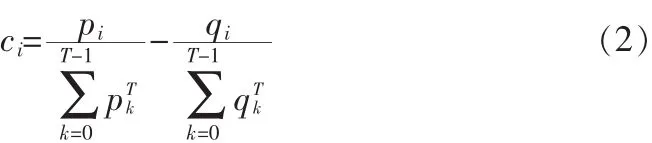
4 實驗及結果分析


5 結 論