區域霧霾環境的優化監測探究
□凌 龍 錢學明
近年來,隨著經濟規模的迅速擴大和工業化進程的加快,大氣污染日趨嚴重。2013年1月,我國中東部地區相繼出現大范圍霧霾,城市能見度降低,空氣質量差,對交通安全和人們的日常生活造成了嚴重影響。目前,霧霆天氣的發生已經無法避免,如何減少霧霾天氣造成的損失和傷害,降低霧霾天氣污染物對人們身體健康的毒害,成為眾多專家學者關注的焦點[1~2]。不難發現,霧霾問題的解決在于預防和治理,而其基本任務是要迅速建立有效的監測系統。為此,我們需要解決兩個基本問題。其一,天氣狀況的預報依賴于模型,霧霾作為一種天氣現象,需要建立符合其內在規律的數學模型。其二,霧霾環境的有效監測在于能否確定最佳的測量時間。研究發現,大氣污染呈現為一個擴散輸運過程,其特點是系統的狀態不但依賴于時間而且依賴于空間,且具有復雜的動態特性。陳英杰等[3]通過擴散過程的動力學分析,建立了大氣污染的三維反應擴散模型。基于此類模型,Qian[4]進一步討論了擴散過程中移動控制下的優化測量方案。
一、區域霧霾環境的模型描述
本文考慮一類線性反應擴散方程描述區域霧霾的天氣

其中x 表示一維空間的位置,x∈[0,ι],時間t∈R+,N(x,f)表示霧霾環境中t 時刻x 處污染物的濃度,ɑ >0 為擴散系數。系統滿足初始條件N(x,0)=N0(x)和Dirichlet 邊值條件N(0,t)=N(l,t)=0。φ(x)>0 為吸收衰減函數,且φm≤φ(x)≤φM。
二、模型的穩定性分析
定理:區域霧霾環境的線性擴散模型(1)在其初、邊值條件下,若滿足α >0 成立,則(1)是全局指數穩定的。
證明:對于動態系統(1),我們取Lyapunov 函數如下

計算沿系統(1)軌跡的時間導數

以下討論系統的指數穩定性。為此,考慮

于是,eαtV(t))=V(0)+(eαtV(t))ds≤V(0),不難計算得到V(t)≤e-atV(0)。

因此,‖N(x,t)‖2≤ρ0e-at。即系統(1)是全局指數穩定的。
三、測量時間優化方案
事實上,霧霾天氣的產生來源于大氣氣溶膠的影響[5]。研究表明,大氣氣溶膠的測量可用于霧霾的定量。換言之,我們通過測量大氣氣溶膠來間接確定霧霾的濃度。
因此,對于區域霧霾的線性擴散模型,系統的測量輸出可以寫成以下形式。
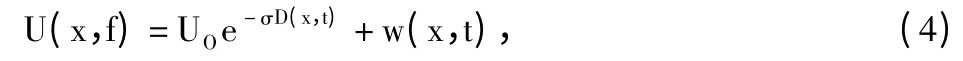
其中U(x,t)為儀表測量輸出的電壓值,U0為太陽地外常量,σ 為大氣中所含氣團量,一般取σ=1/sinθ(θ 是太陽光入射到地面的夾角),D(x,t)為氣溶膠光學厚度,與霧霾濃度N(x,t)線性相關,即D(x,t)越大,N(x,t)越大,反之亦然。因此,D(x,t)可用來表征霧霾濃度N(x,t)。w(x,t)表示不同位置的測量噪聲。假設w(x,t)為獨立分布的白噪聲,且滿足E{w(x,t)}=0,E{w(s,t0)wT(x,τ)}=I。
為了得到系統的最佳測量時間,我們將儀表的測量輸出在t=t0的領域內線性化。利用泰勒公式,則(4)式可寫為U(x,t)=g(x,t0)+t=t0(t-t0)+o(ρ)+w(x,t),其中,g(x,t)=U0e-σD(x,t)。
考慮到g(x,t0)+t=t0t0與t 無關,且忽略高階項,則可近似寫為

其中h(x,t0)=|t = t0= -|t=t0。
設輸出誤差平方準則函數為

利用加權最小二乘法計算可知,時間估計誤差的方差最小時,時間估計值滿足:

通過以上分析可知,μ 與最佳測量時間t0有關,且其取最大值時時間估計誤差的方差最小。因此,使μ 取得最大值的t0即為所求最佳測量時間。
四、數值例子

圖1 霧霾濃度的時空分布
系統在[0,1]上測量輸出為U(x,t)=U0e-σD(x,t)+w(x,t)。設最佳測量時刻為t1,我們考慮μ(t1),計算可知當t1=0.02時,μ 最大。于是,t1=0.02 為系統的最佳測量時間。
[1]張軍英,王興峰.霧霾的產生機理及防治對策措施研究[J].環境科學與管理,2013,38(10):157~159
[2]周廣強,陳敏,彭麗.霧霾科學監測及其健康影響[J].科學,2013,65(4):56~59
[3]陳英杰,劉玉良,劉萍.三維大氣污染反應擴散方程模型[J].哈爾濱師范大學自然科學學報,2014,5:1~3
[4]X.Qian.Optimal monitoring in reaction-diffusion model of the atmospheric pollution[J].Journal of Simulation,2015,3(2):3~6
[5]何杰,董國波,李英姿,等.使用太陽光度計測大氣霧霾[J].物理實驗,2013,33(11):1~3

