基于B樣條的五軸聯動加工刀軸運動的優化

趙一帆 沙 玲 張鵬舉

(1.上海工程技術大學機械工程學院，上海 201620；2.美鉆能源科技(上海)有限公司，上海 201620)

在五軸聯動加工中，多個方向上刀軸的變化都將導致刀軸運動加工不平穩，影響加工精度和切削質量。而隨著現代制造業越來越高的要求，要保證高效率、高質量的零件加工，五軸聯動加工中刀軸運動的平穩準確性變得越來越重要。目前在實際生產中，特別是在五軸聯動這種高速率、高精度的加工過程中，為了保證整個加工過程平穩、準確，刀軸的最大角速度、角加速度都要減速以保持在指定值之下[1]。因此，如果對刀軸的運動沒有任何優化調整將影響加工切削性能和幾何工件的精度。

目前五軸聯動加工中，刀軸運動方向的修改和加工路徑的優化算法[2～4]通常集中在最小化的基礎上來調整，雖然基本建立了基于B樣條的整個刀軸運動加工路徑，但對最大角速度、最大角加速度這些最大化運動參數以及不同條件的運動約束對整個刀軸運動加工過程的影響明顯考慮不足，因為刀軸的最大角速度及角加速度等運動特征值都必須低于指定值，即使是相同的刀軸加工路徑，也會產生不同的運動特性，造成工件整體加工質量的差異。對此，筆者在B樣條曲線的基礎上，根據刀軸加工過程中的這些運動約束條件提出了一種優化五軸聯動加工中刀軸運動的方法。

對刀軸運動進行優化調整，首先要建立刀軸表面的雙重B樣條曲線，然后沿著刀軸運動加工路徑分析刀軸的具體運動約束條件，再根據整個加工過程中刀軸的最大角速度、角加速度來對刀軸的運動進行調整，從而得到一條修正后的刀軸表面雙重B樣條曲線，最后通過修正后的刀軸表面雙重B樣條曲線找到刀軸運動過程中需要轉換的點進行優化，即可實現對整個刀軸運動過程的優化。

1 刀軸表面雙重B樣條曲線的建立①

為了減少大量離散的刀軸運動數據點，在五軸聯動加工中，可用一個相同數據格式的雙參數曲線P(u)和D(u)來表示連續刀軸的運動路徑，曲線P(u)代表刀尖曲線，D(u)代表與刀尖曲線P(u)相關聯，刀軸上另一個點的軌跡曲線。

目前，連續刀具軌跡段通常是由非統一有理樣條(NURBS)來表達，它已成為計算機輔助設計和計算機輔助制造系統中的一個標準曲線[5,6]。將NURBS曲線的權重設為1，它就變成了B樣條曲線，五軸聯動加工中刀軸軌跡的雙參數曲線即可定義為相同參數的B樣條曲線，用n+1個控制點和節向量[u0,…,un+k+2]來表達，這樣刀尖曲線P(u)的路徑參數u即可作為規范化弧長參數給出[7]。在實際操作中，對于給定的采樣點，路徑參數可能是第一個由累積弦長參數化簡得來的，然后在相應的參數位置，根據真實的擬合曲線長度，這個參數可以進一步修改為近似弧長參數，如果路徑位移參數是s，刀尖曲線的長度是L，則歸一化弧長參數為u=s/L，那么P(u)和D(u)這兩條B樣條曲線可以表示為：

(1)

其中Pi、Di代表控制點，Ni,k(u)是B樣條的基函數。

對于每個參數的位置u，刀軸的單元定位向量C(u)=(Cx(u),Cy(u),Cz(u))可以表示為：

C(u)=[D(u)-P(u)]/‖D(u)-P(u)‖

(2)

結合式(1)、(2)可進一步表示為：

在構建B樣條曲線的過程中，對于每一個參數u，如果距離參數‖D(u)-P(u)‖與一個少許偏差的長度h對等，即可簡化操作，使刀軸矢量變為：

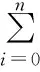
確定了刀軸運動路徑的幾何變量與運動變量的關系后，考慮五軸聯動加工中刀軸同步、耦合的平移和旋轉運動對刀軸運動方向的影響，建立的刀軸表面雙重B樣條曲線如圖1所示。

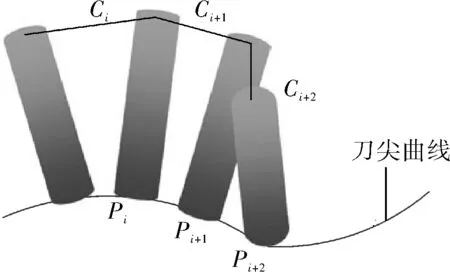
圖1 刀軸表面的雙重B樣條曲線

2 按最大角速度、角加速度調整刀軸運動

為了獲得良好的切削性能，刀軸的最大角速度、角加速度必須限制在指定值內。作為初始條件，刀具的進給速率應該首先定義在整個刀具運動路徑段，依據B樣條確定了刀軸運動路徑后[8,9]，刀具的進給速率也應使用B樣條進行定義：

(3)

此時還應讓節向量、曲線控制點的數量與刀軸運動路徑對應。雖然刀具的進給速率有時不同于它在加工代碼中的速率，但是根據連接空間和笛卡爾空間的聯系，可以將其中一個轉換成另外一個[10]，從而得到沿刀具運動路徑的切向加速度：

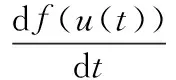
(4)

從規范化的弧長參數u=s/L得知，s是在位置u的真正弧長，L是刀尖路徑的總長度，結合式(4)可進一步得到切向進料加速度：

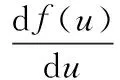
當然，根據以上公式的調整并不足以優化整個刀軸的運動，還必須根據加工過程中的最大角速度、角加速度來對刀軸的運動進行調整。給定一個旋轉角Δθ、路徑參數u，刀軸即可定位為任意連續的錐形表面，如圖2所示。

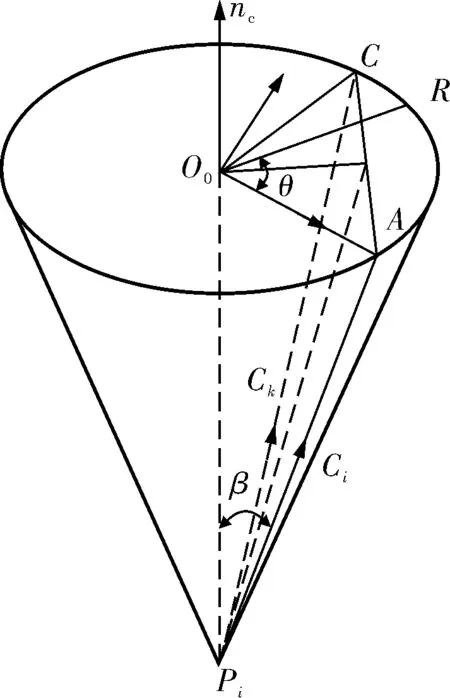
圖2 刀軸錐形表面示意圖

為了確定一個最適合的錐形表面，要根據相鄰刀軸位置的關聯點，給定一個在刀軸路徑點P(ui)上的刀軸矢量Ci，錐形表面的旋轉角Δθ可由下式得出：

[X-P(ui)]Ci=‖X-P(ui)‖cosΔθ

如果路徑參數ui+1上的刀軸矢量增加Δu變成Ci+1，刀軸在線性變化的情況下，路徑參數ui+1通過點(P(ui),Ci)和點(P(ui),Ci+1)就可以表示為：

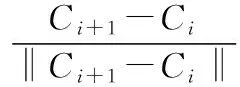
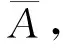
根據以上條件，得出調整后的刀軸表面雙重B樣條曲線(圖3)。

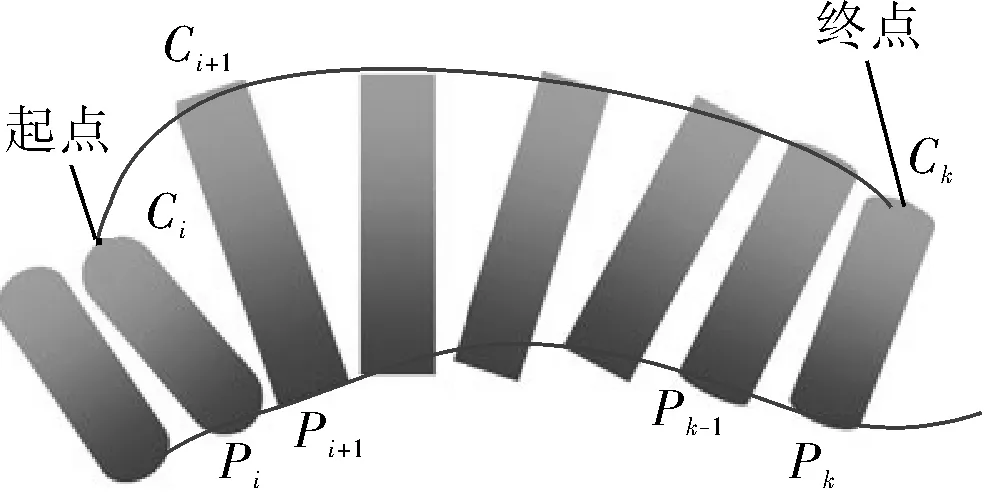
圖3 調整后的刀軸表面雙重B樣條曲線

3 獲取刀軸運動過程中的轉換點

根據上文得出調整好的刀軸表面雙重B樣條曲線后，根據最大角速度和角加速度的約束可重新分配新的刀軸定位數據，保持刀軸運動過程中基本的關鍵點不變，則與這些關鍵點相關聯的點即可進行優化調整，得出使整個調整距離最小的點即刀軸加工過程中的轉換點。如圖4所示，在Ci點和Cj+1點轉換，改變刀軸運動即可保證Ci+1到Cj的距離最小，按轉換點的位置調整刀軸的運動即可提高整個加工過程的連續平穩性，進一步優化五軸聯動加工的準確性。

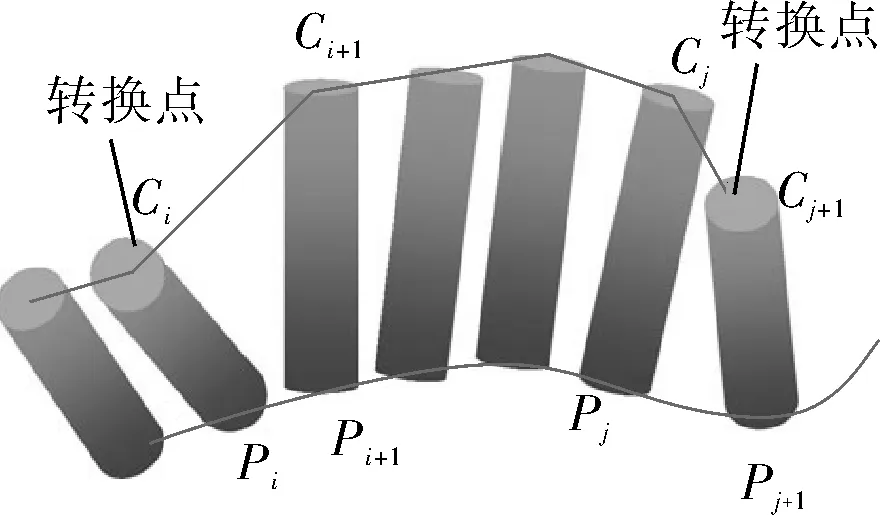
圖4 獲取轉換點后的刀軸運動曲線

4 結束語

基于刀軸運動整個過程中的運動約束條件，將刀軸定義為可以深入分析的連續錐形表面，得到了一種更準確的刀軸運動曲線，從而提出了一種新的調整五軸聯動刀軸運動的優化方法，對進一步深化五軸聯動的有關研究，達到高質量、高效率的目標提供了具有實際意義的參考。

[1] 張政潑，譚學東.五軸聯動機床的結構性能分析與設計探討[J].裝備制造技術，2009,(10):5～8，11.

[2] 張瑩，張定華，吳寶海，等.復雜曲面環形刀五軸加工的自適應刀軸矢量優化方法[J].中國機械工程，2008,19(8):945～948.

[3] 樊留群，齊黨進，沈賦，等.五軸聯動刀軸矢量平面插補算法[J].機械工程學報，2011,47(19):158～162.

[4] 羅明，吳寶海，李山，等.自由曲面五軸加工刀軸矢量的運動學優化方法[J].機械工程學報，2009,45(9):158～163.

[5] 姚哲，馮景春，王宇晗.面向五軸加工的雙NURBS曲線插補算法[J].上海交通大學學報，2008,42(2):235～244.

[6] 張小明，朱利民，丁漢，等.五軸加工刀具姿態球面NURBS曲線設計及優化[J].機械工程學報，2010,46(17):140～144.

[7] 陳偉，殷蘇民.五軸聯動數控激光加工系統的空間曲線B樣條插補算法研究[J].機床與液壓，2004,(1):53～55.

[8] 劉建偉，王衛英，曾禮平.高速數控加工復雜曲線的刀具軌跡計算方法[J].輕工機械，2012,30(2):79～81.

[9] 陳良驥，程俊偉，王永章.環形刀五軸數控加工刀具路徑生成算法[J].機械工程學報，2008,44(3):205～212.

[10] 任斐.基于坐標映射的復雜曲面五軸加工關鍵技術研究[D].遼寧：大連理工大學，2011:10～65.

[11] Sun Y W, Bao Y R,Kang K X,et al.A Cutter Orientation Modification Method for Five-axis Ball-end Machining with Kinematic Constraints[J].The International Journal of Advanced Manufacturing Technology,2013,67(9-12):2863～2874.

[12] 陳良驥，劉元朋.五軸加工中局部曲率的計算及其應用研究[J].制造技術與機床，2009,(1):82～85.