氣相聚乙烯工業裝置多牌號質量指標魯棒濾波估計
周 鑫 趙 眾 孫 康
(1.北京化工大學信息科學與技術學院,北京 100029;2.中國石油化工股份有限公司北京化工研究院,北京 100013)
在氣相聚乙烯[1]的工業生產過程中,有兩個非常重要的產品指標——熔融指數和密度,它們能實現對產品質量指標的精確估計,有助于提高聚乙烯工業裝置優化控制的結果。目前工業應用的在線測量儀表存在不準確的問題,聚乙烯產品質量主要通過定時采樣得到分析數據,再根據分析數據來調控以實現對質量指標的控制。這樣的操控方式使得聚乙烯生產過程中產品質量會出現波動,嚴重時可能造成停車。在實際的氣相聚乙烯工業生產中,氣相法生產聚乙烯的牌號有多種,以此來滿足市場對不同產品的需求,在實際生產過程中常常需要進行多種牌號間的相互切換。牌號切換會造成聚乙烯產品質量的波動,同時也會造成定時采樣分析數據過程不準確。筆者針對該生產過程進行質量指標的在線估計,有助于提高企業的產品質量和經濟效益。
1 聚乙烯質量指標動態模型①
在Unipol工藝的聚乙烯工業裝置中,通常用熔融指數MI代表聚合物的分子量,密度Den代表共聚組成。實際生產過程中,聚合物的分子量受到諸多因素的影響,當催化劑確定后,產品的質量主要受以下因素影響:聚合溫度、氫氣/乙烯比、共聚單體/乙烯比。一般提高溫度,可以加快鏈轉移反應,使聚合物分子量下降,熔融指數升高;氫氣作為鏈轉移劑加入反應體系中主要用來控制熔融指數,氫烯比的提高,使得樹脂分子量降低而樹脂的熔融指數隨之提高。同時,熔融指數還與聚合溫度和共聚單體的濃度有關。聚合溫度關系到催化劑的活性,共聚單體的加入,可以增加聚乙烯分子鏈的支鏈數目。因此,熔融指數主要由氫氣濃度進行調節,其他參數可作為熔融指數MI的微調參數。建立熔融指數機理模型如下[2]:
lnMIc(i+1)=fr(i)lnMIc(i)+[1-fr(i)][θ0+
(1)
聚合物的密度取決于聚合物鏈的結構參數,可用一般的經驗公式表示[3]:
Denc(i+1)=fr(i)Denc(i)+[1-fr(i)]·
(2)
根據實際經驗,式(2)可進一步簡化為:
Denc(i+1)=fr(i)Denc(i)+[1-fr(i)]·
(3)
其中,θ0~θ8為模型參數,[C2]、[Cx]、[H2]分別為乙烯濃度、共聚單體濃度和氫氣濃度,fr=exp(-Δt/τ),lnMIc、Denc分別為lnMI、Den累積值,Δt為采樣時間,τ為顆粒在反應器中的停留時間。
2 質量指標在線魯棒濾波估計
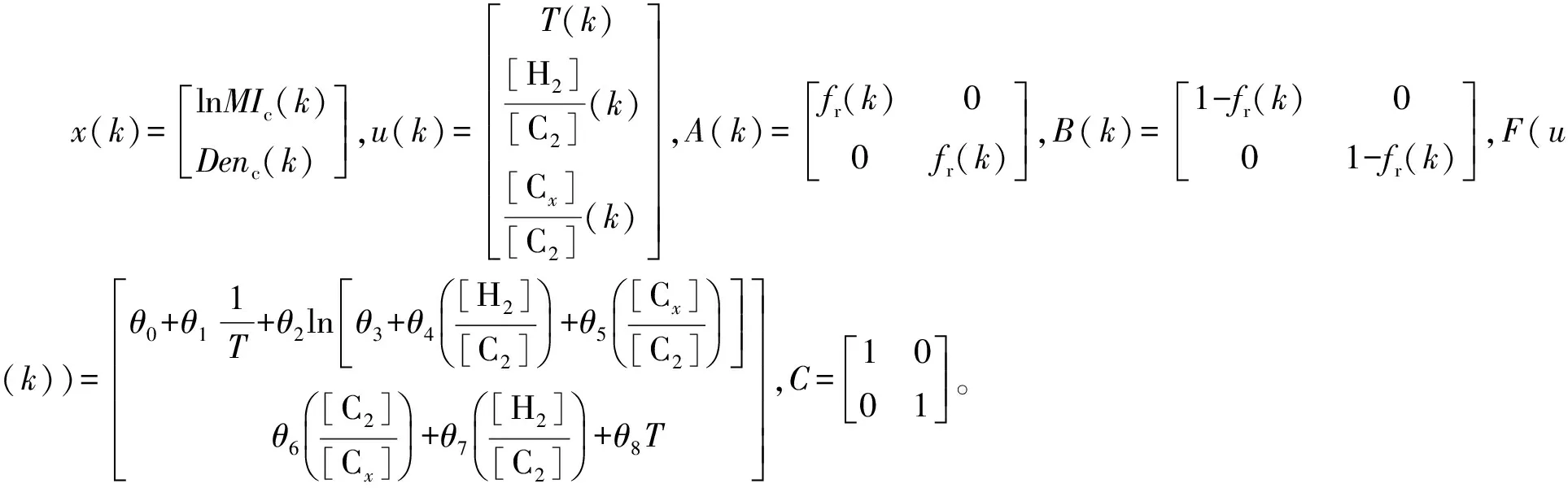
用下面的非線性動態模型來描述式(1)、(3)的質量指標預測模型:
x(k+1)=A(k)x(k)+B(k)F(u(k))y(k)=Cx(k)
(4)
其中x為狀態向量,x∈Rn;u為控制輸入向量,u∈Rq;y為輸出向量,y∈Rm;F為辨識得到的非線性穩態函數,F∶Rq→Rn;C為測量矩陣,C∶Rm×n。
實際非線性動態過程可表示為:
x(k+1)=f(x(k),u(k))+ξ1(k)y(k)=Cx(k)+ξ2(k)
(5)
其中f∶Rn×Rq→Rn為未知非線性函數,ξ1(k)、ξ2(k)分別為n維和m維高斯白噪聲向量,且具有如下的統計性質:
Eξ1(k)=Eξ2(k)=0,E[ξ1(k)ξ2(k)T]=0
(6)
E[ξ1(k)ξ1(j)T]=Qδk,j,E[ξ2(k)ξ2(j)T]=R(Δ)δk,j
(7)
其中Q為模型噪聲方差,是正定對稱矩陣;E為數學期望符號;δk,j為Kronecker函數;R(Δ)為測量噪聲方差,具有如下不確定性:
R-1(Δ)=R-1+MΔN+NTΔMT
(8)
其中Δ∈{Δ∶‖Δ‖≤1},表征多牌號切換時由于工藝變動引起的不確定性。
濾波估計如下[4]:
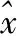
(9)
其中K(k)為濾波器增益矩陣,K(k)∈Rn×m。
定義 預測模型的真實最大逼近偏差為:
ef≡‖f(x(k),u(k))-A(k)x(k)-B(k)F(u(k))‖∞
(10)
估計誤差偏差為:
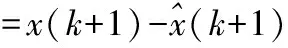
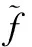
K(k)ξ2(k)
(11)
預測模型誤差為:
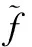
(12)
估計誤差協方差陣為:
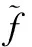
[A(k)-K(k)C]ρ(k)[A(k)-K(k)C]T+QI+K(k)R(Δ)KT(k)
(13)
引理1d∈Rn為一列向量,I為單位陣,有ddT≥0;dTdI≥ddT。
由引理1,則以下的矩陣不等式成立:
(14)
≤[A(k)-K(k)C]ρ(k)[A(k)-K(k)C]T+nef2I
(15)
把式(13)化為:
ρ(k+1)≤2nef2I+2[A(k)-K(k)C]P(k)[A(k)-
K(k)C]T+QI+K(k)R(Δ)K(k)T
(16)
取P(k+1)為ρ(k+1)的上限估計,其中P(0)≥ρ(0),且P(k+1)滿足遞推關系:
P(k+1)=2nef2I+2[A(k)-K(k)C]P(k)[A(k)-
K(k)C]T+QI+K(k)R(Δ)K(k)T
(17)
易證:P(k+1)≥ρ(k+1)。
通過極小化誤差協方差上限大小,優化得到狀態估計器,其中估計器增益K(k)和誤差協方差上限矩陣P(k+1)滿足:
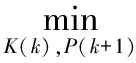
(18a)
2nef2I+2[A(k)-K(k)C]P(k)[A(k)-K(k)C]T+
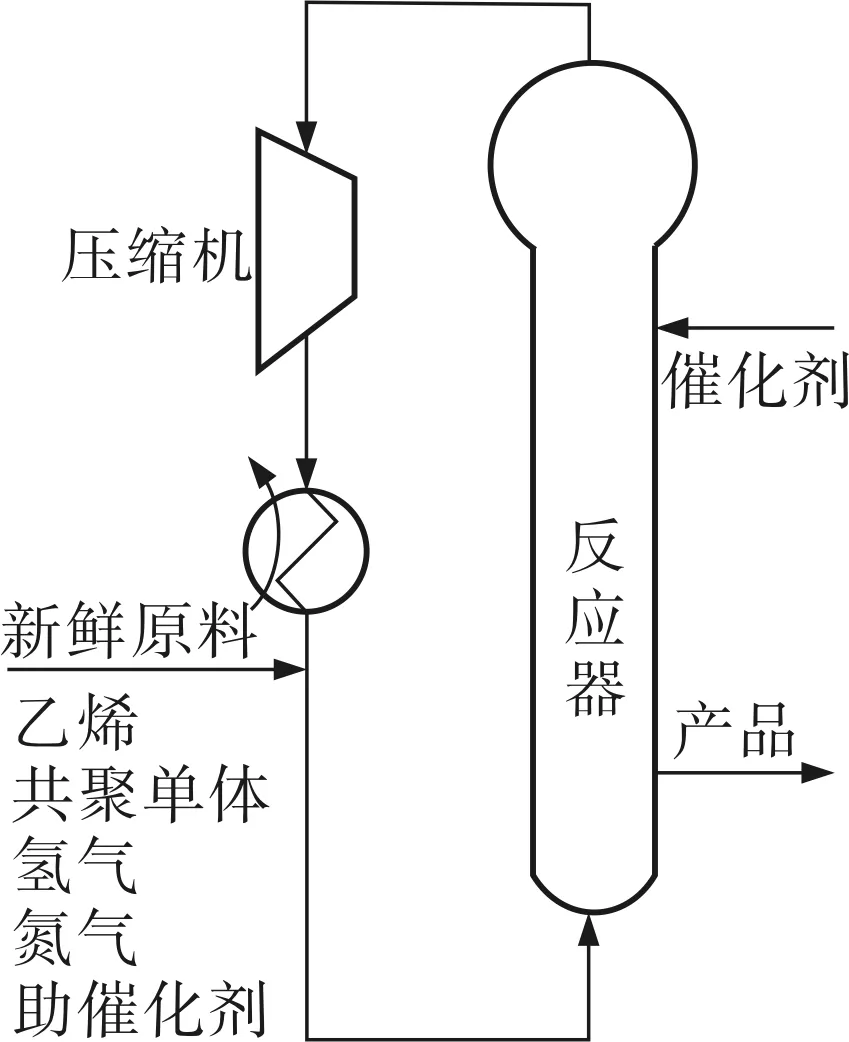
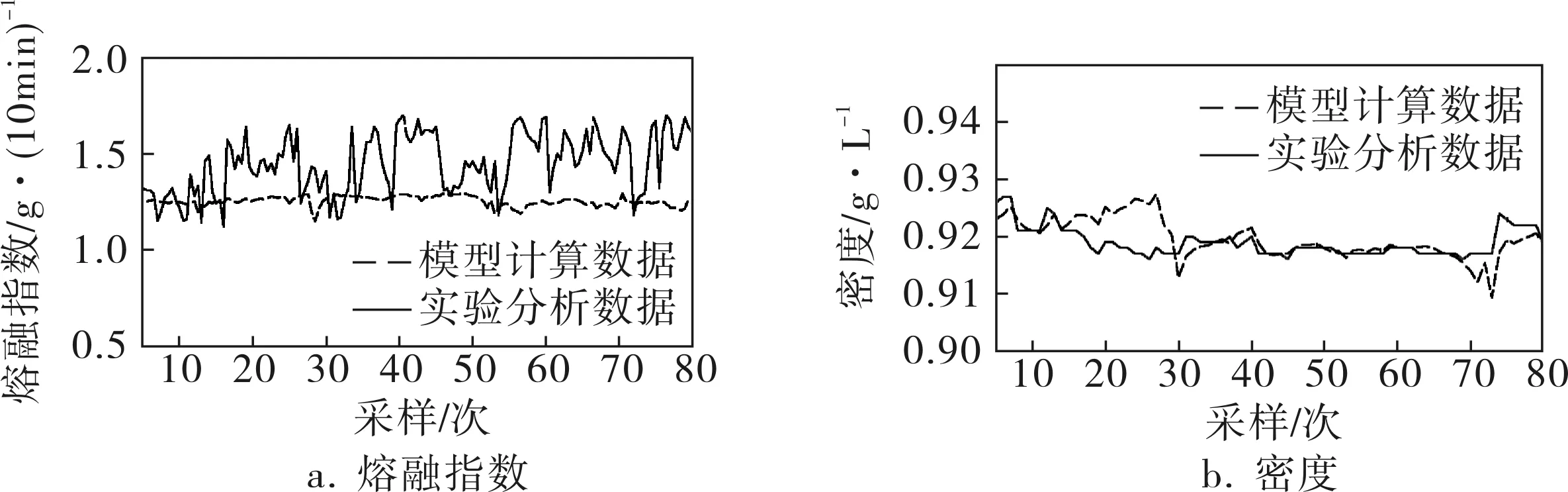
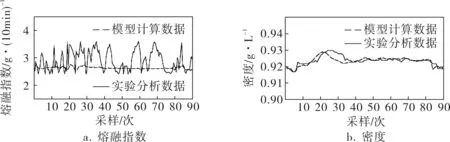
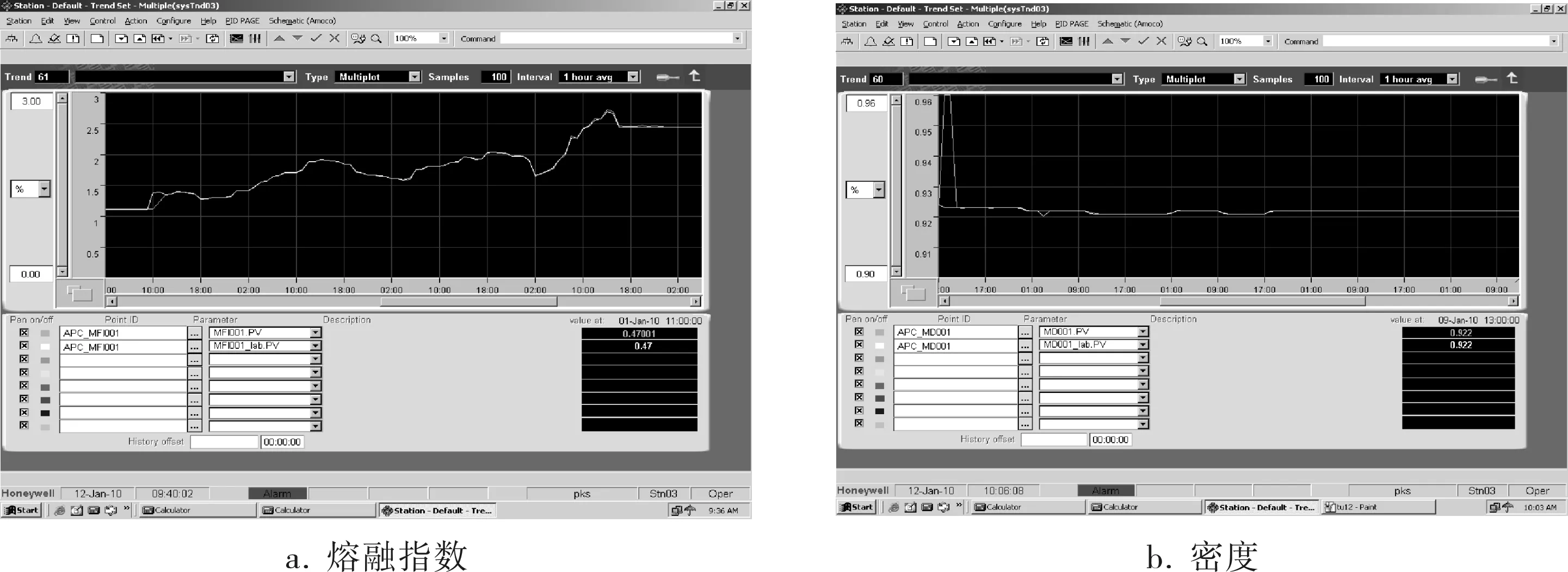
QI+K(k)R(Δ)K(k)T (18b) 其中‖P(k+1)‖∞為估計誤差協方差上限的無窮范數。 (19) 引理3[6]給定具有適當維數的實矩陣F=FT、M、N,當且僅當存在λ使得下式成立: (20) 則對于所有的Δ,‖Δ‖≤1,F+MΔN+NTΔTMT>0成立。 定理1 優化問題式(18)可用如下線性矩陣不等式(LMI)求解: (21) (22) 證明 式(18b)可轉化為: (23) 由引理3,式(23)可轉化為: (24) 將R-1(Δ)不確定形式代入,得: (25) 由引理3,得: (26) 綜上,基于LMI的濾波器增益矩陣K(k)的遞推算法如下: a. 給定初始誤差協方差矩陣P(0)、噪聲方差Q、R(Δ)、初始狀態x(0); b. 在采樣k時刻,求解式(21)、(22),得到最壞情況下的遞推矩陣P*(k+1)和K(k); c. 根據協方差上限遞推矩陣(17),計算k+1時刻誤差協方差上限矩陣P(k+1),重復步驟b。 將筆者提出的魯棒濾波方法應用在中石化某氣相法聚乙烯工業生產裝置上,生產工藝流程如圖1所示。乙烯、丁烯(或己烯)、氫氣、氮氣和其他惰性氣體一起被加入反應系統組成循環氣體。循環氣體通過反應器,主要是流化聚乙烯顆粒,同時把部分乙烯聚合(轉化率為1%~2%)。循環氣體從反應器出來之后先進入循環氣體壓縮機,再經過換熱器,最后再重新回到循環反應器中。精制乙烯、氫氣、丁烯(或己烯)、三乙基鋁助催化劑從流化床循環管路進入聚合系統。把催化劑直接注入到流化床反應器內,反應器的出料機構把聚合物產品輸出,并且保持反應器的料位高度恒定。 圖1 氣相聚乙烯生產工藝流程簡圖 設定質量指標預測模型辨識目標函數為: (27) 運用粒子群優化算法[7],選擇牌號DGM-1815的數據,通過求解式(27),得到質量指標預測模型參數(表1),模型最大偏差和均方根誤差見表2,模型辨識效果如圖2所示。由圖2可以看出,所得到的模型變化趨勢與實際生產過程中質量指標的變化趨勢相符。 表1 質量指標預測模型參數 表2 模型辨識與泛化效果 圖2 DGM-1815熔融指數和密度的預測模型與實際數據比較 獲得模型參數后,筆者對不同牌號的DGM-1830進行了模型參數泛化驗證,驗證效果如圖3所示。模型最大偏差和均方根誤差見表2。從圖3和表2可以看出,所得動態模型反映了實際生產過程中熔融指數和密度的變化趨勢,但對于多牌號的泛化會引起模型預測誤差的顯著增加,因而根據實驗室分析數據進行濾波修正是非常必要的。 圖3 DGM-1830熔融指數和密度的預測模型與實際數據比較 美國聯碳校正算法為: (28) EMXf=λEXX+(1-λ)EMXfold (29) 其中EMX為瞬時模型偏差;EMXfold為上一時刻濾波后的模型偏差;λ為模型偏差的濾波系數(缺省取0.4~0.8)。此外還需要一些條件來對校正進行選擇:RX>8或EMX>3σX。所提方法與美國聯碳應用比較如圖4所示。最大方差和均根誤差比較結果見表3。從圖4可以看出,所提方法的質量指標曲線比美國聯碳校正方法的質量指標曲線更加貼近實際值,有效地修正了多牌號模型預測的偏差。 表3 校正效果比較 所提方法已在中石化某氣相聚乙烯工業裝置上成功投用,DCS上實際投用效果曲線如圖5所示。從投用效果圖可以看出,所提方法真實反映了多牌號的質量指標變化趨勢,達到了實時估計的目的,為質量指標閉環優化控制提供了良好的條件。 圖5 熔融指數和密度的DCS實際投用效果 針對氣相聚乙烯工業裝置多牌號質量指標實時估計的復雜性,在聚乙烯工業裝置質量指標實時預測模型的基礎上,提出了一種氣相聚乙烯工業裝置多牌號質量指標魯棒濾波器設計方法。利用該方法根據實驗室分析數據反饋修正模型預測并實時估計質量指標。該方法將模型逼近偏差顯式地引入到濾波器設計中,并考慮了由多牌號切換引起的工藝不確定性,利用LMI和最小方差估計原理進行濾波器增益的實時求解。該方法在氣相聚乙烯工業裝置上的應用結果和與美國聯碳技術的應用對比證實了其有效性和可行性,為實現氣相聚乙烯工業裝置多牌號質量指標的閉環優化控制創造了良好的條件。 [1] 鄧哲文.氣相流化床法聚乙烯工藝技術比較[J].化工設計,2006,16(4):9~13. [2] McAuley K B,MacGregor J F.A Kinetic Model for Industrial Gas Phase Ethylene Copolymerization[J].AIChE Journal,1990,36(6):837~844. [3] Debling J,Kuijpers F,Ray W H.Dynamic Modeling of Product Grade Transition for Olefin Polymerization Process[J].AIChE Journal,1994,40(3):506~513. [4] 趙眾,馬博.大型聚乙烯工業裝置質量指標的次優強跟蹤濾波估計[J].化工學報,2008,7(15):1635~1639. [5] Boyd S,Ghaoui L EI,Feron E.Linear Matrix Inequalities in Systems and Control Theory[M].Philadelphia,PA:SIAM,1994. [6] Calafiore G,Ghaoui L EI.Minimum Variance Estimation with Uncertain Statistical Model[C].Proceedings of the 40th IEEE Conference on Decision and Control.Orlando, Florida USA:IEEE,2001:3497~3499. [7] Ratnaweera A,Halgamuge S K,Watson H C.Self-organizing Hierarchical Particle Swarm Optimizer with Time-varying Acceleration Coefficients [J].IEEE Transactions on Evolutionary Computation,2004,8(3):240~255.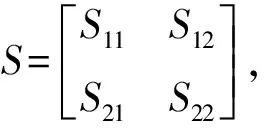
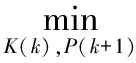
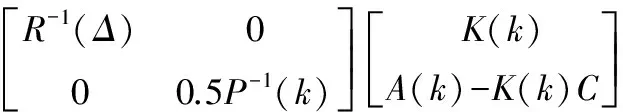
3 實際應用

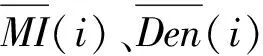


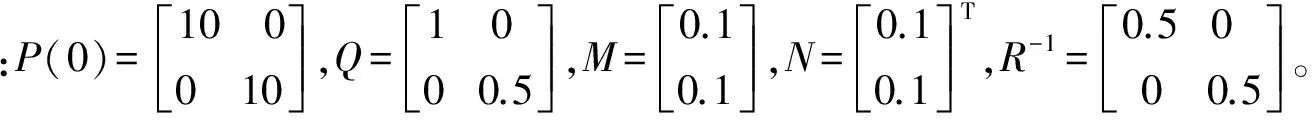
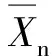

4 結束語

