預測控制算法在硝酸溫度控制中的應用研究

劉新夢 林紅權,2 曾雋芳,2 馬增良

(1.中國科學院自動化研究所,北京 100190；2.北京三博中自科技有限公司，北京 100190)

硝酸廣泛應用于航天及化工等領域。工業硝酸生產過程中極為重要的控制環節是氧化爐氨空比與溫度的控制，氨空比與氧化爐反應溫度直接影響硝酸成品的質量，氨空比是整個硝酸生產過程中的關鍵。氧化爐作為氨氣與空氣混合反應的主要設備，其溫度是生產過程中極為重要的控制指標，加之溫度本身具有滯后性和非線性，采用傳統PID控制策略實現氧化爐溫度控制存在明顯的波動。 為此，以某實際雙加壓法硝酸生產工藝為背景，在分析氧化爐溫度特性的基礎上，提出采用模型預測的控制策略，并在建立氨空比與溫度模型的基礎上仿真分析了模型預測控制算法相比傳統控制算法的優勢。

硝酸的整個生產工藝流程如圖1所示，氨氣與空氣反應的主要設備為氧化爐。硝酸生產過程中，首先是氨空混合氣的制備，氨氣與空氣混合之后進入氧化爐反應制取NOx氣體。NOx氣體被送入漂白塔底部進行漂白，經過氧化氮精分離器、二次空氣加熱器、高壓反應水冷凝器后，最終進入吸收塔底部，與工藝水泵送至塔頂的工藝水逆流接觸反應生成硝酸。高壓反應水冷凝器生成的冷凝酸最終被送入氧化氮分離器[1～3]。

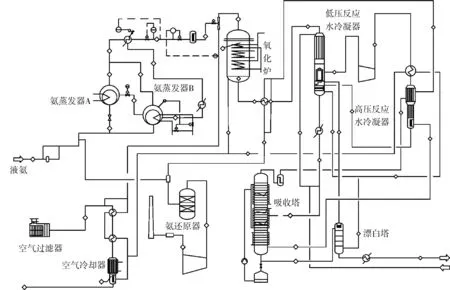
圖1 硝酸生產工藝流程示意圖

整套硝酸生產過程中，主要有3個關鍵控制點：氨氧化工藝指標、NOx吸收工藝指標和成品酸的質量。在此僅針對氨氧化工藝部分的控制進行研究。氨氧化工藝指標有：氧化爐溫度850～880℃、氨氧化壓力350～450kPa和氨空比9.35%～9.75%。

2 氨空比模型的建立

建立模型的基礎是獲得相應模型的數據。該工藝模型的數據是基于OPC協議通過WinCC與Matlab軟件得到的。具體實現方法是利用Matlab的OPC工具箱，WinCC作為OPC Server，Matlab作為OPC Client進行數據的實時采集與交換。氨空比模型參數的求取主要包含模型階次和模型參數的確定。采用階躍響應法，在氨空比為9.50%且現場生產較為平穩的情況下加入0.05%的階躍信號，測取氧化爐溫度變化，在此基礎上進行建模。

2.1 模型階次的確定

通過均值E(D)、方差Var(D)、最終預測偏差(FPE)和Best fit共同確定模型的階次。其中，均值E(D)和方差Var(D)分別為：

(1)

評價所建立的預測模型是否合適或可接受，通常有不同的標準。統計檢驗是評價模型預測效果的一個比較常用的辦法。統計檢驗的基本原理：首先由模型的使用者根據需要事先指定一個可接受的誤差標準數值e和一個小概率α，如果統計檢驗誤差D滿足P(|D|≤e)≥1-α，則模型被認為是可以接受的。如果α值很小，意味著模型產生的誤差D總體上將以很高的概率小于e，此時認為模型是可以接受的。

通過OPC協議得到現場的實時數據，對其進行建模，得到各個不同階次模型的輸出溫度與實際氧化爐溫度(表1)。

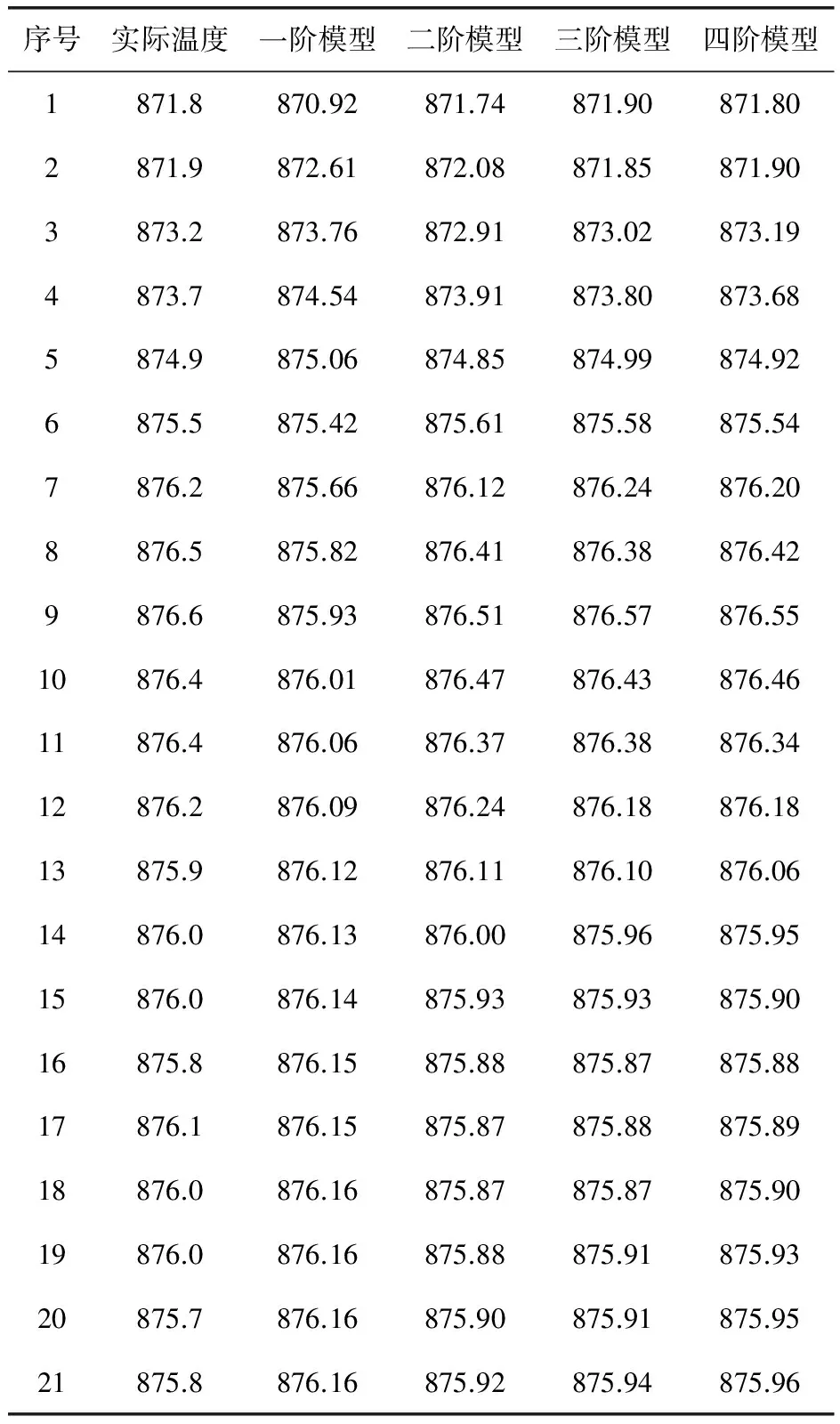
表1 實際溫度與不同階次下的 模型輸出溫度 ℃

從Best fit指標來看，一階模型的控制效果不是很理想，其他3個階次模型的效果大致一樣。依據FPE準則——節省原理(Principle of Parsimony)，即在提供的信息量基本相同的情況下，用盡可能少的參數建立模型[4]，3個階次模型都在可接受范圍內。

現對3個模型進行進一步篩選。采取模型統計檢驗進行分析，因為建模所用氧化爐溫度數據波動在0.4℃左右，故取誤差標準數值e=0.4和小概率α=0.05。查閱χ2分布表可知χ2(21)=32.67，故選擇接受三階與四階模型，考慮到數據的擬合程度，最終將氨空比模型定為四階，模型的性能指標見表2。

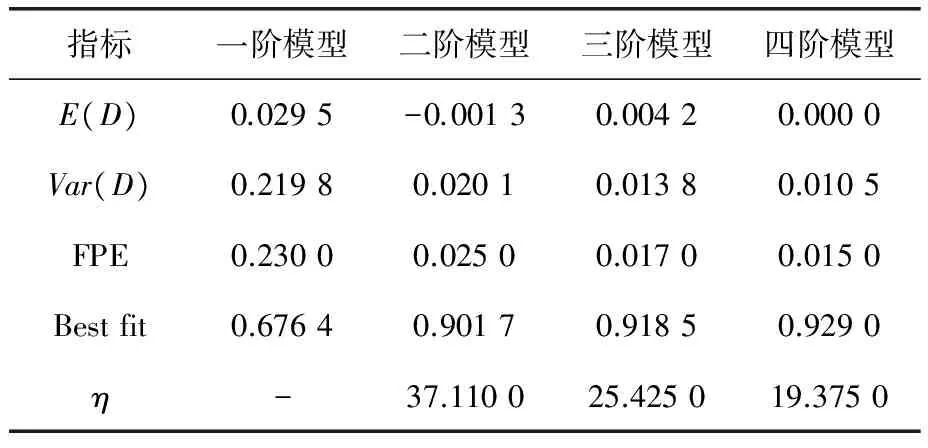
表2 模型的性能指標

2.2 模型檢驗

由于建立的氨空比模型為參數模型，在確定模型為四階的基礎上，選擇添加適當的零點。通過其相應階躍反應的超調比及調節時間等指標確定，選擇添加一個零點(加入滯后時間為3min)，最終氨(Y(z))空(U(z))比的參數模型為：

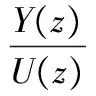
(2)

對數據進行建模的過程中，要檢驗模型的適用性。模型檢驗的實質是對模型殘差序列進行白噪聲檢驗。若殘差序列非白噪聲，說明一些重要信息未被提取，應重新設定模型。檢測方法為：選取工況穩定下的一組數據，利用氨空比數據測取模型輸出，對真實輸出與模型輸出的誤差進行白噪聲檢測。模型的擬合結果如圖2所示，可以看出，模型輸出能夠較好地反映氧化爐溫度的真實變化情況。經分析可知，誤差符合白噪聲檢驗，因此模型是滿足要求的。得到氨空比與氧化爐溫度的傳遞模型后，即可利用其進行模型預測控制研究。

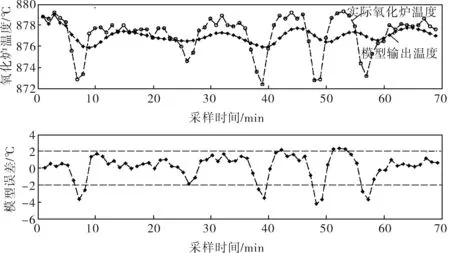
圖2 模型輸出、實際輸出與誤差曲線

3 模型預測控制

模型預測控制通常被簡稱為預測控制，是在建立各種不同模型的基礎上，采用在線滾動優化指標與反饋自校正的策略，力求有效克服受控對象的不確定性、時滯和時變影響，從而達到預期的控制目標——參考軌跡的輸入，并使系統有良好的魯棒性和穩定性[5，6]。預測控制的結構如圖3所示。

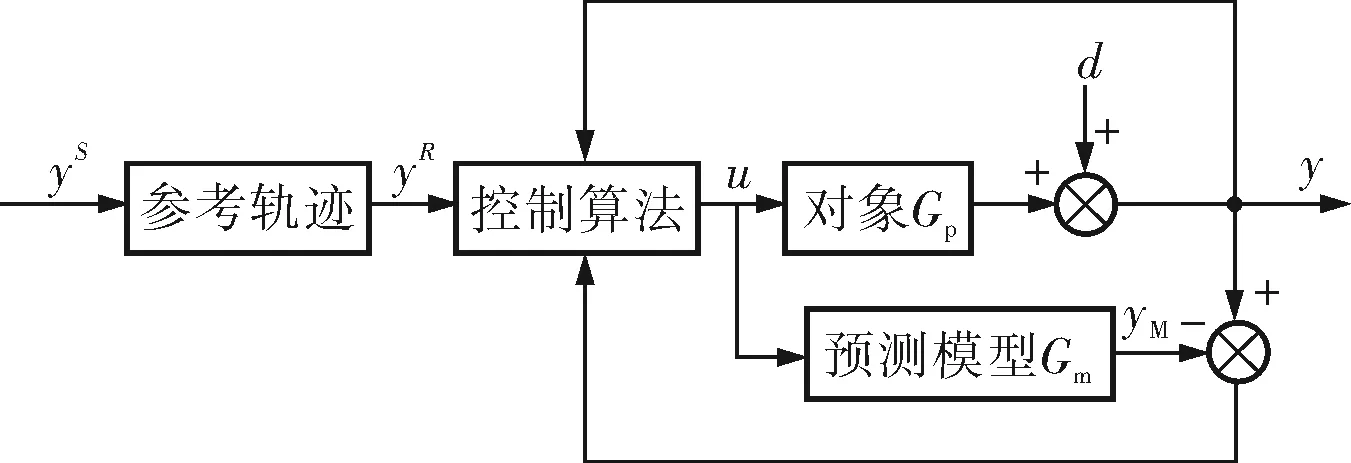
圖3 預測控制結構示意圖

預測控制算法一般包括3個部分，分別是模型預估、滾動優化和反饋校正。模型預估是展示系統未來動態行為的功能，任意給出未來的控制策略觀察對象在不同控制策略下的輸出變化，為比較這些控制策略的優劣提供依據；滾動優化不是一次離線進行，而是反復在線進行的；反饋校正可以在保持模型不變的基礎上對未來誤差進行預測并加以校正。

預測控制相比于傳統PID算法，是一種基于對象階躍響應的預測控制算法。傳統PID算法對溫度這種具有時延的控制對象不能取得良好的控制效果；而預測控制能有效解決時延問題，采用多步預估技術，并按預估輸出與給定值偏差最小的二次性能指標實施控制，是目前一種最優的控制技術[5，7～10]。

3.1 模型預估

動態矩陣控制是一種基于對象階躍響應模型的預測控制算法。動態矩陣控制利用對象階躍響應模型作為預測控制模型來獲得對象未來輸出的預測值。在工藝允許的情況下，利用階躍響應法得到響應模型。被控對象的階躍響應采樣值計算式為：

α(i)=α(iT),i=1,2,…,N

(3)

式中N——模型長度；

T——階躍響應的采樣周期；

α(i)——系統階躍響應在該時刻的幅值。

模型在k時刻的輸出是k時刻以前所有輸出增量的疊加，即：

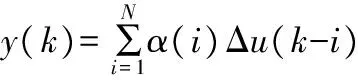
(4)

記當前時刻為k、預估步長L，如果當前和未來時刻的控制增量序列為Δu(k),Δu(k+1),…,Δu(k+L-1)，則未來時刻的輸出估計為：

yM=AΔu+s

(5)

其中A由對象動態響應系數構成，是維數為P×L的矩陣，為動態矩陣，易知AΔu為當前和未來時刻的控制對輸出的影響；s為過去的控制所產生的輸出[11]。

3.2 反饋校正

上述模型還未加入誤差與干擾，盡管模型預測輸出yM(k+j)能夠在k+j時刻接近期望輸出yR(k+j)，卻不能保證對象輸出yp(k+j)，因此需要對輸出預估值進行校正，從而得到更加準確的控制量。校正公式如下：

yc(k+j)=yM(k+j)+(y(k)-yM(k)),j=1,2,…,P

(6)

3.3 滾動優化

預測控制是一種最優控制策略，因為它以參考軌跡為優化目標，通過最優算法使其未來一段時間內的某項性能指標最小，控制作用序列采用預估偏差計算，但只有當前的控制作用是實際執行的。預測控制通常是在控制中設定一條參考軌跡，使輸出由當前值逐步過渡到設定值。通常采用的參考軌跡為一階指數形式，即：

yR(k)=y(k),yR(k+j)=αjy(k)+(1-αj)yS,

j=1,2,…,P

(7)

其中α=exp(-Ts/Tf)稱為柔化系數，yS為過程對象的設定值。

控制算法的任務是根據輸出預估值與輸出期望值的偏差來計算出用以施加的控制量，使對象的輸出盡可能接近期望的參考軌跡。性能指標用來表征控制算法的優劣，即：

J=eTQe+ΔuTRΔu

(8)

式中e——輸出預估偏差；

Q——誤差加權矩陣；

R——控制作用加權矩陣。

3.4 仿真結果

為了更準確地模擬實際工況，對過程輸出與控制輸出分別加入小幅波動信號。用Matlab進行仿真實驗，具體參數：控制步長L=2，預測步長P=4，誤差作用加權矩陣Q=0.9，控制作用加權矩陣R=0.9，一階慣性環節時間常數Tf=10，采樣時間Ts=1，模型長度N=40，過程對象設定值yS=876。所得模型輸出與預測控制輸出曲線如圖4所示，控制誤差與性能指標如圖5所示，控制增量曲線如圖6所示。依據實驗結果比較傳統PID控制與預測控制的控制效果，可見預測控制能夠取得良好的控制效果，控制增量基本保持不變，穩定情況下保持在10-4數量級左右，并沒有像實際現場那樣存在較大波動，同時也可以看到模型能夠很好地反應實際情況，性能指標也保持在0.0～0.2很小的范圍內，預測控制取得了較好的控制效果。因此，預測控制能夠很好地解決氧化爐溫度等具有純滯后對象的控制問題。

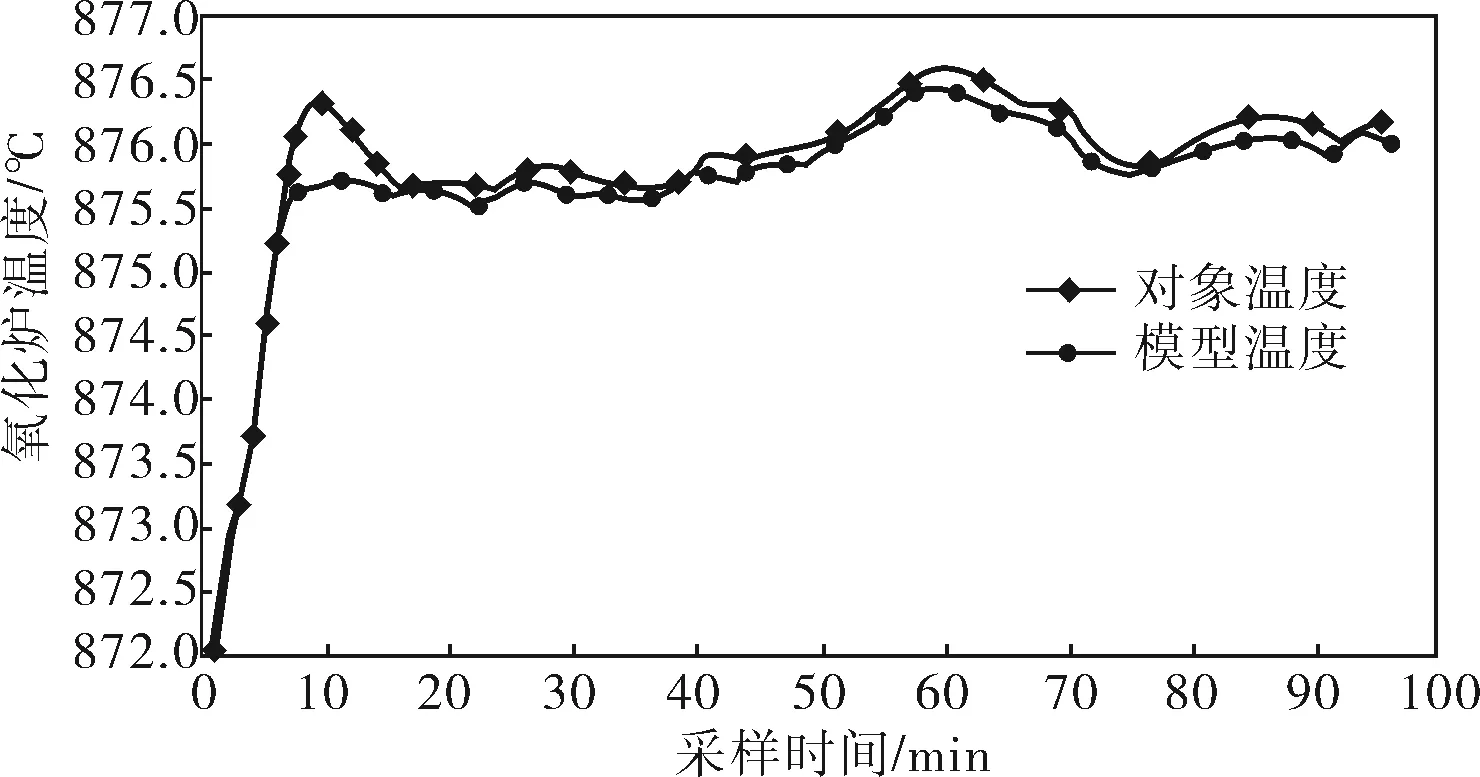
圖4 模型輸出與模型預測控制輸出曲線

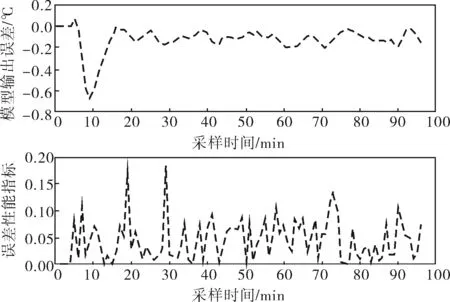
圖5 控制誤差與性能指標

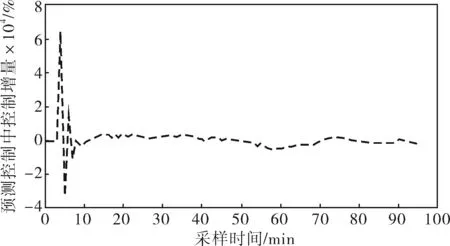
圖6 控制增量曲線

4 結束語

采用預測控制算法對硝酸生產中的氧化爐溫度進行控制。通過OPC協議讀取現場的實時數據，利用階躍響應法求得模型的離散傳遞函數，并對模型的精度進行檢驗。利用求得的模型來模擬現場實際工況，通過仿真比較傳統PID控制與預測控制的控制效果，可以看出預測控制效果在控制時延對象時能取得良好的效果。

[1] 李鑫.雙加壓法生產稀硝酸工藝的核心——四合一機組[J].新疆化工，2009，(4) ：20～21.

[2] 汪家銘.雙加壓法漸成我國硝酸生產的主流工藝[J].化學工業，2009，(6) ：73.

[3] 孫立輝.雙加壓法稀硝酸生產技術在我國的現狀及發展[J].氮肥技術，2008，29(2) ：44～51.

[4] 李進文.選擇藥物動力學模型的最終預測誤差準則[J].中國藥理學通報，1997，(3) ：85～86.

[5] 席裕庚,李德偉,林姝.模型預測控制——現狀與挑戰[J].自動化學報，2013，39(3)：222～236.

[6] 李永富.基于MATLAB混合仿真平臺的智能模型預測控制及其應用研究[D].天津：河北工業大學，2006.

[7] 高強,李航.基于單變量與多變量系統的模型預測控制研究[J].計算機工程與設計，2013，34(9) ：3266～3272.

[8] Li N,Li S Y,Xi Y G.Multiple Model Predictive Control for MIMO System[J].自動化學報，2003，29(4)：38～45.

[9] 劉富春,趙均,錢積新.多變量約束快速動態矩陣控制算法研究[J].浙江大學學報(工學版)，2005，39(5) ：68～71.

[10] 楊圓圓.模型模型預測控制研究與應用[D].大慶：大慶石油學院，2006.

[11] 黃德先，葉心宇,蘭建敏，等.化工過程先進控制[M].北京:化學工業出版社，2006：69～108.