基于動態圖的軟件水印算法

雷 敏，楊 榆，胡若翔，譚逢亮

(1.北京郵電大學信息安全中心，北京100876;2.災備技術國家工程實驗室，北京100876)

0 引言

軟件水印主要用于保護軟件的版權，分為靜態水印和動態水印[1－6]，其中動態軟件水印保存在程序的執行狀態中。在動態軟件水印算法中，最具代表性的是 CT[7，8]和 NT[9]算法。

研究基于已有的CT動態圖軟件水印算法，提出一種新的基于PPCT(Planted Plane Cubic Tree)、排序圖和中國剩余定理的水印算法DGSW算法。實驗仿真表明，使用DGSW水印算法方案的CT軟件水印算法在抗攻擊能力方面有所提高，同時具有較好的數據嵌入率。

1 動態圖軟件水印技術

動態軟件水印系統評估性能的方式有別于靜態軟件水印系統。動態水印算法在嵌入水印時要考慮靜態數據嵌入率和動態數據嵌入率兩種嵌入率。靜態數據嵌入率是指在程序中嵌入多少生成水印的額外代碼，而動態數據嵌入率是指在程序運行時生成多少額外的數據。此外，動態軟件水印算法的隱蔽性分為靜態隱蔽性和動態隱蔽性兩種。靜態隱蔽性是指生成水印的代碼的存在是否容易被感知或定位的能力，而如果程序運行時生成的有關水印的數據結構能夠與程序原本的數據結構協調一致，那么就說算法是動態隱蔽的。

CT算法需要將水印數字轉換成對應的生成圖結構的代碼，圖的結構對水印嵌入率和隱蔽性具有非常重要影響。不同的圖編碼方案如底數圖、排序圖等等，單位比特的水印對應的圖的大小是不一樣的，因此影響了生成水印的代碼的體積。而數據嵌入率越低，圖對應的水印代碼的量越大，水印隱蔽性就越差。所以，文中致力于研究改進CT算法的圖編碼方案，從而提高算法的數據嵌入率和隱蔽性。

CT動態水印算法的抗干擾能力是一項重要指標，主要取決于算法采用的圖編碼方式。例如，排序圖不能抵抗邊翻轉攻擊，如果攻擊者交換其中幾條邊的順序，那么圖的結構就會完全發生改變，對應的水印數字就不一樣了。提出一種新的編碼方案DGSW，其抗攻擊能力更強，即使圖的結構由于攻擊被改變，仍然可以發現并糾正錯誤，從而還原出正確的水印，同時也能夠保持較高的數據嵌入率。

2 DGSW算法

2.1 嵌入過程

DGSW使用中國剩余定理，首先構造一個同余方程組把一個水印W分解成一個余數的集合，這些余數代表W的各個片段，只要獲得足夠多的片段就能恢復出W。算法如下:

(1)選取r個兩兩互素的數 p1，p2，…，pr，使 W＜∏rk=1pk。

(2)把W分解成r(r－1)/2個形如W'≡xkmodpikpjk(0≤xk＜pikpjk)的整數。

(3)利用中國剩余定理解出W。

這其中最關鍵的是，不需要將所有的同余方程都找齊才能夠得到最終的水印數字。只要把模數的因子p1、p2、…、pr找全，就能夠還原出正確的水印。換句話說，在運氣最好的情況下，只需要找到[r/2]個水印片段就能夠正確恢復水印。所以在這個例子中，即使這3個片段丟失或者被篡改任意1個，依然有機會計算出正確的水印數字。

通過上述算法獲得水印W的各個片段后，需要構造每個水印片段對應的子圖并將它們連接。設子圖中葉子結點的個數為n，要選取足夠大的n使n個結點形成的排序圖所表示的數的范圍大于子圖對應的同余方程的模數，并且葉子結點數為n的PPCT結構所表示的整數范圍同樣足夠大能表示余數。這里采用的選取方法是，根據PPCT結構的特點，計算出最小n，使Calalan(n)＞=余數，再計算出最小的n'，使n'!＞=橫數。最后選出max(n'，n)，作為最終的子圖的葉子結點個數，從而構造出對應的圖結構。首先構造以下同余方程:

其中0＜k≤r(r－1)/2。

利用如下算法可以構造出完整的圖結構:

for(each subgraph k)

calculate n1Catalan(n1)≥Wkand n1is minimum

calculate n2PermutaitonGraphLength(n1)≥pikpjkand n2is minimum

n=max(n1，n2)

build PPCT structure according to n and Wk

build Permutaiton Graph

connect each subgraph

下面用一個示例來具體說明嵌入過程。假設要將水印W=25分解成3部分。

(1)首先選取3個兩兩互質的數，這里選取p1=2、p2=3、p3=5 這3 個數。

(2)接下來把25分解成一個含有3個方程的同余方程組:

由此計算出1和5、10是水印數字25的3個分解片段。然后根據這3個片段及其對應的模數構造相應的子圖，最后連接這3個子圖就完成了水印的嵌入過程。同理，在提取水印時，根據圖的結構還原同余方程組，再根據中國剩余定理計算出水印。

該同余方程組對應的圖結構如下圖1所示。

圖1 同余方程組結構

余數1對應的PPCT圖的葉子結點個數為1，而模數6對應的排序圖的結點個數為3，所以選取3作為葉子結點個數構造對應的PPCT結構，再根據排序圖編碼方案改變葉子結點右指針方向使其表示模數6.依此類推，構造出其他的2個子圖。最后把這些子圖通過他們的生成結點相連形成一個完整的圖結構。

圖中箭頭都表示圖的邊，但是作用不同。箭頭3用于分割子圖，箭頭1用于連接子圖內PPCT結構的結點。箭頭2表示模數。在每個子圖內部，各個葉子結點的右指針(箭頭2)以排序圖的方式編碼，用于表示該子圖對應的同余方程的模數，而子圖的PPCT結構對應這個同余方程的余數。如最左邊的子圖對應的PPCT結構表示1，而葉子結點形成的排序圖表示6。

2.2 提取過程

首先把表示同余方程組的完整圖結構分割成若干子圖，分析每個子圖的PPCT是否完整，然后對每個子圖進行解碼得到對應的同余方程，進而還原出同余方程組。由于水印可能受到攻擊，所以接下來要過濾掉錯誤的水印片段從而得到正確的同余方程組。辦法是首先建立兩個圖G、H，每一個方程在G、H中都有對應的頂點，并計算出各個子圖對應的同余方程，如果兩個同余方程不相容(不相容有2種情況，第一種情況指2個方程模數相同但是余數不同，另一種情況是指2個方程的模數中有一個因數相同，但是方程的余數模這個因數得到的余數不同)，就在G的對應結點之間建立一條邊，如果兩個方程相容，就在圖H的對應結點之間建立一條邊。從圖H中找出最大的頂點，因為和這個方程相容的其他同余方程最多，所以這個方程是正確的。接下來將這個頂點對應的方程放到同余方程組U中，并將這個頂點和與它不相容的頂點從H、G中刪除，不斷重復這個過程直到圖G變成一個空圖為止。最后應用中國剩余定理就能夠計算出同余方程組U表示的水印了。

下面用一個示例具體說明過濾錯誤片段的過程。已知從各個子圖提取出以下同余方程組:

其中 p1=2、p2=3、p3=5。

前3個方程是原來正確的方程，而第4個方程是與原水印不相干的方程。

在圖G、H中各構造這4個方程對應的頂點。由于第1個方程與第3個方程不相容，圖G中這2組頂點間就有了一條邊。只要不斷在G中去掉頂點和對應的邊，最后就能夠去掉第4個方程得到如下同余方程組:

然后拆解同余方程組得到以下方程:

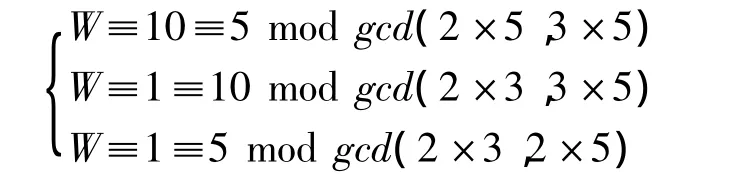
最后利用中國剩余定理解出這個同余方程的解W。

由該方程組可知其中存在很多冗余方程，因此只要把模數的因子p1、p2、…、pr找全，就能夠得到還原出正確的水印。在運氣最好的情況下，只需要找到[r/2]個水印片段就能夠正確恢復水印。所以在這個例子中，即使這3個片段丟失或者被篡改任意一個，依然有能計算出正確的水印數字。

3 仿真測試

3.1 數據嵌入率

圖2 3種編碼方案的水印嵌入率

計算DGSW理論上的數據嵌入率不僅比較困難，而且計算結果與實際不太一致，因為CT軟件水印算法真正需要的是產生水印圖所需代碼盡可能地少，而水印圖所表示的數盡可能大的一種圖，所以通過實驗測量單位比特水印對應的圖的代碼體積是最佳選擇。圖2顯示3種編碼方案的水印嵌入率，由圖2可知，提出的新編碼方案數據嵌入率優于PPCT編碼，與排序圖相差無幾。

3.2 抗干擾能力

3.2.1 抵抗邊翻轉攻擊

該水印算法采用了PPCT結構，因此具有很好抵抗邊翻轉攻擊能力。雖然在新編碼方案中葉子結點構成的排序圖無法抵御邊翻轉攻擊，排序圖所表示的模數會因此改變。根據中國剩余定理，提取水印時只要能夠找齊各個模數的因子，就能夠正確提取水印，改變少數幾個模數的大小并不會影響正確的提取因子。再加上可以在同余方程組中添加冗余方程增強糾錯能力，因此，新的編碼方案相較于已有的PPCT和排序圖的抵抗邊翻轉攻擊的能力都要強。

3.2.2 抵抗結點分裂攻擊

結點分裂攻擊指把動態分配的內存對象一分為二，變成2個不同的對象，并且讓第一個對象指向第二個對象。為了抵抗這種攻擊，該編碼方案可以轉換成一個m次的循環結構，并將所有的邊都換成一個m次的鏈接結構。任何的結點分裂都會融入循環結構或者鏈接結構當中，提取水印時需要規約這些循環和鏈接結構，還原出原來的水印圖，因此能夠自然消除結點分裂帶來的影響，如圖3所示。

圖3 DGSW水印方案抵抗節點分裂攻擊

最上面的是一個表示整數3的底數圖，在經過循環處理后變成了下面所示的結構。結點1、2、3都變成了3個結點的鏈接結構，A、B、C 3條邊也是如此。即使這樣的結構遭受結點分裂攻擊，在最后還原水印圖時攻擊產生的影響都能夠被消除。

3.3 隱蔽性

由于對具有海量且復雜鏈接的數據結構的程序進行別名分析是非常困難的，所以CT算法具有很好的動態隱蔽性。然而CT算法本身并不能保證水印的靜態隱蔽性，所以必須使用代碼混淆等保護技術使得程序源代碼可分析性降低。因此需要通過實驗判斷現有的代碼混淆技術是否會對CT算法的水印的提取產生影響。

以下測試的是本編碼方案抵抗代碼混淆處理的能力。其中“+”表示能夠抵御混淆處理，水印能夠正常提取，”－“表示不能抵御混淆處理。修改比例指程序中混淆的方法數占總方法數的比例。

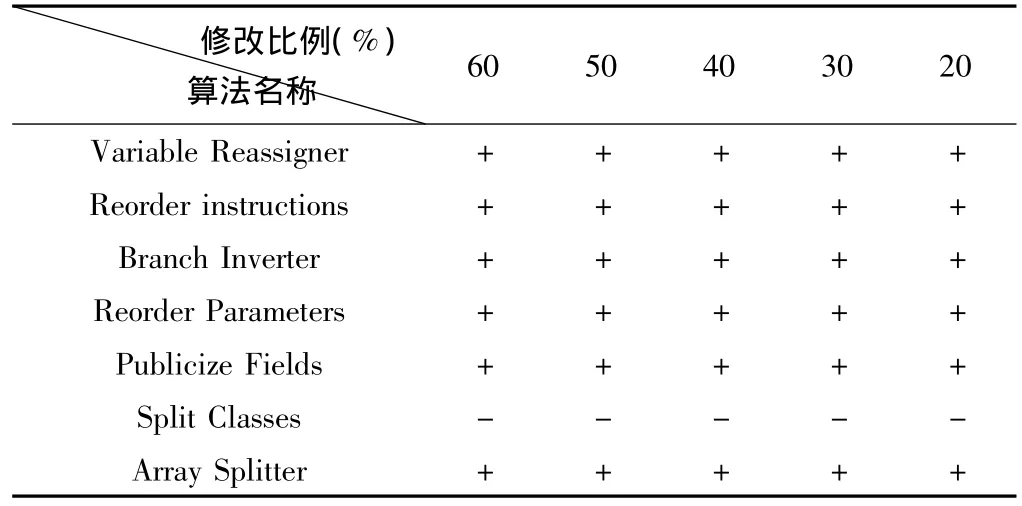
表1 代碼混淆技術對水印提取的影響

由表1可知，除了Split Classes這個混淆算法之外，其余的混淆算法對水印的提取沒有任何影響。

4 結束語

在CT算法的現有編碼方案基礎上，綜合中國剩余定理和現有編碼方案的一些優點提出DGSW編碼方案。實驗結果表明這套編碼方案具備抗攻擊能力強，糾錯能力好，數據嵌入率較高的優勢。

[1] Davidson R I，Myhrvold N.Method and system for generating and auditing a signature for a computer program:US，US5559884 A[P].1994.

[2] Hattanda K.The evaluation of Davidson＇s digital signature scheme[J].Ieice Transactions on Fundamentals of Electronics Communications＆Computer，2004，87(87-A):224－225.

[3] Myles G，Collberg C，Heidepriem Z，et al.The evaluation of two software watermarking algorithms.[J].Software Practice ＆ Experience，2005，35(10):923－938.

[4] Myles G，Collberg C，Heidepriem Z，et al.The evaluation of two software watermarking algorithms[J].Software Practice ＆ Experience，2005，35(10):923－938.

[5] Moskowitz，Scott A，Cooperman Marc.Method for stega-cipher protection of computer code[M].U-nited States Patent 5745569，1996.

[6] Collberg C，Thomborson C.Software watermarking:Models and dynamic embeddings[C].In:Principles of Programming Languages 1999，POPL 1999.

[7] Collberg C S，Thomborson C，Townsend G M.Dynamic graph-based software fingerprinting[J].Acm Transactions on Programming Languages＆Systems，2007，29(6):695－706.

[8] Palsberg J，Krishnaswamy S，Kwon M，et al.Experience with software watermarking[C].Proceedings of Acsac Annual Computer Security Applications Conference，IEEE Computer Society，2000:308.

[9] Nagra J，Thomborson C.Threading Software Watermarks[J].Lecture Notes in Computer Science，2004:208－233.

[10] Collberg C S，Thomborson C.Watermarking，Tamper-Proofing，and Obfuscation-Tools for Software Protection[J].Software Engineering IEEE Transactions on，2002，28(8):735－746.

[11] Christian Collberg，Jasvir Nagra.軟件加密與解密[M].北京:人民郵電出版社，2012:432－443.