運用同倫攝動法結合參數展開法求解強非線性問題

閆曉芳，陳 頌

(永城職業學院基礎部，河南永城476600)

當前，同倫理論已經成為研究不含有小參數的強非線性系統解的一種有效的解析方法，何吉歡結合同倫理論和攝動法提出了同倫攝動法(HPM).最近又發展了一系列新的攝動理論，并得到了進一步的發展，如人工參數法、參化攝動方法、改進的Lindsted－Poincare法的參數展開法等.這些方法都不將方程中的參數作為攝動參數，而是通過一定的方法(如人為地引進一個攝動參數，同倫技術，線性變換).而對于一些方程，傳統的攝動理論已不再適用，因此本文主要將同倫攝動法(HPM)和改進的 Lindsted－Poincare 法［1，2］的參數展開法有效結合，求解一些強非線性振動問題的近似解，所得結果與精確解比較，來驗證方法的有效性.

1 同倫攝動法結合參數展開法概述

考慮如下一般方程［3］

式中β，ε為參數且有0≤ε＜∞對此類方程我們還可以有如下解法:

首先，構造同倫如下:

其中p為小參數.其次方程的解u及參數β分別可以展開成p的冪級數，

將式(3)、(4)分別代入方程(2)，并比較等式兩端p的同次冪可得到兩個二階線性微分方程，從而易求出其解.

2 方法運用

運用同倫法結合參數展開法求解如下方程

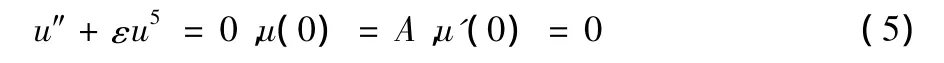
其中0＜ε＜∞.同倫攝動法已經解決不了上述方程，把方程(5)構造同倫重新寫成如下形式

其中p∈(0，1).當p=0時，方程(6)變為一線性方程，當p=1時，方程(6)變為原方程(1).

其次將方程的解u及參數0展開如下:

將式(7)，(8)代入式(6)并比較等式兩端p的同次冪系數可得

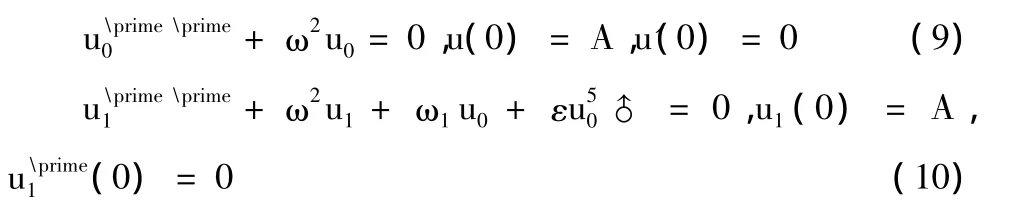
解方程(9)我們可以得到

將其代入式(10)得到

消除長期項……