n階非齊次線性微分方程通解結(jié)構(gòu)的判定

段素芳

(青島理工大學(xué)琴島學(xué)院，山東青島266106)

目前關(guān)于求非齊次線性微分方程的通解，主要是求一、二階非齊次線性微分方程的通解(或特解)［1］，還有的求三階(常系數(shù))非齊次線性微分方程的通解［2］，本文推廣以后得到n階非齊次線性微分方程通解的結(jié)構(gòu)與一、二階方程通解的結(jié)構(gòu)相同.

1 一階非齊次線性微分方程通解的結(jié)構(gòu)

首先，利用分離變量再積分的方法得齊次方程(2)的通解為 y=ce-∫p(x)dx，c為任意常數(shù).

其次，利用常數(shù)變易法得非齊次方程(1)的通解

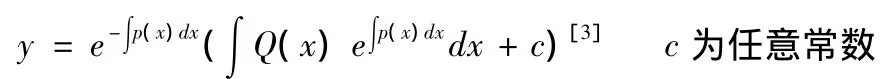
而方程(2)的通解為Y(x)=ce-∫p(x)dx

故一階非齊次線性微分方程通解的結(jié)構(gòu)為

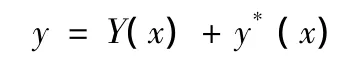
2 二階非齊次線性微分方程通解的結(jié)構(gòu)

關(guān)于二階非齊次線性微分方程的通解有如下定理

定理［3］設(shè)y*(x)是二階非齊次線性微分方程(3)的特解，Y(x)是對應(yīng)齊次方程(4)的通解，則y=Y(x)+y*(x)是方程(3)的通解.

注:以上定理對二階常系數(shù)非齊次線性微分方程同樣成立.

3 定理及證明

由一、二階常系數(shù)非齊次線性微分方程通解的結(jié)構(gòu)推廣到n階常系數(shù)非齊次線性微分方程，得如下結(jié)論

定理n階常系數(shù)非齊次線性微分方程為

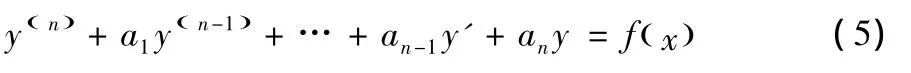
設(shè)Y(x)是n階常系數(shù)齊次線性微分方程

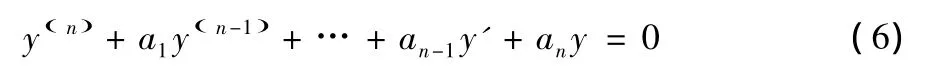
的通解，y*(x)是方程(6)的特解，則n階常系數(shù)非齊次線性微分方程(5)的通解為

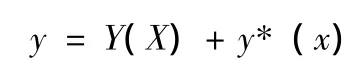
其中方程(6)的通解為Y(x)=c1y1+c2y2+…+cnyn，y1，y2，…yn是方程(6)的n個線性無關(guān)的特解.

證明:設(shè)y* 是方程(5)的特解，y1，y2，…yn是對應(yīng)齊次方程(6)的n個線性無關(guān)的特解，則齊次方程(6)的通解為Y(x)=c1y1+c2y2+…+cnyn

又設(shè)方程(5)的任意一個解為y，則y-y* 是對應(yīng)齊次方程(6)的一個解，

于是存在不全為零的n個數(shù)c1，c2，…，cn使得y-y* =c1y1+c2y2+…+cnyn

即y=y* +c1y1+c2y2+…+cnyn

上式即為n階常系數(shù)非……