基于PBL的離散數學課程教學創新實踐

李 俊 諸葛霞 廖遠江

（寧波工程學院電子與信息工程學院，浙江 寧波315016）

0 引言

“離散數學”課程是研究離散量的結構和相互間關系的一門學科，它充分描述了計算機科學離散性的特點，是計算機科學技術及相關專業的核心課程，可以為計算機科學技術及相關專業的學生提供重要的理論基礎，例如程序設計語言、數據結構、數據庫技術、算法分析、可計算性與計算復雜性理論、邏輯設計、系統結構、容錯診斷、人工智能與機器定理證明等課程[1-2]。

為了能激發學生學習的積極性，達到最佳的教學目的,本文通過調研和結合近年來的教學實際情況，從教學方法和手段等方面進行探索,提出了基于PBL教學模式的“離散數學”課程教學創新實踐。

1 “離散數學”教學現狀分析

“離散數學”是計算機科學技術及相關專業的骨干課程[3]，與其他計算機課程相比有相似的方面，但也有其獨特的地方，分析“離散數學”課程的特點，以及在教學實踐中常存在的問題主要體現在以下幾個方面：

（1）離散數學定義多、定理多，內容抽象，邏輯性強,大多數教師只重視理論知識的教授，忽略了實踐環節，使學生誤認為離散數學是一門理論課，對本專業的實際應用作用不大,因此不重視學習，甚至出現厭學心理。

（2）離散數學課程中的定義和定理難理解難記憶，公式和證明也特別多，有些學生掌握了基礎知識，也背會了定義、定理和公式，但不會做題，所以很多學生認為離散數學是一門難學的課程，甚至有些學生認為離散數學是計算機專業中最難學的課程。

（3）離散數學內容豐富，包含數理邏輯、集合論、代數系統、圖論、組合數學等多個知識點。大多數教師能認真深入地講好每個知識點,但是很少老師會把這些知識點之間的聯系介紹出來，所以使大部分學生誤認為離散數學課程是由幾個相互獨立的知識點組成，各知識點之間聯系少，缺少體系完整性，導致學生對課程內容理解的不深入和透徹，達不到學習目的。

（4）離散數學內容多，課時少，一般高校在教學培養計劃中將該課程設置為64學時，甚至有的學校設置成54學時[4]，在這些學時中教師只能主要以追求講授理論知識為主，缺少理論聯系實際的實踐教學環節，導致學生不知道到如何使用這門學科為計算機科學的應用和發展提供有效地服務。

針對“離散數學”課程的特點，以及在教學實踐中存在的這些問題，本文提出一種基于PBL的教學模式用于“離散數學”課程的教學研究，通過以問題為導向，倡導以學生主動學習為主的教育方式使學生認識到學習離散數學對計算機專業的重要性，以及激發學生學習的積極和主動性。

2 基于PBL離散數學教學方法

離散數學是計算機專業的一門核心課程，為了提高教學質量，達到教學目的，以及理論知識與實踐技能協同發展和互相促進，本文提出了一種基于PBL教學模式的“離散數學”教學研究。其教學模式是：

（1）上課前，為了使學生對教學新內容產生濃厚的興趣和強烈的求知欲，提高學習效率和課堂的教學質量，教師針對學生的專業知識特點及授課任務，設計可行有效的教學方案，并結合授課內容提出和專業知識相關的一道或若干道問題,以問題為導向要求學生圍繞所提問題充分預習教材、查找相關資料、課下分組探討解決方案。例如在講圖論中的最短路徑知識時可以向學生提出下面的從一個城市到另一個城市的最短路徑問題，使學生圍繞該問題預習和探討授課新內容。

所提問題：圖1為7個城市A，B，C，D，E，F，G之間的一個公路圖，該圖用G表示，結點（用V表示）代表城市，邊（用E表示）代表城市之間的公路，邊上的權值（用W表示）表示該段公路的長度。考慮編寫一個程序的算法，該算法能夠自動算出從一個城市到另一個城市的最短路徑及距離。

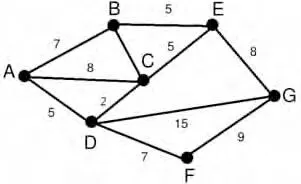
圖1 城市公路圖

（2）課堂內，教師首先鼓勵學生積極發言，讓學生以解決問題為支架陳述其自學方法、自學過程、自學內容，以及解決問題的方；然后教師講授教學內容，講解應用教學新內容對所提出問題的解決方案；最后教師對學生所提出問題的解決方案給予評價，對其有解決方法較好和具有創新想法的同學給予贊賞，對解決方法不足之處給予補充，以有效地培養和訓練學生自主學習，分析問題，解決問題和創造思維能力。例如上面求最短路徑問題，我們首先講解最短路徑知識，然后利用該知識給出下面的從一個城市到另一個城市的最短路徑及距離的解決方案，再對學生所提出問題的解決方案給予評價。

從一個城市到另一個城市的最短路徑及距離的解決方案：給出一個城市到其余城市的最短路徑及距離算法，其它城市之間的最短路徑及距離可以類似解出[5]。下面以圖1中的A城市為例，介紹一個城市到其余城市的最短路徑及距離算法求解的主要步驟：

（1)把圖1中城市集合V分成兩組：第一組為已求出最短路徑的城市集合(用S表示)，第二組為其余未確定最短路徑的城市集合(用U表示)。初始時,S只包含城市A，即S={A}，A到A的距離為0。U包含除A外的其他城市，即U={B,C,D,E,F,G}，U中各城市到城市A的距離為邊上的權值(若兩城市之間有公路)或∞(若兩頂點之間無公路)。

（2)把k加入S中(該選定的距離就是城市A到城市k的最短路徑長度)。

（3)以k為新考慮的中間點,修改U中各城市的距離：若從城市A到城市u(u∈U)的距離(經過城市k)比原來距離(不經過城市k)短,則修改城市u的距離值,修改后的距離值的城市k的距離加上邊fflt;k,u＞上的權。

（4)重復步驟（b)和(c)直到所有城市都包含在S中。

(3)課堂后，讓學生上機實驗，把問題程序化，以幫助學生加深對所學知識的理解與消化，同時也鍛煉學生編程能力和應用離散數學的理論知識解決計算機專業實際問題的能力。

3 結束語

針對“離散數學”課程特點，本文通過調研和結合近年來的教學實際情況，從教學方法和手段等方面進行探索，提出了一種基于PBL教學模式的“離散數學”課程教學創新實踐，即教師課前提出問題——學生查找資料、分組討論——教師教授新內容和給出問題的解決方案——學生上機實踐。該模式即能給學生提供有針對性的思維支架，激發學生學習的積極性，又有助于教師從多方面考慮PBL理念的方法在教學中的應用，提升教學設計的有效性，達到教與學的目標。

［1］屈婉玲.離散數學[M].高等教育出版社,2008.

［2］文海英,廖瑞華,魏大寬.離散數學課程教學改革探索與實踐[J].計算機教育,2010,(6)：100-103.

［3］張蕾,黃文芝.“離散結構”課程的教學探索[J].中國電力教育,2011(17)：96-101.

［4］譚作文.離散數學課程中實驗教學探討[J].計算機教育,2010(6)：106-109.

［5］李春葆,尹為民,等.數據結構教程[M].清華大學出版社,2009.