大型航天器桁架式主承力結構構型拓撲優化研究

（中國空間技術研究院，北京 100094）

1 引言

以桁架作為主承力結構的大型航天器，如大型桁架式衛星等，其構型設計所受的約束條件頗多，運載火箭、推進方案、熱控方案和有效載荷類型等對構型設計均有不同程度的影響。此外，還要考慮傳力、平臺設備之間的電連接、傳熱，以及裝配和維護等要求。在構型設計初期，首先是滿足傳力要求。合理的傳力路徑能用較少的結構材料獲得較高的結構剛度和強度。

隨著航天技術的發展，滿足現代航天器日趨復雜的結構本身對結構性能越來越高的要求，必須應用結構優化設計技術［1］。國外某些航空航天公司已將結構優化作為結構設計中的規范環節［2］；在國內，優化設計方法也開始在航天器結構設計中得到初步應用［3-4］。現階段，結構參數優化的應用研究較多，而結構拓撲優化的應用研究相對較少。

本文以大型航天器平臺桁架式承力結構的研發為背景，在其概念設計階段，根據平臺設計要求和外部約束，應用連續體-離散體兩級拓撲優化策略得到了桁架式承力結構的構型形式，所得結果可為詳細設計階段提供依據。與尺寸優化和截面形狀優化相比，桁架結構構型拓撲優化能夠在更大范圍內改善結構特性，進而使所得承力結構質量更小，性能更優。本文提出的優化策略也可用于其他桁架式承力結構的設計工作。

2 連續體-離散體兩級拓撲優化策略

桁架式結構強度高，通用性、組合性好，形式簡單，傳力路線合理，易于實現模塊化且可擴展，因此特別適于用作某些大型航天器的主承力結構。桁架結構能夠傳遞集中載荷，沿著載荷的主要傳力路徑布置桿件，能夠顯著減小結構質量，提高結構性能。

結構拓撲優化是一種尋找結構傳力路徑的有效方法。根據優化對象的結構類型的不同，結構拓撲優化可分為連續體結構拓撲優化和離散體結構拓撲優化，在此前的研究工作中，兩者一般不同時應用。前者用于從二維或三維設計區域中去除低效能材料，得到的剩余材料的分布情況可指導詳細設計［5］；后者多采用基結構法，優化過程從大量初始桿件（即基結構）中刪除低效能桿件，得到所需的桁架結構，但其最初基結構的主要節點和桿件連接關系則是人為給定的。

為將連續體結構拓撲優化和離散體結構拓撲優化結合起來進行桁架結構的設計，提出連續體-離散體兩級拓撲優化策略（見圖1）。首先，進行連續體結構拓撲優化。根據桁架結構總體設計要求，給出連續體結構拓撲優化的可行設計區域，并設定目標函數和約束條件，形成優化問題。利用工具軟件（如HyperWorks／OptiStruct）求解計算可得到類似桁架結構的優化結果，在此基礎上進行歸納提煉，得到由桿件組成的標準桁架結構形式。然后，進行離散體結構拓撲優化。以連續體結構拓撲優化得到的桁架結構為基礎，根據經驗人為地添加節點和桿件，增加其他可能的傳力路徑，得到其拓展基結構，再按照離散體結構拓撲優化數學模型進行優化，即可得到最終的桁架式結構構型。如有多個方案，還可對比選優。

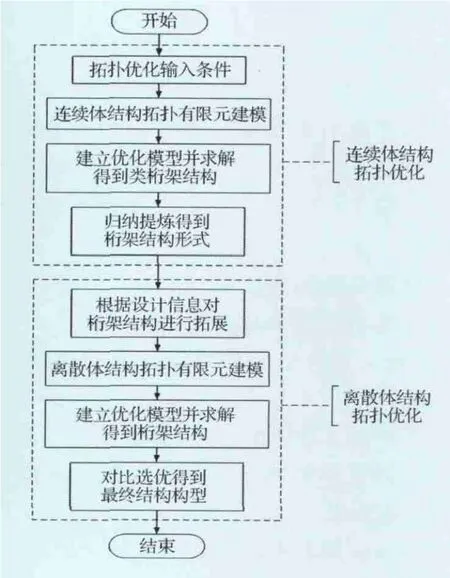
圖1 桁架結構優化設計流程Fig.1 Flow chart of optimal design for truss structure

3 大型航天器桁架式承力結構拓撲優化

3.1 問題描述

設定大型航天器采用模塊化設計，其主體結構由載荷艙和平臺兩部分組成，其中平臺部分采用桁架式的主承力結構，用于連接平臺底部航天器和火箭的對接環和頂部載荷艙，見圖2。以對接環底面圓心為坐標原點，各坐標軸方向如圖2所示。

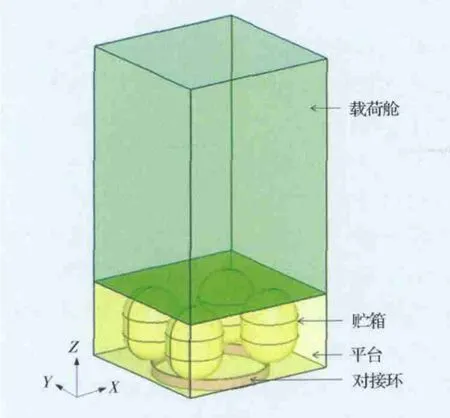
圖2 航天器主體結構示意圖Fig.2 Sketch map for main body of spacecraft

航天器的總質量為7000kg時，其剛度滿足一階橫向頻率不小于8 Hz、一階縱向頻率不小于30Hz的要求；航天器平臺應滿足所采用運載火箭整流罩的包絡要求；載荷艙要求平臺頂端應有不少于5個的傳力點；在保持航天器結構構型不變的前提下，結構平臺的承載能力可擴展；航天器和火箭的對接環直徑不小于2000 mm。在上述要求的約束下，對航天器平臺部分桁架式承力結構的構型形式進行設計。

3.2 連續體結構拓撲優化

3.2.1 邊界條件和載荷條件

受運載火箭包絡尺寸的限制，并考慮平臺安裝太陽翼、天線等設備和散熱的要求，平臺基本尺寸確定為2880mm×2880mm。推進劑貯箱直接安裝在對接環上，四貯箱并聯安裝。根據推進劑預算可確定單個貯箱容積，設計為直徑大于1000 mm、高度大于1300mm 的球頭貯箱。對接環直徑按要求暫取為2000mm。

根據運載方規定的航天器設計載荷條件，并考慮1.25的安全系數，確定平臺結構X和Y兩個橫向加速度載荷為3gn，縱向（Z向）加速度載荷為8gn。

需要說明的是，除幾何包絡要求、邊界約束條件、載荷加載形式和初步確定的承力點位置外，連續體結構拓撲優化結果對設計區域結構的材料特性、集中質量點質量的絕對大小以及載荷的絕對數值都是不敏感的。不過，各方向載荷的相對大小變化時，其合矢量方向也會變化，對優化結果會產生一定的影響。

3.2.2 優化方法及優化問題數學模型

連續體結構拓撲優化應用HyperWorks軟件，采用變密度法進行優化［6］，應用的是固體各向同性懲罰微結構模型（Solid Isotropic Microstructures with Penalization，SIMP）［7］。該材料模型將結構設計域離散為n個有限單元，每個單元的彈性模量與其相對密度的關系可表示為

式中：xi為單元i的相對密度；E0為實體材料的彈性模量；Ei為單元i材料的彈性模量；p表示懲罰因子，在OptiStruct軟件中，與p有關的優化參數DISCRETE取值為（p-1）［8］。

圖3給出了p取不同值時相對彈性模量（Ei／E0）與相對密度xi的關系曲線。

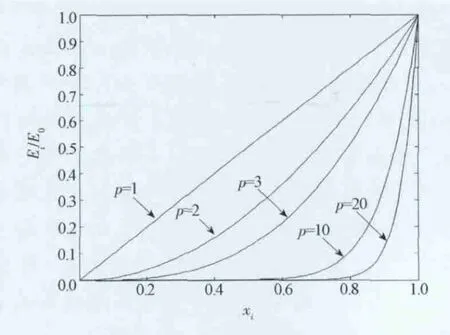
圖3 相對彈性模量與相對密度的關系Fig.3 Relative stiffness vs relative density

假定彈性體在受力作用的過程中始終保持平衡，因而沒有動能的改變，且彈性體的非機械能也沒有變化，于是，外力勢能的減少（也就是外力所做的功）就完全轉變為形變勢能（又稱為應變能）［9］。在這種情況下，外力功和應變能在數值上是一致的，可稱該值為靜態應變能，作為反映結構靜剛度的一個標量響應。那么，優化問題可描述為：受加速度載荷時，設計區域體積分數和航天器基頻約束下的結構靜態應變能最小，其設計變量為結構有限元模型中設計區域內每個單元的相對密度值。連續體結構拓撲優化問題的數學模型如下。

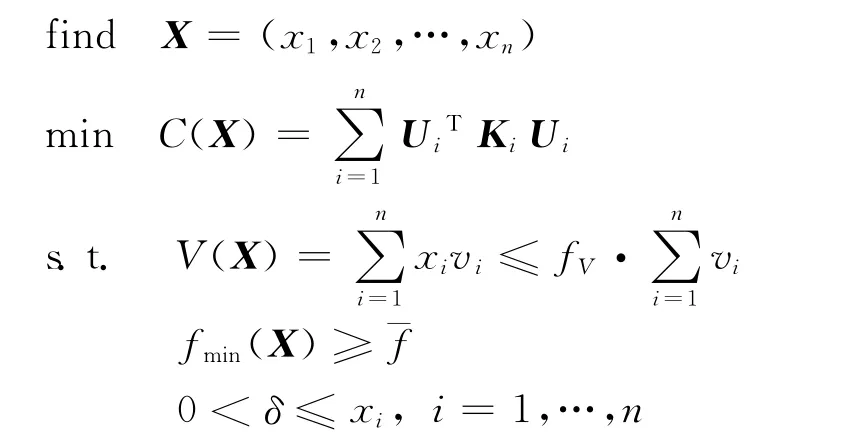
在該模型中，X＝（x1，x2，…，xn），為拓撲優化設計變量向量，xi為第i個單元的相對密度；C（X）為反映結構靜態應變能的量；Ui為單元i的位移向量；Ki為單元i的剛度矩陣；V（X）為設計區域結構總體積；fV為設計區域體積分數，vi為單元i的體積；fmin和分別為結構基頻及其下限；δ為一極小正數，用于避免剛度矩陣奇異。

3.2.3 結構有限元建模

根據已確定的邊界條件，平臺結構占據的幾何空間為一立方體，XY平面尺寸已知，高度則由貯箱高度確定。因為推進劑貯箱不能與其他結構發生干涉，所以立方體中還要預留出貯箱空間。氧化劑貯箱與燃料貯箱分別對角放置，使用梁單元模擬貯箱結構，單元自身的結構質量用來模擬未填充推進劑貯箱的結構質量，推進劑質量則通過非結構質量進行模擬。貯箱下端直接連接到對接環上，其上端則通過拉桿與平臺結構相連。平臺頂端的傳力點也是平臺結構的主要承載點，因此貯箱拉桿也是連接到這些傳力點上。有限元模型中使用集中質量點來模擬載荷艙的質量，考慮到設計要求中規定平臺頂端應有不少于5個的傳力點，提出五傳力點和七傳力點兩種質量分布方案。

基于以上考慮，本文構建了如圖4所示的有限元模型。其中：五傳力點模型共有43 193個節點，36 430個單元；七傳力點模型共有43 193個節點，36 434個單元。

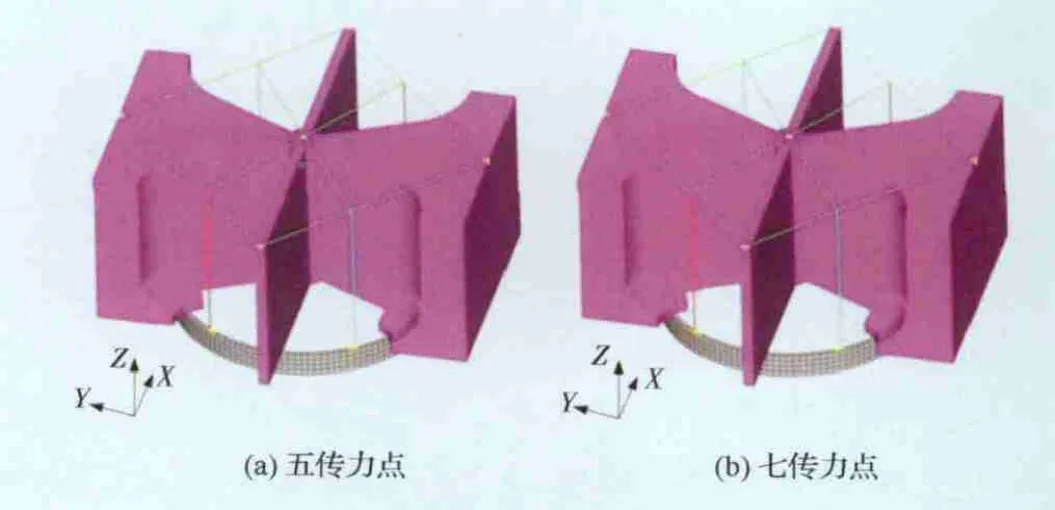
圖4 設計區域的結構有限元模型Fig.4 Finite element model for design domain

3.2.4 優化結果

基于已建立的有限元模型和優化的數學模型，通過不斷調整優化數學模型中的體積分數和結構基頻約束進行多次試算，并在已有優化結果上進行二次優化，最終得到五傳力點方案和七傳力點方案的連續體結構拓撲優化結果。兩個方案的優化結果傳力路徑清晰，易于提取出對應的桁架形式，可作為后續離散體結構拓撲優化的輸入條件。連續體結構拓撲優化結果及對應桁架形式如圖5和圖6所示。

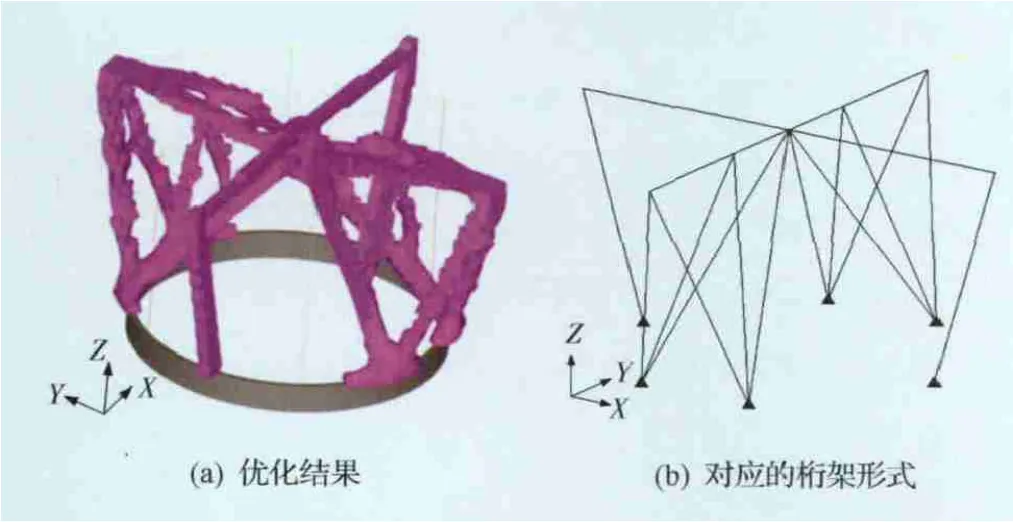
圖5 五傳力點方案連續體結構拓撲優化結果及對應的桁架形式Fig.5 Optimization result of continuum structure for fivejuncture scheme and its corresponding truss configuration

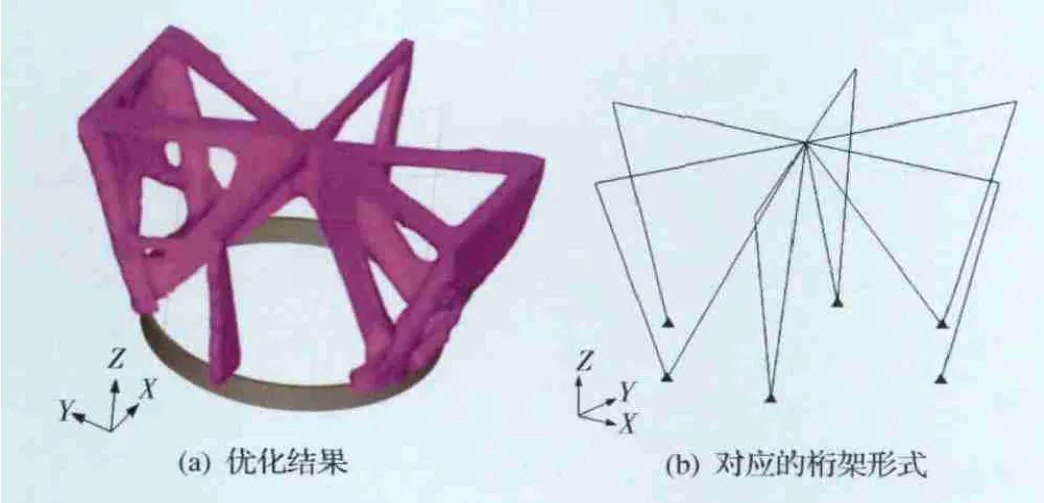
圖6 七傳力點方案連續體結構拓撲優化結果及其對應的桁架形式Fig.6 Optimization result of continuum structure for sevenjuncture scheme and its corresponding truss configuration

3.3 離散體結構拓撲優化

通過連續體拓撲優化，已經得到了桁架結構主要的節點信息和桿件分布形式，這時可對桁架結構進行進一步優化，增加必要的節點和桿件，再通過離散體結構拓撲優化設計使桁架結構的構型更加合理。

3.3.1 邊界條件和載荷條件

離散體結構拓撲優化時的邊界條件和載荷條件，與連續體結構拓撲優化時基本相同，只是設計空間由三維實體結構換成了空間桁架。

3.3.2 優化方法及優化問題數學模型

求解離散體結構拓撲優化問題時常用的是基結構法。在設計空間內人為地布置足夠多的節點，并將每一個節點與其他所有節點用桿件連接起來形成基結構。在此基礎上進行截面尺寸優化，并將截面過小的桿件刪除，從而實現結構的拓撲優化。這就是基結構法的基本思想。

離散體結構拓撲優化的設計變量為設計桿元的橫截面面積，非設計桿元在優化過程中截面尺寸保持不變。優化目標為過載工況下的結構靜態應變能最小；約束條件為優化后桿件總體積不超過給定值（一般設置為初始桿件總體積的1／3），結構一階頻率大于某給定值。離散體結構拓撲優化的數學模型如下。

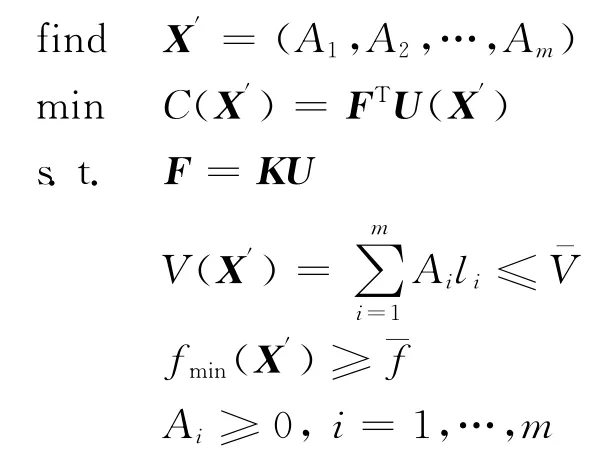
在該模型中，X′＝（A1，A2，…，Am），為拓撲優化設計中各桿件的橫截面面積，Ai為第i根桿的橫截面面積，m為桿件數；C（X′）為結構靜態應變能；F為節點等效載荷向量；U為節點位移向量；V（X′）為結構體積；li為第i根桿的長度；ˉV為體積約束上限；K為結構總剛度矩陣。

該模型所描述的優化問題中存在平衡方程約束，因此是一個非凸優化問題，難以找到全局最優解。為便于求解，可將優化模型進行轉化。應用半定規劃理論，通過一定的數學處理將該非凸模型轉化為凸性的半定規劃模型，即可通過內點法進行求解［10］。需要說明的是，模型中的平衡方程F＝KU必然滿足，但仍將其列出；靜態應變能在此處選用外力功的等價表達式，這樣的處理使得優化模型可以轉化為半定規劃的標準形式，便于求解。

3.3.3 基結構的拓展及有限元建模

在連續體結構拓撲優化得到的桁架結構基礎上進行拓展，增加必要的節點和桿件，添加可能的傳力路徑，形成桁架的拓展基結構，如圖7所示。使用桁架式結構拓撲設計優化系統（TOpology Design Optimization System of Structure with Truss，TODOSST）［11］進行離散體結構拓撲優化。與連續體結構拓撲優化相比，離散體結構拓撲優化有限元模型以桿結構為主，為各桿件賦予材料和尺寸信息；為貯箱設置適當的非結構質量來模擬推進劑質量；對結構相應節點施加固定支撐約束，并設置過載工況。各傳力點的集中質量可在TODOSST 的人機交互界面中添加。在界面中按照優化模型完成設置后，即可在MATLAB軟件環境中運行TODOSST，進行離散體結構拓撲優化。

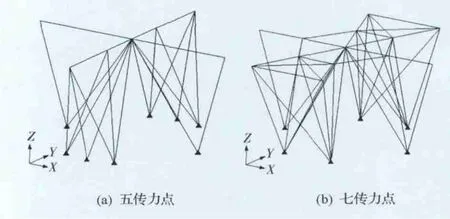
圖7 五傳力點和七傳力點方案桁架的拓展基結構Fig.7 Expanded base structures for both five-juncture and seven-juncture schemes

3.3.4 優化結果

以過載工況下的結構靜態應變能最小為優化目標，優化后桿件體積約束設置為結構初始總體積的1／3，并分別取不同的一階頻率約束，所得的優化結果分別如圖8和圖9所示。圖中均去除了截面積小于結構中最大桿件截面積1%的桿件；灰色部分為非設計桿元，黑色部分為設計桿元，桿件顯示的粗細僅表示其橫截面積的相對大小，不代表實際數值。

從圖8和圖9可見，對五傳力點方案，當一階頻率約束從12Hz開始不斷提高至22 Hz時，所得的離散體結構拓撲優化結果的拓撲形式是完全一致的，且當外圍桿件截面積增大時，結構基頻也相應提高。一階頻率約束大于24 Hz時，未能得到合理的優化結果。對于七傳力點方案，當一階頻率約束從10Hz開始不斷提高至24 Hz時，所得的離散體結構拓撲優化結果的拓撲形式是完全一致的。同樣的，當外圍桿件截面積增大時，結構基頻也相應提高，一階頻率約束大于27Hz時，未能得到合理的優化結果。

在以上優化結果中，刪除了某些次元（截面尺寸相對較小的桿件）之后，有可能產生機構，此時要人為合并相應節點以形成結構。圖10給出了以上離散體結構拓撲優化結果所得出的最優拓撲形式，其中七傳力點方案中暫時保留了外側小橫桿和“X”形交叉桿，可以認為它們模擬了外側箱板的支撐作用，不屬于桁架結構的組成部分。

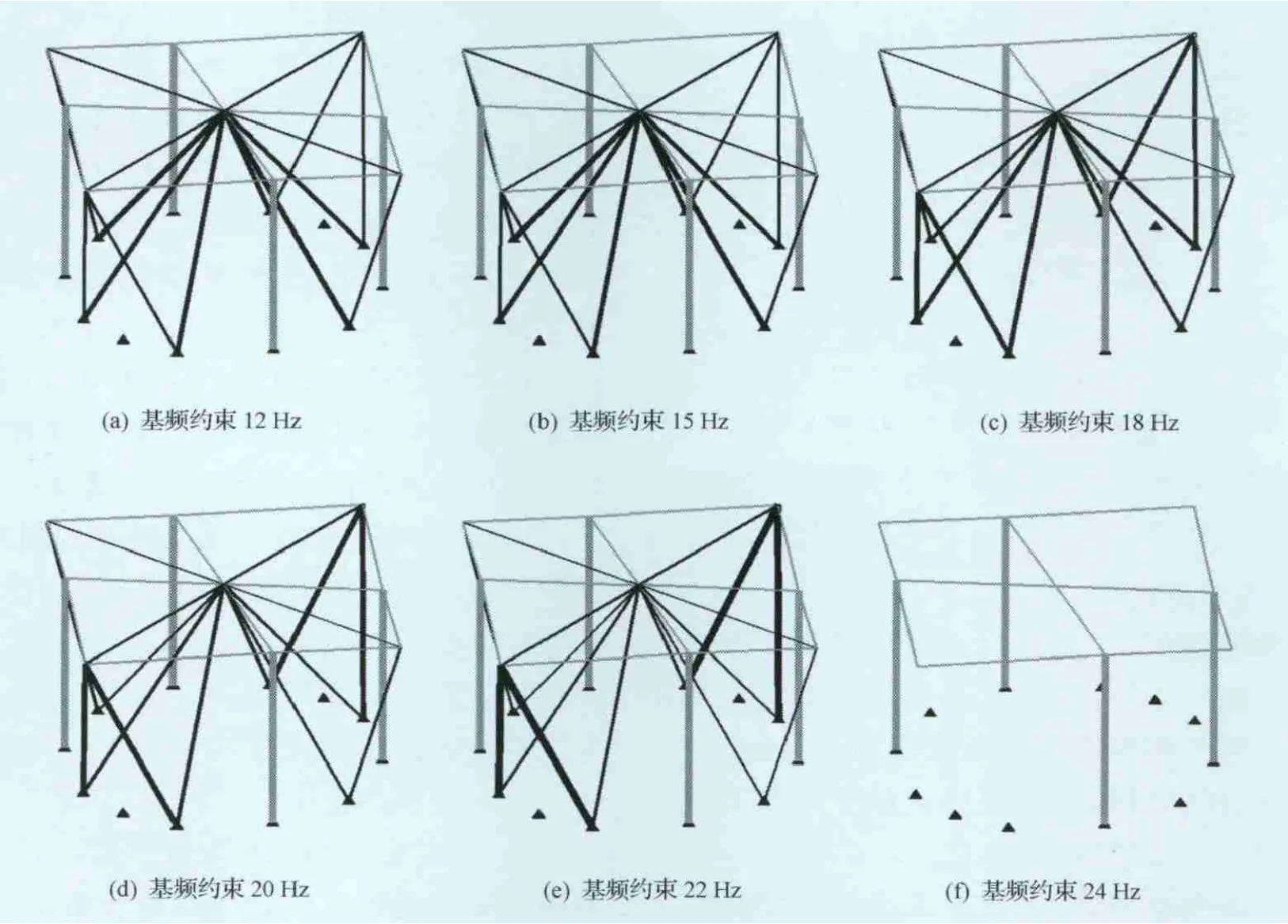
圖8 五傳力點方案中不同一階頻率約束時的離散體結構拓撲優化結果Fig.8 Topology optimization results of discrete structure for five-juncture scheme under various first frequency constraints

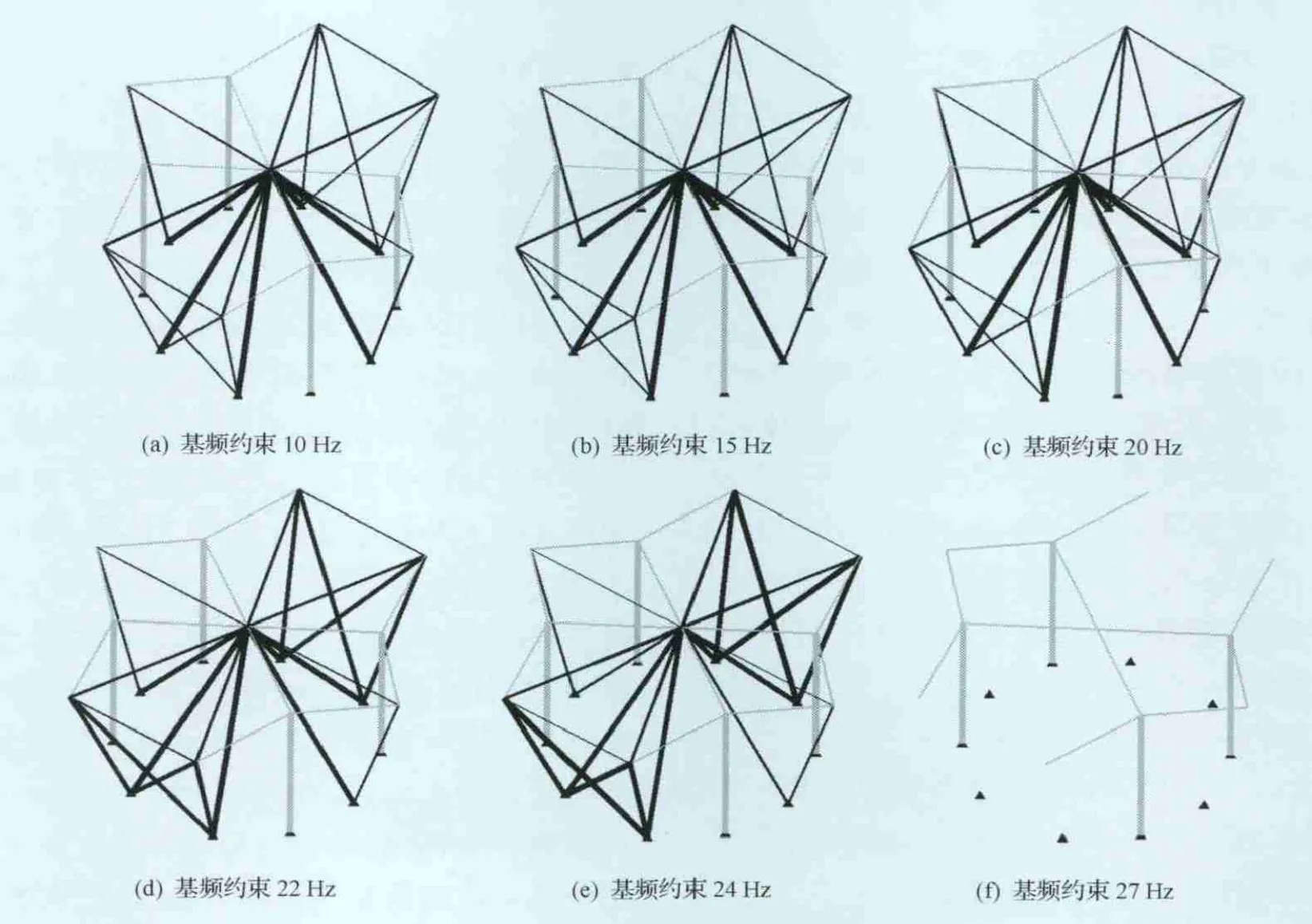
圖9 七傳力點方案中不同一階頻率約束時的離散體結構拓撲優化結果Fig.9 Topology optimization results of discrete structure for seven-juncture scheme under various first frequency constraints

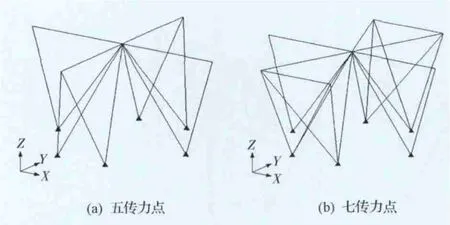
圖10 五傳力點和七傳力點方案經優化后的最終拓撲形式Fig.10 Final topology after optimization for both five-juncture and seven-juncture schemes

3.4 優化結構分析比較

兩種方案的優化設計結果均滿足設計要求中對于運載火箭包絡尺寸、對接環直徑和與載荷艙接口數量的要求。圖8和圖9的優化結果顯示，經過后期的詳細設計，所得的桁架構型形式能滿足航天器基頻要求，并具有一定的拓展能力。

對比圖8和圖9可發現，在不改變桁架結構構型的前提下，僅通過修改模型中各桿件的橫截面尺寸，七傳力點方案在給定的條件下能夠達到比五傳力點方案更高的結構基頻，因此具有更大的設計和優化空間。在最初確定貯箱分布方式時，有意將貯箱沿X方向的間隔拉大，以在中間位置預留更多的設備安裝空間。從五傳力點方案的優化結果可以看到，預留空間部分已被承力結構占據，該處可用空間被承力桿件分割得較為零碎，不利于設備的安裝；若考慮加裝隔板來增加結構的剛度和承載能力，由桿件的位置可以看出，隔板分布將會非常密集，且有多塊隔板為斜板（不與XOY平面垂直），即使結構剛度和承載能力有所提高，也會增加較多的結構質量，浪費更多的可用空間。另外，七傳力點方案中每個貯箱頂端的3個拉桿位置分布較均勻，拉桿長度也較為合理；五傳力點方案中拉桿分布相對來說不是很均勻，其中一根拉桿的長度明顯比七傳力點方案中的長，這樣既增加結構質量，又使傳力路徑變長，因而不是較為合理的設計方案。

根據以上幾點分析，七傳力點方案的優化結果具有比較明顯的優勢，建議以七傳力點方案的最優拓撲形式為基礎開展后續設計工作。

4 結構參數優化的討論

在結構拓撲優化設計階段，優化對象僅是桁架式主承力結構的構型形式，即主要節點的位置和節點間的桿件連接情況，后續工作中必須進行結構參數優化設計，其必要性主要體現在：

（1）從能量角度講，結構拓撲優化設計時的載荷艙結構僅由幾個集中質量點來模擬，未考慮實際載荷艙的彈性變形對基礎振動能量的吸收、儲存作用，也就是說，平臺桁架結構要自行吸收全部振動能量，設計偏保守。

（2）在實際發射過程中，一般不會出現3個方向同時受最大載荷的過載工況，進行結構拓撲優化設計時應用這種嚴酷的載荷條件也會使設計偏保守。

（3）結構拓撲優化結果對結構的材料特性、加速度載荷的絕對數值等都是不敏感的，設計要求中的某些技術指標在該階段起不到具體的約束作用。只有在航天器結構進行較細致建模時，航天器模型的力學特性才能達到與技術指標進行對比的程度，有必要進一步進行優化。

（4）經過初步的詳細設計，主承力結構中各桿件的橫截面形狀和材料特性均逐步明確，這時進行結構參數優化設計，能夠針對明確的設計變量進行優化，所得優化結果可直接用于指導結構設計，從而獲得更好的結構特性。

5 結束語

目前，連續體結構拓撲優化和離散體結構拓撲優化在航天器工程中的應用正在逐步普及，但大多只是單獨應用其中一類拓撲優化方法。本文提出針對桁架結構的連續體-離散體兩級拓撲優化策略，成功應用于大型航天器桁架式承力結構的優化設計，得到了基本滿足設計要求的桁架構型形式，可為后續詳細設計提供參考，同時也驗證了此種優化策略在解決特定的桁架結構優化設計問題時的有效性。結構優化方法雖然能夠指導結構設計，但在優化可行設計區域確定、連續體結構拓撲優化結果的提煉歸納、離散體結構桁架基結構的拓展等方面，工程經驗仍是必不可少的。拓撲優化設計僅僅是得到了桁架結構的構型形式，在此基礎上要進行進一步的結構參數優化，才能確定桁架中桿件的最優截面尺寸，達到減小結構質量、提高結構性能的目的。

（References）

［1］陳烈民.航天器結構與機構［M］.北京：中國科學技術出版社，2005：92-102 Chen Liemin.Spacecraft structure and mechanism［M］.Beijing：China Science and Technology Press，2005：92-102（in Chinese）

［2］澳汰爾工程軟件（上海）有限公司.澳汰爾優化設計在航空部件設計中的應用［J］.CAD／CAM 與制造業信息化，2004（9）：61-63 Altair Engineering Inc（Shanghai）.Application of Altair Optimization on aerial components［J］.CAD／CAM Yu Zhizao Xinxihua，2004（9）：61-63（in Chinese）

［3］周志成，曲廣吉，黃海.某衛星平臺多結構工況下的優化設計［J］.北京航空航天大學學報，2009，35（7）：821-823 Zhou Zhicheng，Qu Guangji，Huang Hai.Design optimization of satellite platform considering multiple structural cases［J］.Journal of Beijing University of Aeronautics and Astronautics，2009，35（7）：821-823（in Chinese）

［4］盛聰，曾福明，濮海玲.應用OptiStruct軟件的太陽翼基板結構優化［J］.航天器工程，2011，20（6）：63-68 Sheng Cong，Zeng Fuming，Pu Hailing.Optimization of solar panel structures by using OptiStruct［J］.Spacecraft Engineering，2011，20（6）：63-68（in Chinese）

［5］杜江華，陳昌亞，顧亦磊.拓撲優化方法在某衛星下艙隔板結構設計中的應用［C］／／第一屆結構及多學科優化工程應用與理論研討會論文集.北京：中國力學學會，2009：1-5 Du Jianghua，Chen Changya，Gu Yilei.Application of topology optimization method to optimal design of clapboard in a satellite lower-cabin［C］／／Proceedings of the 1st Structure and MDO Engineering Application and Theory Conference.Beijing：Chinese Society of Theoretical and Applied Mechanics，2009：1-5（in Chinese）

［6］張勝蘭，鄭冬黎，郝琪，等.基于HyperWorks的結構優化設計技術［M］.北京：機械工業出版社，2008 Zhang Shenglan，Zheng Dongli，Hao Qi，et al.Structural optimization technology based on HyperWorks［M］.Beijing：China Machine Press，2008（in Chinese）

［7］Eschenauer H A，Olhoff N.Topology optimization of continuum structures：a review［J］.Appl Mech Rev，2001，54（4）：331-390

［8］Altair Engineering Inc.Altair HyperWorks version 10.0 help［EB／OL］.［2013-04-16］.http：／／www.altair.com.cn

［9］徐芝綸.彈性力學（上冊）［M］.第4版.北京：高等教育出版社，2006：257-260 Xu Zhilun.Elastic mechanics（volume 1）［M］.4th ed.Beijing：Higher Education Press，2006：257-260（in Chinese）

［10］李東澤，于登云，馬興瑞.基頻約束下的桁架結構半定規劃法拓撲優化［J］.工程力學，2011，28（2）：182-185 Li Dongze，Yu Dengyun，Ma Xingrui.Truss topology optimization with fundamental frequency constraints via semidefinite programming［J］.Engineering Mechanics，2011，28（2）：182-185（in Chinese）

［11］周志成，曲廣吉.通信衛星總體設計和動力學分析［M］.北京：中國科學技術出版社，2012：232-235 Zhou Zhicheng，Qu Guangji.System design and dynamics analysis of communication satellites［M］.Beijing：China Science and Technology Press，2012：232-235（in Chinese）