S－C型雙翼末敏彈尾翼結(jié)構(gòu)方案設計

呂勝濤，劉榮忠，郭 銳，胡志鵬

（南京理工大學 智能彈藥技術(shù)國防重點學科實驗室，南京210094）

早期末敏彈采用降落傘達到減速的目的，在此基礎(chǔ)上進行穩(wěn)態(tài)掃描。有傘末敏彈的阻力系數(shù)足夠大，可賦予彈丸充分的掃描時間，但也正因如此，易被敵方探測成為有傘末敏彈的致命弱點。而且由于降落傘的影響，有傘末敏彈極易受陣風影響而導致掃描不穩(wěn)定［1］。無傘末敏彈與之相比，具有落速高、體積小、受橫風影響小的優(yōu)點。作為未來末敏彈的發(fā)展方向，對無傘末敏彈的氣動特性分析以及尾翼參數(shù)對末敏彈氣動特性的影響研究是十分重要而且迫切的。

針對雙翼無傘末敏彈，Nadal M［2－4］提出了軸向布置增阻導旋尾翼的探測器模型，分別對尾翼固定在圓柱體底部和中部的模型進行了風洞實驗和立式風洞實驗，進而對氣動特性進行分析。胡志鵬［5－6］基于計算流體力學方法，對 S－C型、S－S型尾翼組合的末敏彈氣動外形流場進行計算，獲得了阻力系數(shù)、升力系數(shù)、轉(zhuǎn)動力矩系數(shù)和壓力中心系數(shù)隨攻角的變化規(guī)律。王愛中［7］建立了雙翼無傘末敏子彈系統(tǒng)的運動數(shù)學模型，從理論上精確描述和計算雙翼無傘末敏子彈掃描運動形成的機理。郭銳［8］設計了一種非對稱雙翼結(jié)構(gòu)彈丸的高塔投放試驗方法，分析了不同非對稱雙翼結(jié)構(gòu)對彈丸實現(xiàn)減速導旋性能的影響。在末敏彈總體優(yōu)化設計方面，黃鹍［9］應用混合遺傳算法對末敏彈仿真模型進行了優(yōu)化設計，姜禮平［10］采用遺傳算法對系統(tǒng)效能參數(shù)進行了優(yōu)化，黃風華［11］采用遺傳算法對網(wǎng)絡權(quán)值閾值進行優(yōu)化，分別獲得了影響系統(tǒng)效能的子彈落速、轉(zhuǎn)速等因素的優(yōu)化配置。綜合來看，國內(nèi)外學者對單翼模型、雙翼模型以及傘翼結(jié)合模型的研究方法大多依靠風洞試驗方法或工程模擬計算，研究內(nèi)容集中在運動機理、彈道計算等方面，尚缺乏對雙翼末敏彈的氣動外形布局與結(jié)構(gòu)優(yōu)化的系統(tǒng)研究。

對于雙翼末敏彈，希望得到盡可能大的阻力系數(shù)以確保子彈在很短的降落時間內(nèi)能迅速達到穩(wěn)定并對目標進行掃描探測，同時也要保證其下落過程中可以產(chǎn)生足以使末敏彈穩(wěn)定轉(zhuǎn)動的轉(zhuǎn)動力矩。本文選取最大阻力系數(shù)和最大極轉(zhuǎn)動力矩系數(shù)為優(yōu)化目標，對不同S－C型雙翼無傘末敏彈的翼片面積及彎折角進行了仿真計算分析。

1 氣動布局模型

S－C型雙翼無傘末敏彈的尾翼安裝在彈體尾部，由一片S形翼片和一片C形翼片組合而成，下落過程中利用2片尾翼的強非對稱實現(xiàn)穩(wěn)態(tài)掃描。

如圖1所示，末敏彈彈體為圓柱型，尺寸為φ110mm×115mm，2片尾翼彎折角按如下規(guī)則產(chǎn)生：S翼總面積記為SS，其兩外緣分別向相反方向彎折一定角度，記為βS；C翼總面積記為SC，其兩外緣向相同方向彎折一定角度，記為βC。

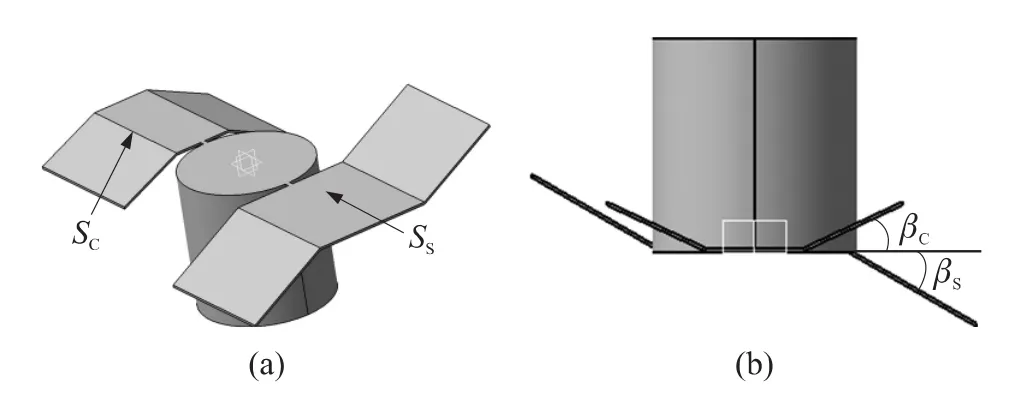
圖1 雙翼末敏彈模型

2 仿真實驗與驗證

2.1 控制方程

流體動力學要受物理守恒定律的支配，基本的守恒定律包括：質(zhì)量守恒定律、動量守恒定律和能量守恒方程。再加上必要的輔助方程，就構(gòu)成了動力學控制方程。

本文模型的控制方程包括連續(xù)性方程和動量守恒方程。其中連續(xù)方程即質(zhì)量守恒方程為

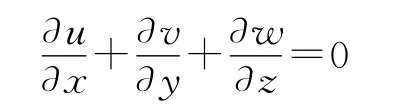
雷諾平均的N－S方程為

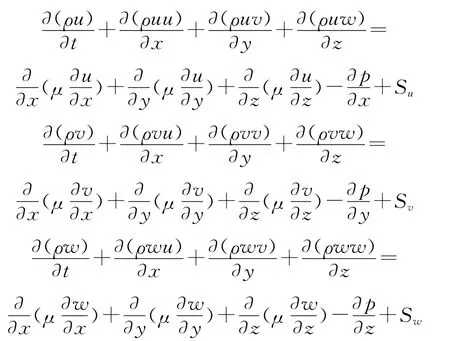
式中：u，v，w分別為流體在控制體中x，y，z3個方向上的運動速度；ρ為流體密度；p為流體微元體上的壓力；Su，Sv，Sw是動量守恒方程的廣義源項，Su＝Fx＋sx，Sv＝Fy＋sy，Sw＝Fz＋sz，F(xiàn)x，F(xiàn)y，F(xiàn)z是微元體上的體力。

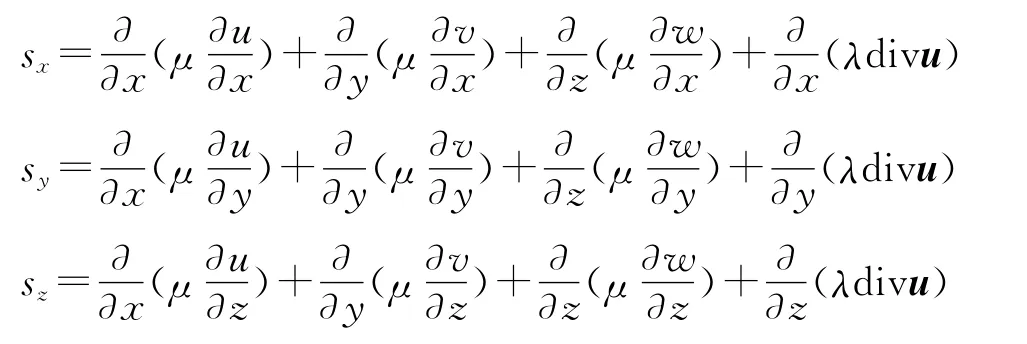
式中：μ為動力粘度，λ為第二粘度。

這里計算采用的數(shù)值模擬方法是壓力修正法（SIMPLE算法），離散方法為有限體積法。SIMPLE算法是一種求解壓力耦合方程組的半隱式方法。

湍流模型選取標準k－ε模型，控制方程為

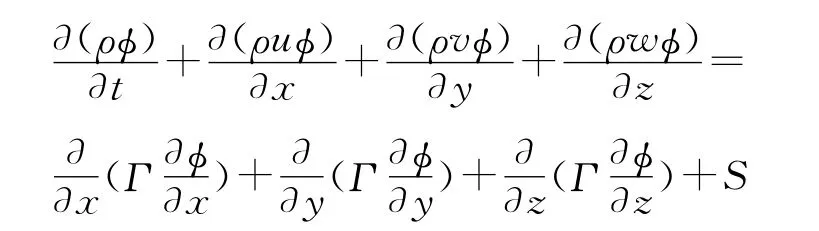
式中：φ為Reynolds平均法［12］中定義的任一變量，S為用戶定義的源項。

2.2 雙翼末敏彈流場仿真模型

用于風洞試驗的圓柱體尺寸為φ100mm×119mm，對其進行仿真計算時取流場范圍φ2 000mm×1 785mm，流場軸線與圓柱體軸線重合，圓柱體位于流場中心。靠近圓柱體處網(wǎng)格加密以保證計算精度，遠離圓柱體處網(wǎng)格密度逐漸減小以減小運算量，加快運算精度。

如圖2所示，末敏彈流場為圓柱體，為減小流場邊界影響，流場軸向取20倍彈長，徑向為15倍彈徑，即φ2 200mm×1 725mm。由于尾翼是末敏彈氣動阻力的主要來源，尾翼附近以最小間距1mm為單位劃分流場網(wǎng)格，彈體附近以最小間距2mm為單位劃分流場網(wǎng)格。在遠離彈體流場區(qū)域，以本節(jié)對圓柱體的網(wǎng)格劃分準則為標準對剩余流場進行網(wǎng)格劃分。

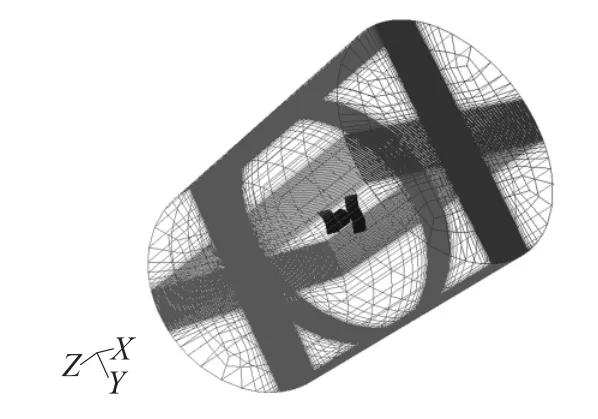
圖2 末敏彈流場網(wǎng)格

2.3 CFD仿真驗證

這里首先對圓柱型彈體進行氣動仿真分析，并與風洞試驗所得結(jié)果進行對比，得到適用于此類結(jié)構(gòu)計算時合理的Fluent參數(shù)設置。

本文對攻角分別為0°，10°，20°，25°，30°，35°，40°，45°的圓柱型彈體進行計算，計算結(jié)果及風洞試驗結(jié)果如表1所示，表中，α為攻角，Cd為阻力系數(shù)，e為誤差。

根據(jù)表1誤差列，實驗與仿真最大誤差只有12.7%左右，可見，仿真得到的阻力系數(shù)變化規(guī)律與實驗也是基本符合的。由此可認為CFD的計算結(jié)果是符合實際情況的，此例中的網(wǎng)格劃分準則及Fluent計算參數(shù)用于計算雙翼末敏彈的氣動特性所得到的結(jié)果也是可信的。

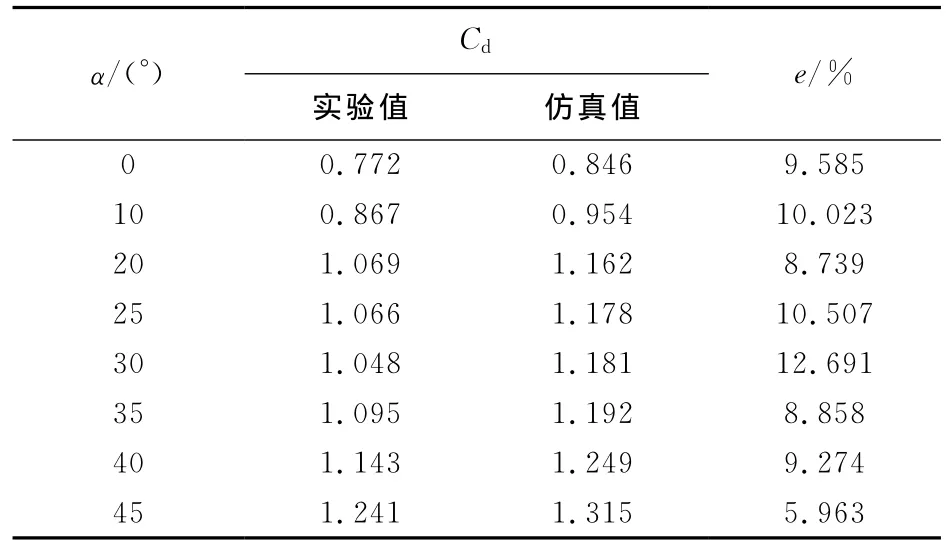
表1 不同攻角圓柱體阻力系數(shù)實驗值及仿真值

2.4 雙翼末敏彈流場特性分析

雙翼末敏彈流場特征如圖3～圖5所示。

圖3 模型表面壓力分布云圖（單位：Pa）

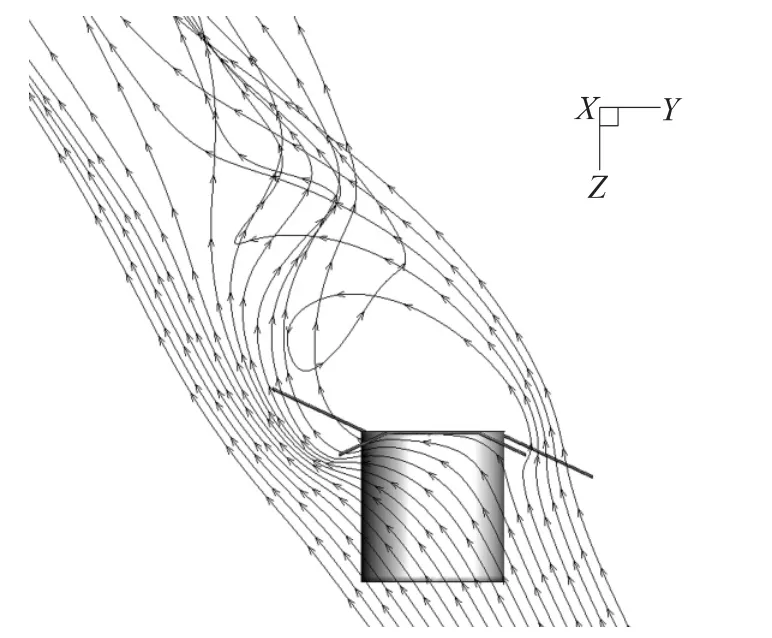
圖4 C翼迎風面速度流線圖

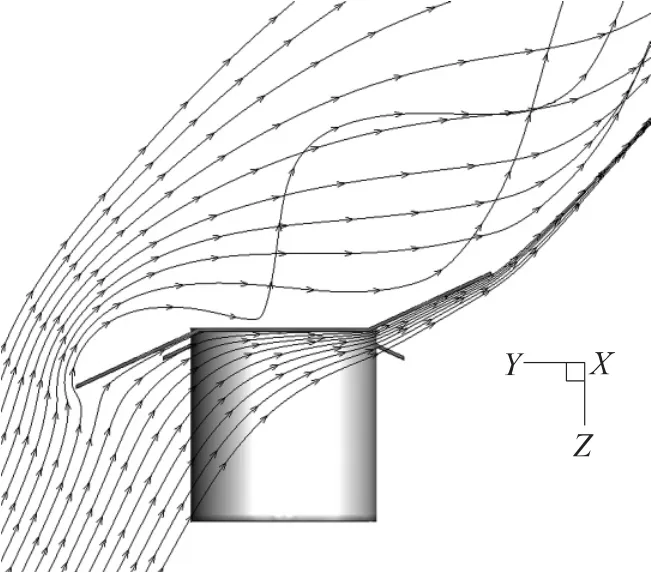
圖5 S翼迎風面速度流線圖

由圖3可見，兩尾翼的迎風面壓力很大，這是由于空氣流經(jīng)此處發(fā)生速度突變，由尾翼側(cè)面流出。正是尾翼迎風面處的壓力降低了末敏彈的下落速度，使其具有足夠的留空時間完成掃描和起爆。兩尾翼的面積不同導致氣動力的不對稱，使其彈軸能夠圍繞鉛垂線穩(wěn)定旋轉(zhuǎn)，完成穩(wěn)態(tài)掃描。可見尾翼面積和彎折角對末敏彈氣動特性的重要作用。由圖4、圖5流線圖可見，尾翼彎折角對氣流的影響很大，對其合理優(yōu)化是十分必要的。

3 正交優(yōu)化試驗設計

本文取S翼面積、C翼面積、S翼彎折角、C翼彎折角4個參量各3個水平進行優(yōu)化計算，分別記為SS，SC，βS，βC，即4因素3水平的試驗，采用正交試驗［12］方法進行優(yōu)化試驗設計。由于雙翼末敏彈下落時攻角在30°左右［6］，仿真過程保持攻角30°不變。SS的3個水平分別為286cm2，297cm2，242cm2，分別記為該因素下的1，2，3；SC的3個水平分別為165cm2，176cm2，187cm2，分別記為該因素下的1，2，3；βS的3個水平分別為25°，30°，35°，分別記為該因素下的1，2，3；βC的3個水平分別為25°，30°，35°，分別記為該因素下的1，2，3。4個變量及其水平如表2所示。以L9（34）正交表安排各因素和各水平，如表3所示。以所列9種組合仿真計算末敏彈的阻力系數(shù)和極轉(zhuǎn)動力矩系數(shù)。這里以課題組所設計某一氣動結(jié)構(gòu)末敏彈為待優(yōu)化模型，其特征尺寸分別為SS＝286cm2，SC＝176cm2，βS＝30°，βC＝30°。

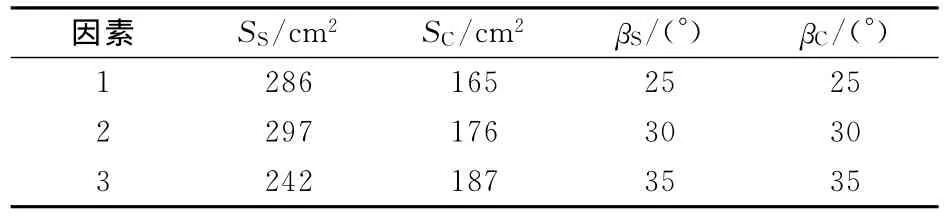
表2 試驗因素的水平設置

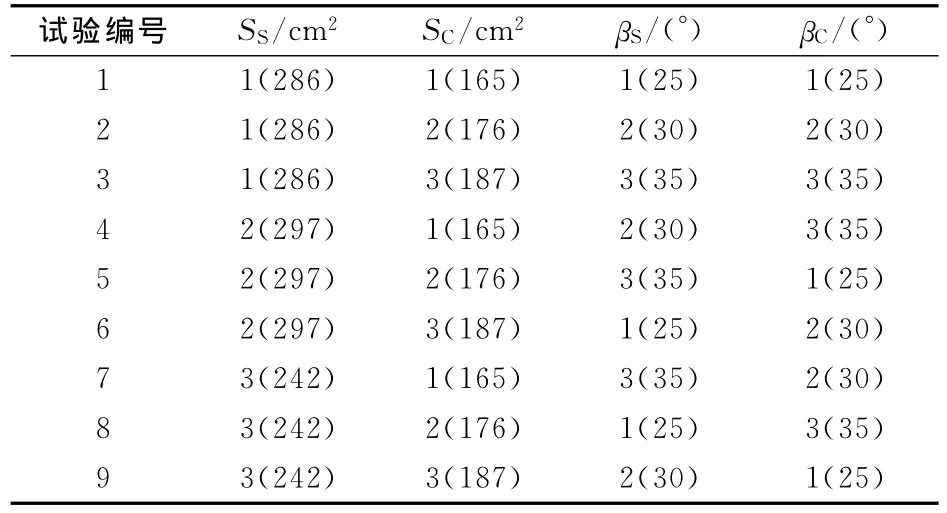
表3 正交試驗設計表

4 優(yōu)化結(jié)果與討論

表4所示為正交試驗所得的仿真值，表中Cm為極轉(zhuǎn)動力矩系數(shù)，表5、表6所示為正交試驗分析結(jié)果，均值表示對應列所對應的因素在該水平下的指標值的平均值，極差行表示均值的極差，用以指示各因素對阻力系數(shù)影響的主次關(guān)系。

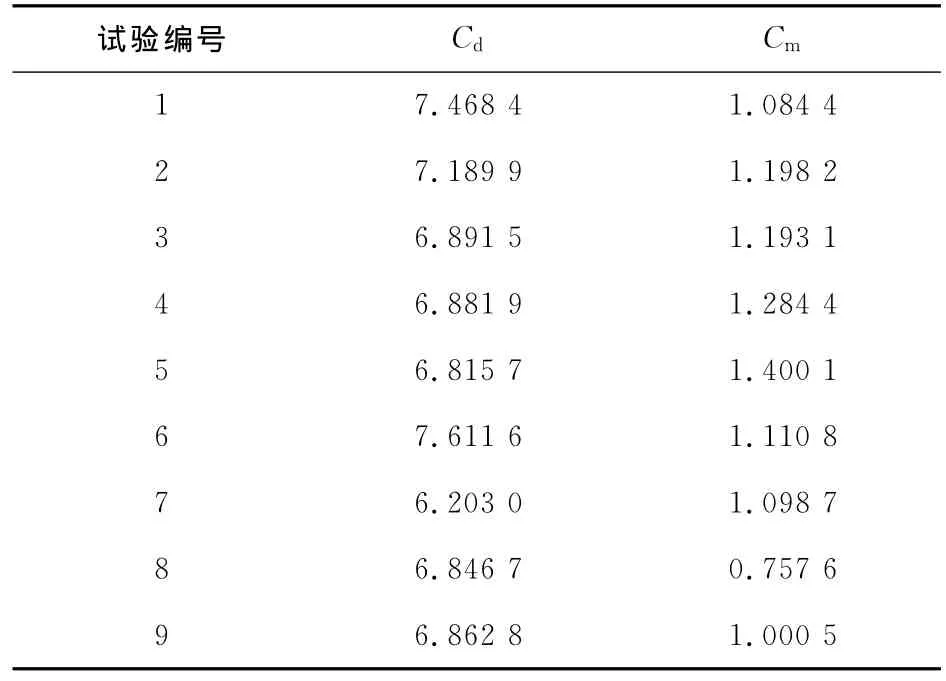
表4 正交試驗結(jié)果

1）阻力系數(shù)。

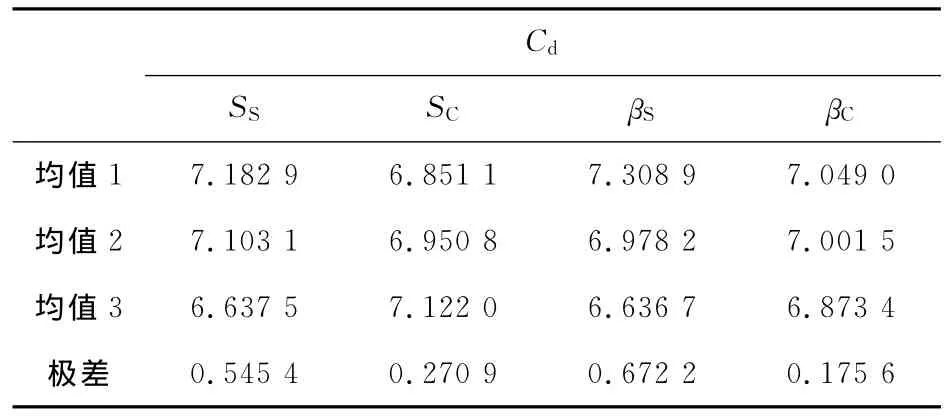
表5 正交試驗阻力系數(shù)結(jié)果分析

由表5極差分析，對末敏彈阻力系數(shù)影響最大的是βS，其次是SS，再次是SC，βC影響最小。最佳方案為SS1SC3βS1βC1。

2）極轉(zhuǎn)動力矩系數(shù)。

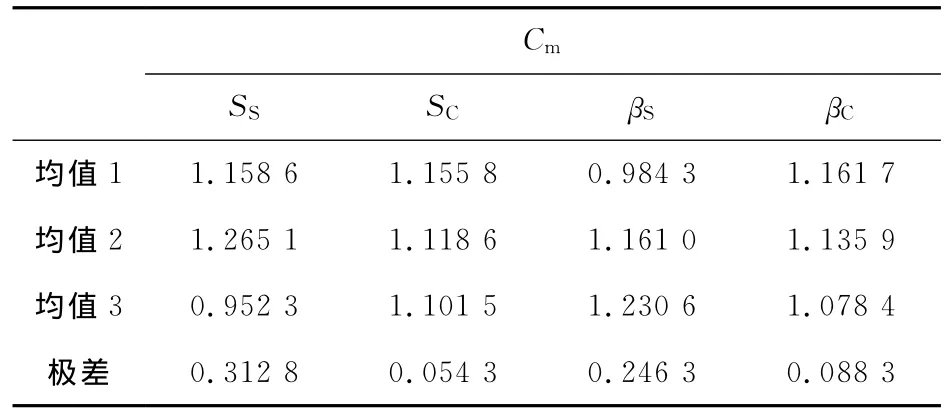
表6 正交試驗極轉(zhuǎn)動力矩系數(shù)結(jié)果分析

通過表6極差分析，對末敏彈極轉(zhuǎn)動力矩系數(shù)影響最大的是SS，其次是βS，再次是βC，SC影響最小。最佳方案為SS2SC1βS3βC1。

3）最佳氣動外形的確定。

本文的優(yōu)化目標是滿足最大阻力系數(shù)及極轉(zhuǎn)動力矩系數(shù)，其中以阻力系數(shù)為優(yōu)先選項。二者之間可能存在一定的矛盾，如當滿足最大阻力系數(shù)時，SC應取最大值，若滿足最大極轉(zhuǎn)動力矩系數(shù)，SC應取最小值。這時需要兼顧2個目標，尋找使二者都能盡可能大的翼片組合方式，這里運用多指標處理方法中的綜合平衡法對優(yōu)化結(jié)果進行選取。

由于βS對阻力系數(shù)影響最大，應首先加以分析；SS對極轉(zhuǎn)動力矩系數(shù)影響最大，次要分析；SC和βC對2個優(yōu)化目標影響均不大，最后分析。最終確定分析先后順序為βS—SS—βC—SC。

由表5及表6可見，βS取最小值時，阻力系數(shù)最大；取最大值時，極轉(zhuǎn)動力矩系數(shù)最大，這里取βS為30°。由結(jié)果分析可見，SS取286cm2和297cm2時的阻力系數(shù)和極轉(zhuǎn)動力矩系數(shù)相差不多，這里優(yōu)先滿足阻力系數(shù)的要求，取SS為286cm2。βC取25°時阻力系數(shù)和極轉(zhuǎn)動力矩系數(shù)均達到最大值。SC取最大值時，阻力系數(shù)最大，取最小值時，極轉(zhuǎn)動力矩系數(shù)最大，而SC取187cm2和165cm2時的阻力系數(shù)和極轉(zhuǎn)動力矩系數(shù)相差不大。這里以阻力系數(shù)為優(yōu)先考慮目標，取SC為187cm2。由此，得到最終優(yōu)化結(jié)果為SS1SC3βS2βC1。但這一組合在正交表中并未出現(xiàn)，故需要對這一組合的末敏彈流場重新進行網(wǎng)格劃分并計算。加試計算結(jié)果見表7。

表7 加試模型計算結(jié)果

由表7可見，通過正交試驗得到了雙翼末敏彈的最佳外形，此優(yōu)化模型能同時滿足阻力系數(shù)和極轉(zhuǎn)動力矩系數(shù)的要求。

由表3可見，初始尾翼結(jié)構(gòu)正是正交表中的組合2。優(yōu)化模型阻力系數(shù)增加5.14%，極轉(zhuǎn)動力矩系數(shù)增加4.53%。

5 高塔試驗驗證

通過仿真得到了一種尾翼優(yōu)化結(jié)構(gòu)，即SS＝286cm2，SC＝187cm2，βS＝30°，βC＝25°。為進一步驗證所得優(yōu)化結(jié)構(gòu)是否滿足在下落過程中保持穩(wěn)定不翻轉(zhuǎn)，對仿真計算所得的氣動外形加工樣彈進行高塔自由飛行試驗。

如圖6所示，優(yōu)化后的模擬彈彈體為圓柱體，直徑110mm，高115mm，總質(zhì)量4.2kg，在彈尾安裝S－C型尾翼。模擬彈自高100m的高塔塔頂自由投放，垂直于塔壁懸掛高度標志物，如圖7所示，兩兩間隔及距地距離已知，由高速攝影儀記錄樣彈飛行過程。圖8所示為模擬彈轉(zhuǎn)動一周的飛行姿態(tài)，可見模擬彈彈軸是以鉛垂線為軸轉(zhuǎn)動，模擬彈同時圍繞彈軸轉(zhuǎn)動，轉(zhuǎn)動過程中模擬軸與鉛垂線始終存在一個角度，即末敏彈的掃描角。可見，優(yōu)化結(jié)構(gòu)能滿足穩(wěn)定性要求，在下落過程中保持穩(wěn)定。

圖6 樣彈模型

圖7 自由飛行試驗

圖8 樣彈轉(zhuǎn)動一周飛行姿態(tài)

6 結(jié)論

本文基于正交試驗方法，對現(xiàn)有不同尾翼組合進行分組仿真計算，得到滿足最大阻力系數(shù)和最大極轉(zhuǎn)動力矩系數(shù)的尾翼組合。

通過對雙翼末敏彈的仿真計算，對雙翼末敏彈阻力系數(shù)影響最大的是S翼彎折角，其次為S翼面積，再次為C翼面積，C翼彎折角的影響最小；對極轉(zhuǎn)動力矩系數(shù)影響最大的是S翼面積，其次為S翼彎折角，再次為C翼彎折角，C翼面積的影響最小。

通過正交試驗設計，得到一種可同時滿足阻力系數(shù)和極轉(zhuǎn)動力矩系數(shù)要求的最佳尾翼組合雙翼末敏彈氣動外形，阻力系數(shù)較優(yōu)化前增加5.17%，極轉(zhuǎn)動力矩系數(shù)增加4.53%。

本文針對無傘末敏彈只研究了阻力和轉(zhuǎn)動力矩的計算方法，這對于研究無傘掃描運動的形成和特性只是起步，但還遠遠不夠，進一步還需要研究靜穩(wěn)定力矩、俯仰阻尼力矩、滾轉(zhuǎn)阻尼力矩的計算并分析它們的作用，這些工作將在下面繼續(xù)進行。

［1］何喜營.國外末敏彈藥的發(fā)展現(xiàn)狀及前景分析［J］.彈箭技術(shù)，1995（2）：1－11.HE Ying－xi.The present situation and prospect of foreign terminal sensing ammunition［J］.Projectile ＆ Rocket Technology，1995（2）：1－11.（in Chinese）

［2］VICENTE N M，ANGEL S A，ALVARO C.Model of the aerodynamic behavior of a pararotor［J］.Journal of Aircraft，2006，43（6）：1－15.

［3］VICENTE N M，ANGEL S A，ALVARO C.Experimental investigation of an autorotating－wing aerodynamic decelerator system［C］／／18th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar.Munich，Alemania：AIAA，2005：1－15.

［4］VICENTE N M，PIECHOCKI J，CUERVA A，et al.Experimental research on a vertically falling rotating wing decelerator model［C］／／19th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar.Williamsburg，VA：AIAA，2007：2 568－2 583.

［5］胡志鵬，劉榮忠，郭銳.基于FLUENT的雙翼末敏彈氣動特性研究［J］.飛行力學，2013，31（1）：53－60.HU Zhi－peng，LIU Rong－zhong，GUO Rui.Aerodynamic characteristics of two wings terminal sensitive projectile based on Fluent［J］.Flight Dynamics，2013，31（1）：53－60.（in Chinese）

［6］胡志鵬，劉榮忠，郭銳.兩種典型尾翼形狀對無傘末敏彈氣動特性的影響［J］.南京理工大學學報，2010，36（5）：739－744.HU Zhi－peng，LIU Rong－zhong，GUO Rui.Effect of two－typical wing shapes on aerodynamic characteristics of non－parachute terminal－sensitive projectile［J］.Journal of Nanjing University of Science and Technology，2010，36（5）：739－744.（in Chinese）

［7］王愛中.無傘末敏彈穩(wěn)態(tài)掃描特性研究［D］.南京：南京理工大學，2008.WANG Ai－zhong.Research on the stable scanning motion of the terminal－sensitive ammunition with two wing panels［D］.Nanjing：Nanjing University of Science and Technology，2008.（in Chinese）

［8］郭銳，劉榮忠，王本河，等.一種非對稱雙翼結(jié)構(gòu)彈丸減速導旋特性試驗研究［J］.彈箭與制導學報，2009，29（5）：249－254.GUO Rui，LIU Rong－zhong，WANG Ben－h(huán)e，et al.Experimental study on decelerating and spinning characteristics of an asymmetric two－wing projectile［J］.Journal of Projectiles，Rockets，Missiles and Guidance，2009，29（5）：249－254.（in Chinese）

［9］黃鹍，陳森發(fā)，劉榮忠.基于神經(jīng)網(wǎng)絡和遺傳算法的末敏彈系統(tǒng)效能參數(shù)優(yōu)化設計［J］.兵工學報，2004，25（3）：257－260.HUANG Kun，CHEN Sen－fa，LIU Rong－zhong.Optimal design of system efficiency parameters about terminal－sensitive－projectiles based on neural network and genetic algorithm［J］.Acta Armamentarii，2004，25（3）：257－260.（in Chinese）

［10］姜禮平，張緒春，王平.基于支持向量機和遺傳算法的末敏彈系統(tǒng)效能參數(shù)優(yōu)化設計［J］.海軍工程大學學報，2007，19（1）：32－34.JIANG Li－ping，ZHANG Xu－chun，WANG Ping.Optimal design of system efficiency parameters about terminal sensitive projectiles based on support vector machine and genetic algorithm［J］.Journal of Naval University of Engineering，2007，19（1）：32－34.（in Chinese）

［11］黃風華，劉榮忠，郭銳.基于混合神經(jīng)網(wǎng)絡的末敏彈系統(tǒng)參數(shù)優(yōu)化設計［J］.計算機仿真，2012，29（3）：53－56.HUANG Feng－h(huán)ua，LIU Rong－zhong，GUO Rui.Optimal design of system efficiency parameters about terminal－sensitiveprojectiles based on hybrid neural network［J］.Computer Simulation，2012，29（3）：53－56.（in Chinese）

［12］葉慈南，曹偉麗.應用數(shù)理統(tǒng)計［M］.北京：機械工業(yè)出版社，2004：279－290.YE Ci－nan，CAO Wei－li.Applied mathematical statistics［M］.Beijing：China Machine Press，2004：279－290.（in Chinese）