留預備隊的思想與預備隊最佳預留方案研究

嚴建鋼 楊士鋒

(海軍航空工程學院，山東 煙臺264001)

1 引言

戰斗是具有主觀能動性的雙方之間進行的對抗。為了取得優勢并利用優勢取得勝利，戰斗雙方總是力圖采取一些對方預料之外的策略。正因為如此，在戰斗中，并不是所有的情況都可以預料得到:有些情況預料到了但沒有發生，有些情況沒有預料到卻發生了。預備隊就是為了應付這些意外情況而專門組建的預備力量，對于預備隊的運用是作戰決策迫切需要研究與解決的問題。

目前，關于預備隊預留問題的把握，主要是根據我軍豐富的作戰經驗，按照總兵力的一定比例進行掌握與控制［1］。這種方法處理問題簡單，宏觀性強，對指導我軍作戰確實起到了很大的作用。但是，在敵方兵力變化或在己方兵力緊張的情況下，這種按一定比例預留的原則是否還適用呢?本文針對這個問題，根據蘭徹斯特方程、作戰理論以及運籌學原理，提出了戰爭(戰斗)預備隊力量使用最佳方案的概念，并建立了預備隊最佳預留模型，解決了在有限資源的情況下合理使用戰爭(戰斗)各種力量的問題，使有限的資源發揮最大的效益。

2 留預備隊思想的數理剖析

本文以一個實際的數值例子，用多戰場的蘭徹斯特方程來說明留預備隊的策略是一種好的策略［2，3］。

2.1 問題描述

假定甲、乙雙方發生一場戰斗，乙方擬向甲方進攻，可能的戰場有三個:主要進攻方向1，也即主要防御方向1;次要進攻方向2，也即次要防御方向2;甲方的大本營3。在大本營處交戰有利于乙方進攻而不利于甲方堅守，所以乙方只要在主要進攻方向1 或次要進攻方向2 上有一處突破，就可長驅直入進攻甲方的大本營3，而甲方則要分兵把守主要防御方向1 與次要防御方向2，使其不能突破防線，一旦發現有一處吃緊，就可將留在大本營的預備隊派往該處防守。現在進一步假定雙方都為單兵種作戰，乙方集中全部初始兵力于主要進攻方向1 或者次要進攻方向2，在另一個方向的佯攻或牽制等部隊不明顯地反映在模型中。事先甲方并不知道乙方的企圖究竟是在哪一個方向進攻，甲方初始兵力x0中分x10于主要防御方向1，x20于次要防御方向2，留x30= x0-x10-x20于大本營。一旦發現乙方向主要進攻方向1 攻擊時，甲方就將預備隊x30全部派往方向1，在T1時間后即可到位作戰;一旦發現乙方向次要進攻方向2 攻擊時，甲方就將預備隊x30全部派往方向2，在T2時間內即可到位作戰。大本營的直接保衛、警戒部隊等另行留出，也不明顯地反映在模型中。已經部署到次要防御方向2 的部隊x20由于種種原因，不能增援方向1。同樣已經部署到主要防御方向1 上的部隊也不能增援方向2。

如果取x30=0，就是不留預備隊;如果取x10=x20=0，就是固守大本營，不在主要防御方向1 與次要防御方向2 部署防御力量。這兩種極端情況可以作為一般情況的對比，現在的問題是如何分配x10、x20與x30，使甲方在抗擊乙方進攻時效果更好。

2.2 蘭徹斯特建模分析

進一步假定在三個不同戰場交戰的蘭徹斯特方程如下:

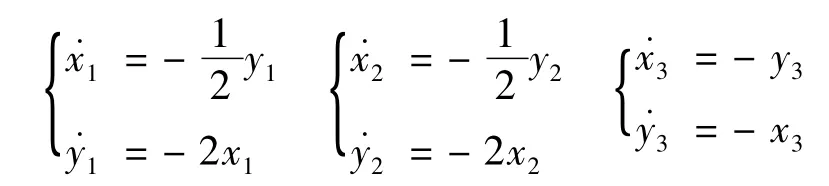
初始兵力x0=10000，y0=12000，T1= T2=

ln1.25。

例子中所有參數的選擇，特別是戰場1 與戰場2 參數的一致性，都是為了說明問題與討論方便起見精心選取的，但其結論仍不失普遍性。現討論以下三種方案。

2.2.1 方案1

甲方不留預備隊，即取x10= x20=5000，x30=0。

假定乙方集中全力從主要方向1 進攻，則在戰場1 的蘭徹斯特方程的解為:

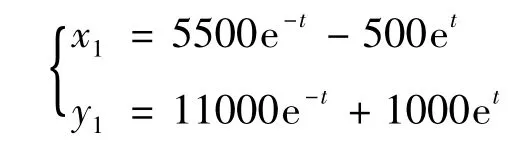
在這種部署下，甲方不能有效抵抗乙方的進攻，可以證明，該方案下甲方最多能有效抵抗乙方初始兵力y0=10000 的進攻。

2.2.2 方案2

甲方全部留在大本營，即取x10= x20=0，x30=10000。

這時乙方可輕易通過戰場1、2 中任意一個方向進攻，直接到甲方大本營決戰，此時在戰場3 的蘭徹斯特方程的解為:

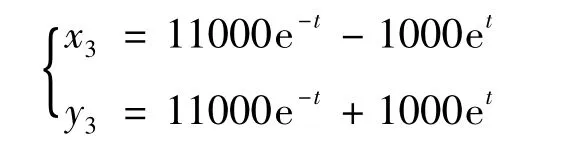
甲方對兵力適當配置，取x10= x20=3000，x30=4000。

假定乙方將全部兵力用于戰場1，則開始時戰場1 的蘭徹斯特方程的解為:

戰斗開始后，甲方知道戰場1 吃緊就將全部預備隊x30派往戰場1，經時間T1=ln1.25 后到達戰場1。在預備隊到達前的瞬間:

當預備隊到達后，甲方實力變為:

乙方實力不變。從T1時刻起算，戰場1 處的蘭徹斯特方程的解為:

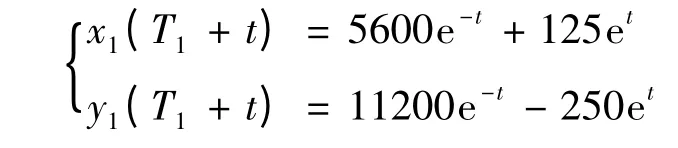
顯然這時乙方不能突破主攻方向，甲方有效地抵抗了乙方的進攻。這種情況下，若乙方在主要進攻方向1 與次要進攻方向2 上分兵進攻顯然效果更差。

對以上三種作戰部署方案的分析說明，無論是傾巢分兵把守還是全部留守，都不能抵御敵方的進攻，只有適當留預備隊才是克敵制勝之道。這一結論與軍事常識中留預備隊的戰術是一致的［4-6］。

3 預備隊投入時的作戰模型

為了說明預備隊的使用對作戰勝負的關鍵作用，盡量減少雙方戰術優劣等其他因素對作戰的影響，可將雙方兵力都看作一個整體，使用單兵種作戰的蘭徹斯特方程。假設甲、乙雙方交戰，甲方投入兵力的初始值為x0，且一次性投入戰斗;乙方共有兵力為y0，且分期分批投入，這就是一個預留預備隊的問題。針對這一特點，下面討論一方留有預備隊的作戰模型。

設乙方留有一部分預備隊兵力，在一定時間T內，按一定補充速度K投入戰斗，其他條件不變，那么雙方的作戰模型為:

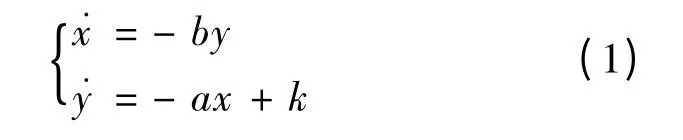
這時乙方兵力的初始條件y00為:總的投入兵力y0與在此模型下作戰時間T內補充兵力K·T之差。即:

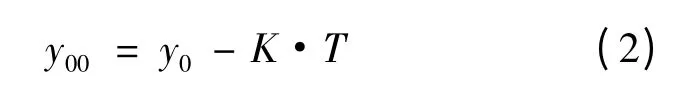
定理1:設甲、乙雙方作戰，甲方全力展開攻擊乙方，乙方留取一定的兵力作為預備隊，逐次展開增援，雙方的初始實力為x(0)= x0，y(0)= y00=y0-K·T，則留預備隊的作戰模型(1)有唯一解為:

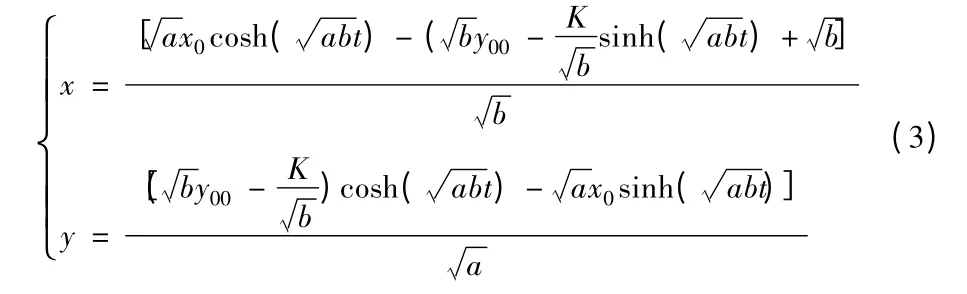
［7］中定理3.1，可得到式(3)。

設:

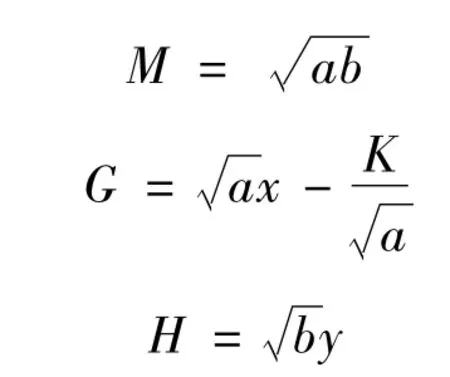
則由式(1)得:

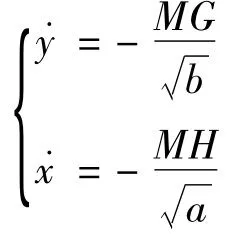
變形為:

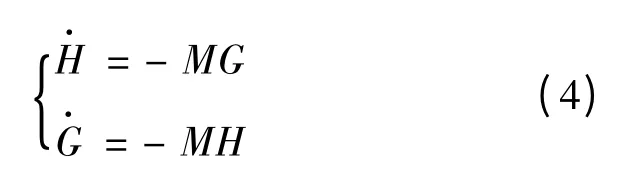
式(4)在形式上與參考文獻［7］中定理3.1 完全相同，從參考文獻［7］的定理3.2 知，甲方要取得勝利，必須是使

成立，而留預備隊作戰模型，甲方獲勝條件是:

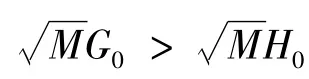
即:

將式(2)代入得:

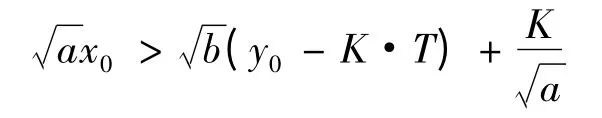
將參考文獻［8］中3.6 代入得:

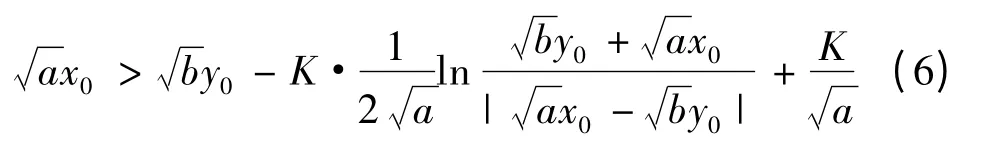
設:

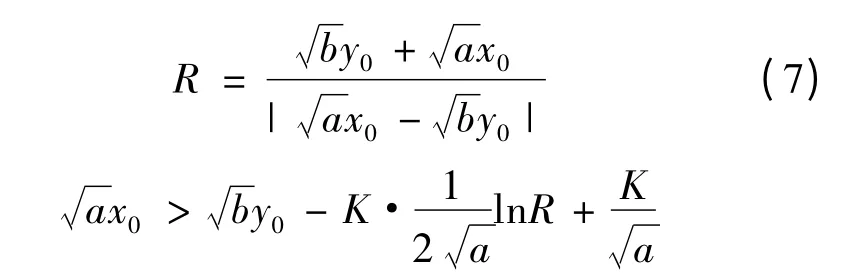
再設:

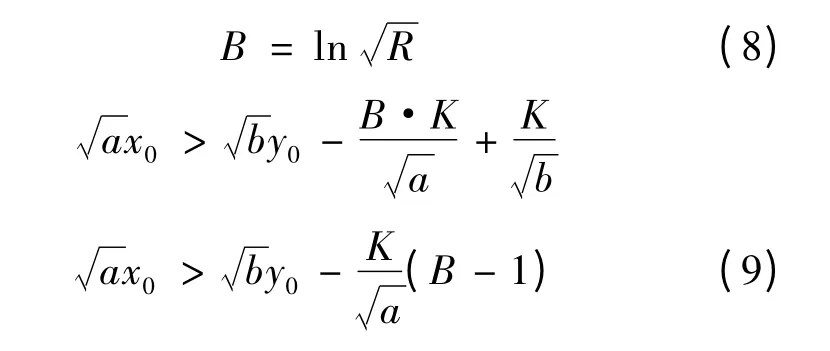
式(9)說明在乙方留有預備隊逐次展開增援的情況下，甲方獲勝的條件發生了變化，這是一個重要的發現，對研究是否留預備隊以及怎樣留提供了依據。

4 預備隊預留的最佳模型

式(9)與式(5)相比，差別在于不等式右邊反映乙方實力的數值發生了變化，說明了留不留預備隊確實影響雙方作戰實力的表現程度，從而影響作戰進程與結果，這是一個重要的作戰決策問題。

對式(7)進一步分析可以得出許多有價值的信息。式(9)與式(5)相比的變化項是:

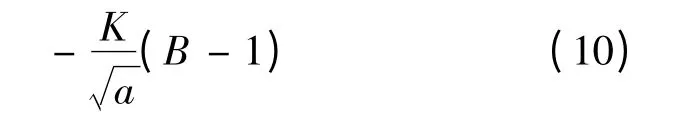
式(10)中，K與a分別是乙方預備隊的增援速度、甲方攻擊乙方的威力系數，它們都是大于0 的參數，那么式(10)的符號就取決于B的取值情況。

當B ＜1 時，式(10)始終是一個大于0 的數，說明乙方總的作戰實力是增加了，按照這種方式預留預備隊是一種好的策略。

當B ＞1 時，式(10)始終是一個小于0 的數，說明乙方總的作戰實力是減小了，按照這種方式預留預備隊是一種壞的策略，不但沒有增加實力，反而減小己方的作戰能力，把可能到手的勝利拱手讓給了對方，得不償失。

當B =1 時，式(10)始終為0，雙方的實力都沒有發生變化，這種預留預備隊的方案是好是壞，不能籠統地下結論，必須根據具體情況加以分析。

從以上三種情況分析可以看出，B值全面反映了留預備隊可能出現的各種情況，下面根據式(8)，分析各種預留預備隊方案的利與弊。

從式(8)中可以看出B值的取值情況又取決于R值，而R值取決于式(7)，即:

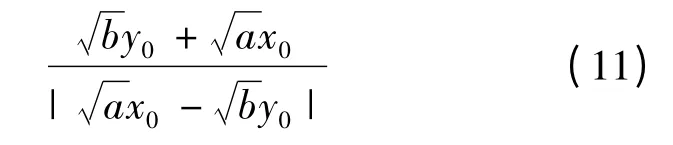
定義1:甲、乙雙方按照單兵種對單兵種交戰，雙方的殺傷系數為a、b，雙方初始投入兵力為x0、y0，稱R為交戰雙方實力差強度函數。當＞0 時，稱R為正強度函數;當時，稱R為負強度函數;當時，稱R為無差別度函數。

實力差強度函數R的大小直接反映B的取值情況，根據式(8)看出B值隨R函數呈自然對數規律變化，可以通過調整R值的大小，來調整B值的大小。

定義2:甲、乙雙方交戰，一方全力以赴展開兵力交戰，一方按照一定的預留兵力持續展開進行交戰，由實力差強度函數R確定的B，我們稱為預備隊預留值比較函數，由此確定的模型(9)稱為預備隊預留判斷模型。

通過對預備隊預留判斷模型(9)的分析，可以得到在一定的作戰態勢下是否留預備隊，留多少。如不具備條件，是否調整兵力投入，預留一定數量的預備隊，達到最佳作戰效果。下面用定理的形式給出。

定理2:設甲、乙雙方作戰，甲方全力展開攻擊乙方，乙方留取一定的兵力作為預備隊，逐次展開增援，雙方的初始實力為x(0)= x0，y(0)= y00=y0-K·T，則當時，可以預留一部分兵力為預備隊，其預留兵力yl為:

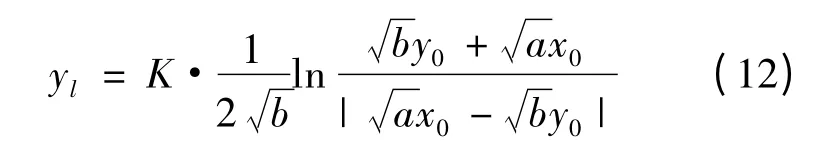
式(12)中K可以根據作戰的實際需要，由指揮員確定。當B =ln ■R ＞1 時，不宜留預備隊，如特別需要留有一部分預備隊，則通過調整兵力的投入y0，使yl達到:

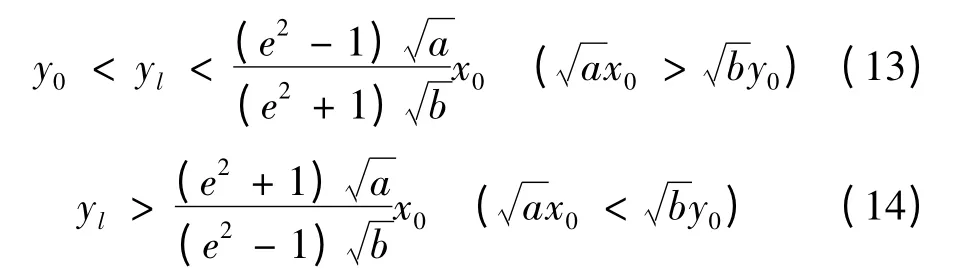
當B =ln ■R =1 時，可以根據戰場的實際情況確定留不留預備隊和預留預備隊的具體方案。

定理2 說明了一個非常重要的戰術思想，在兵力一定的情況下留不留預備隊主要取決于交戰雙方實力差強度函數R。R值較大時，說明戰場上力量弱的一方承受壓力較大，如果這時再分配一定比例的兵力留作預備隊，勢必加大己方戰場上的壓力，預備隊預留值比較函數B增加，總體上削弱己方總的作戰能力，影響全局作戰的效果。只有在強度函數R值較小時，說明戰場上力量弱的一方承受壓力較小，如果這時分配一定比例的兵力留作預備隊持續展開攻擊對方，預備隊預留值比較函數B減少，總體上增加己方總的作戰能力，可以使作戰資源的能力充分發揮出來，取得最佳的作戰效果。

5 結論

利用比較函數B確定預備隊預留的策略，不但考慮了己方兵力的情況，而且還考慮了敵方的兵力情況，將敵我雙方的兵力綜合起來進行定量考慮，使預備隊的預留兵力建立在科學分析計算的基礎上，做到了定性與定量、經驗與理論相結合。本文中比較函數B的推導是建立在蘭徹斯特“平方率”方程基礎上，如果能夠建立信息化條件下的蘭徹斯特方程，比較函數B也適用于信息化條件下預備隊預留方案的制定。

參考文獻

1 江寧.高級戰術學導論［M］.北京:解放軍出版社，2011.

2 薛興林.戰役理論學習指南［M］.北京:國防大學出版社，2002.

3 國防大學.戰役學［M］.北京:國防大學出版社，2000.

4 劉金勝.戰役［M］.北京:中國大百科全書出版社，2007.

5 宋曉軍.中外著名戰役［M］.北京:星球地圖出版社，2012.

6 Eastern RAND Report.美軍專家探討戰役預備隊的過去，現在與未來［J］.國際防務譯文，2011(14):6 -13.

7 沙基昌.數理戰術學［M］.北京:科學出版社，2003.

8 嚴建鋼.航空兵數理戰術分析［M］.北京:解放軍出版社，2006.