穿孔板聲特性的數值模擬和試驗研究

寧玉恒，楊 丹

NING Yu-heng1, YANG Dan2

（1.大唐東北電力實驗研究所有限公司，長春 130021；2.吉林農業大學，長春 130118）

0 引言

在噪聲控制工程中，穿孔板共振結構是一種常用的吸聲結構[1]，目前已廣泛應用于高速列車和客車的頂部以及發動機的消聲器中[2]。對穿孔板吸聲結構的研究目前主要集中在理論和試驗階段，馬大猷推導了穿孔板吸聲結構的理論[3]，劉克從試驗著手研究了擴散場內穿孔板的吸聲特性[4]，在穿孔板聲輻射效率方面的研究幾乎處于空白。

現階段對穿孔板進行數值仿真的研究相對比較少，在理論和試驗比較成熟的情況下，數值模擬可以節約時間，降低成本。擬采用邊界元方法對穿孔板的隔聲性能進行仿真，并與試驗進行對比，驗證了此種方法的可行性。穿孔板聲輻射效率已無法使用傳統的聲振法測試，鑒于此，嘗試采用單元分離法進行測量，單元分離法在工程中的應用也很少，李民等人使用單元分離法測量發動機齒輪罩的聲輻射效率[5]。最終結果表明，通過單元分離法可以準確獲得穿孔板的聲輻射效率。

1 穿孔板有限元模型的建立

穿孔板的尺寸是840mm×7000mm×1.7mm，由于較薄，采用三維建模會影響網格質量，因而采用殼單元劃分網格，然后賦予結構厚度。由于孔的尺寸相對截面尺寸很小，建模時，如果對小孔進行處理，網格質量將會降低，計算精度難以保證，因此，在劃分網格時，將所有孔密封處理，通過賦予導納屬性來模擬小孔，有限元模型如圖1所示，共有167964個殼單元。

圖1 穿孔板的有限元模型

2 阻尼損耗因子測試

結構動力學特性的影響因素除了系統的質量和剛度，還有阻尼損耗因子。為了獲取穿孔板的阻尼損耗因子，試驗采用脈沖衰減法[6,7]進行了測試，測試裝置示意圖如圖2所示，將穿孔板用柔性繩懸掛，滿足構件受激后自由振動[8]。選取合理的位置布置六個振動加速度傳感器，用力錘在多個位置進行瞬態激勵，記錄各測試點的振動衰減過程，最后結合先進的數據處理方法，識別得到穿孔板的阻尼損耗因子，如圖3所示，穿孔板在1000Hz以內的內損耗因子為0.15%～0.35%。

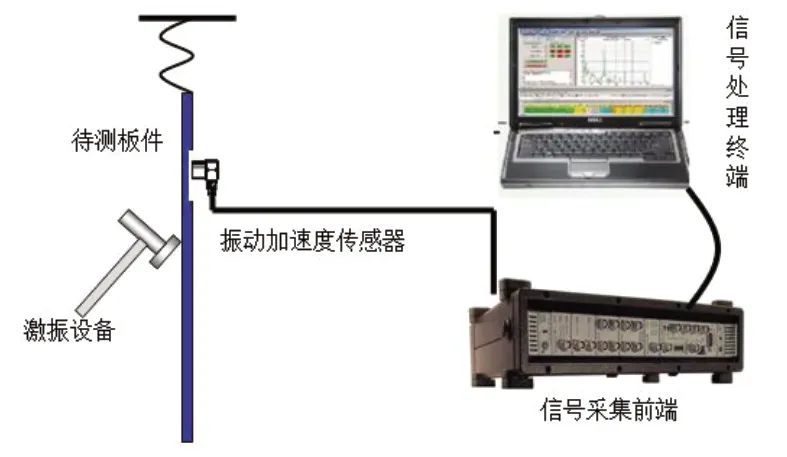
圖2 阻尼損耗因子測試示意圖

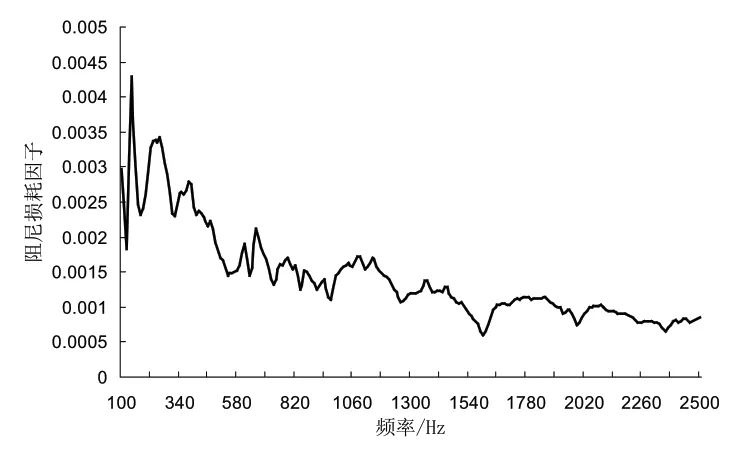
圖3 穿孔板的阻尼損耗因子

3 導納的求解

如上所述，穿孔板在聲學計算時，由于存在很多小孔，使得有限元網格的劃分非常困難，如果把網格劃分得非常細致，那么網格的數量會非常巨大，同時網格質量也會非常差，以至于不能計算。為了解決小孔的問題，在穿孔板兩邊的網格之間通過定義傳遞導納來模擬這些小孔。

聲阻抗的表達式為：

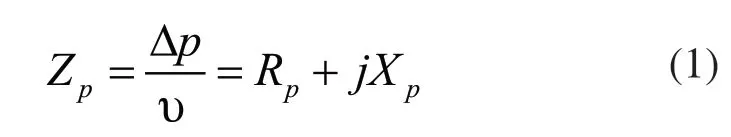
式中，Δp 是聲音通過穿孔板前后的聲壓差；υ是小孔處的振動速度。我們能通過Mechel公式來計算得到阻抗ZP。Mechel公式如下所示：

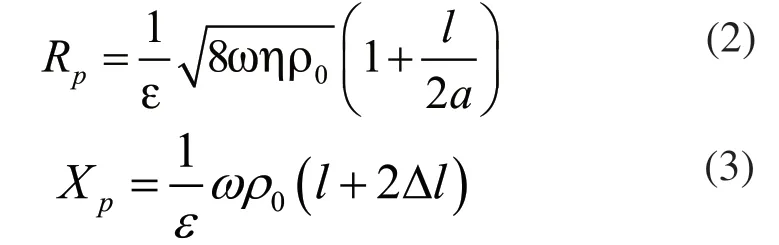
孔隙率ε表示如下：

式中，n 為圓孔的個數；a 為圓孔的體積；S為穿孔板的橫截面積；t為穿孔板的厚度。

在工程實際中，圓孔的排列方式主要有正方形和正六邊形兩種排列方式。文中所述的圓孔排列方式是長條形排列的，但是康鐘緒等人研究表明，圓孔的排列方式對修正厚度的影響很小[9]，因此可以借鑒正方形排列方式的計算公式獲得修正厚度：

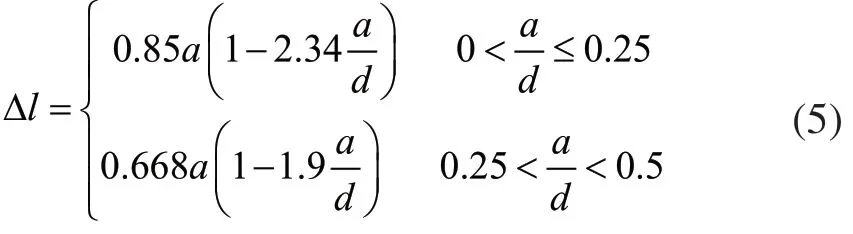
式中，d為兩相鄰圓孔中心的距離。

在Virtual.Lab聲學計算軟件中，穿孔板是通過定義一個傳遞導納矩陣來表示的，該矩陣如下：

其中，系數k考慮了穿孔板的厚度對穿孔板兩側面積的影響，即k為穿孔板上下截面積的比值，在文中可以取1；。

進行聲學計算時，由于不同頻率下傳遞導納的數值不一樣，因此我們需要獲得一系列的導納值。穿孔板兩側的振動速度和聲壓的傳遞導納關系用以下公式來表示：

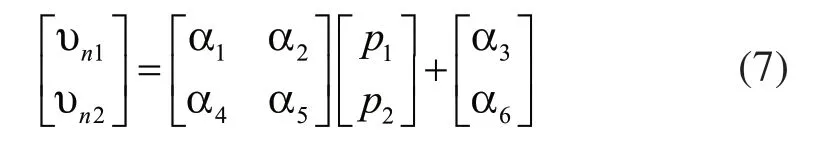
其中，υ1n和υn2是穿孔板兩側的法向振動速度；p1和 p2為穿孔板兩側的聲壓；α1、α2、α4、α5為傳遞導納系數，其值就是上式的矩陣，前文表明，系數k取1，因此 α1=α5，α2=α4，α3和 α6是由聲源確定的，在試中均為0，因此只要計算出導納，就可以知道振動速度和聲壓的關系，進一步獲得其他聲學參數。

將各個參數代入上式中，可以獲得各頻率下的導納值，導入軟件進行計算。

4 穿孔板的隔聲量數值計算和對比

由于穿孔板孔徑較小，結構網格較為密集，采用有限元法計算量較大且比較費時，因此采用間接邊界元法進行數值計算。仿真模型如圖4所示，利用12個平面波作為混響激勵聲源，定義障板模擬試驗環境的剛性墻面，在入射側定義邊界元網格屬性為透明單元，用于接收聲激勵，透射側邊界元網格與結構網格耦合，場點網格用于接收透射側的聲功率。將上述試驗測試的阻尼損耗因子和數值計算的傳遞導納導入到模型中去，進行計算，獲得穿孔板兩側的入射聲功率和透射聲功率，最后將入射和透射聲功率相除，就可以獲得穿孔板的隔聲量。仿真邊界條件的選取盡量接近實際狀態。

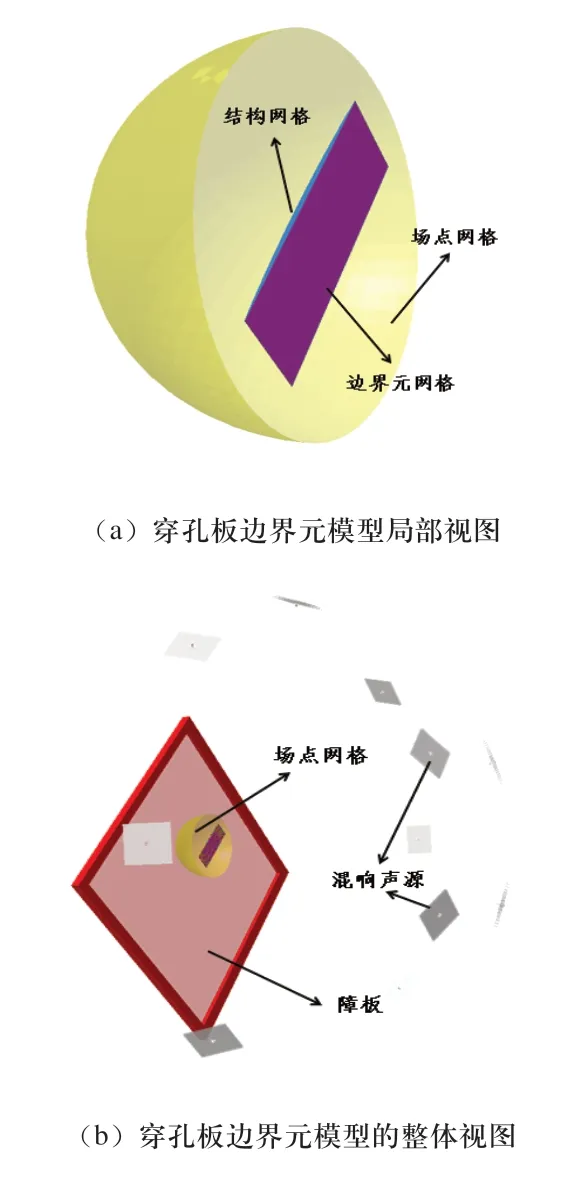
圖4 穿孔板的仿真模型

將使用邊界元方法計算的仿真隔聲量與試驗值進行比較，結果如圖5所示。

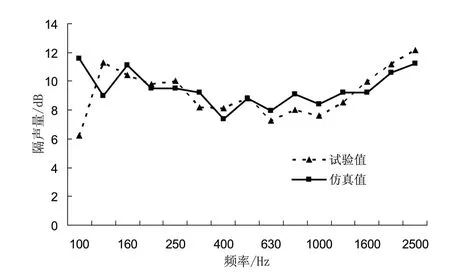
圖5 隔聲量的仿真與試驗比較

從圖5中可以看到，在160Hz以下的低頻范圍內，隔聲量試驗與仿真結果不僅在數值上相差比較大，變化趨勢也相反，主要因為該頻段內的隔聲性能主要由邊界條件確定，實際約束狀態比較復雜，使得仿真時很難準確地模擬，以至于結果相差比較大，超過160Hz，試驗與仿真在變化趨勢和數值上都很接近，總體而言，此種方法可以用來準確地預測穿孔板的隔聲性能。

5 聲輻射效率測試

結構振動所輻射的聲音是噪聲的主要來源之一。它通過結構振動，從而引起結構周圍流場的波動將能量傳播出去。

薄板結構在各個領域應用很廣泛。然而，由于其剛度較小，在工程應用中容易產生振動，從而輻射噪聲，成為噪聲源。因此，研究板件的聲輻射特性對于如何有效控制板件的結構形式、連接方式，從而改變結構的聲輻射特性，以獲得期望的結構的聲輻射特性就顯得非常重要而有意義了。

目前對聲輻射特性的研究主要基于聲強法，即通過結構輻射聲場的結構包絡面S上的聲強，通過聲強In與結構包絡面的乘積獲得結構的輻射聲功率∏，如式（8）所述：

但是，聲強法對測試環境很敏感，使得試驗往往只能在消聲室內進行，這樣成本較高，而且局限性很大。因此，對于工程實際的現場測量來說，聲強法并不能滿足測試要求。而且穿孔板上面存在很多小孔，使用傳統的聲振測試方法，會從小孔中漏聲，導致測試結果不準確，在此嘗試使用一種新的測試方法，即分離單元法。

對于活塞運動的聲輻射結構有：

如圖6所示，將板件離散成一系列矩形的振動單元，單元尺寸取決于研究的頻率范圍。將每一個振動單元視為一個小的振動活塞。通過求解每個單元的輻射聲功率，最終可以求得結構總的輻射聲功率。

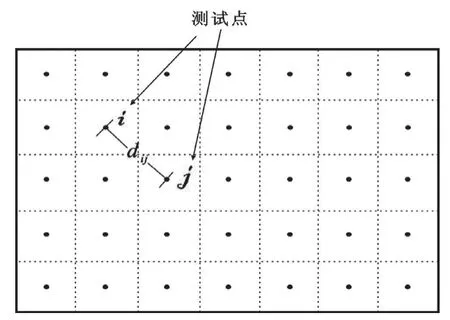
圖6 板件振動單元劃分示意圖

依據上述思想，將穿孔板劃分為14×15個單元，每次采用五個振動傳感器測量振動速度。

單元i的自輻射阻抗Rii為：

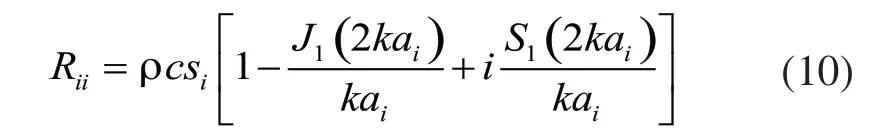
單元i和單元j之間的互輻射阻抗Rij為：

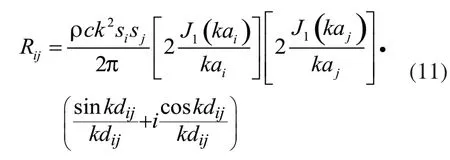
式中，ρ為空氣的密度，c為空氣中的聲速，Si和Sj為單元i和單元j的面積，J1為第一類一階Bessel函數，為空氣中的波數，為圓形單元等效為矩形單元的等效半徑，為虛數單位，S1為Struve function，dij為單元i和j的距離，如圖6所示。

根據單元的輻射阻抗可以求得單元i 的輻射聲功率∏i為：

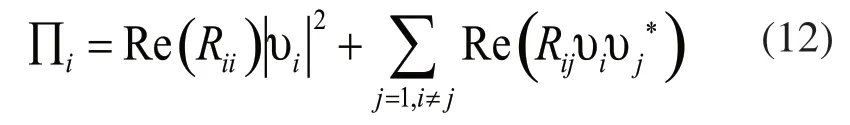
式中，Re表示取實部，υi為單元i表面的法向速度。*表示共軛復數。將所有單元的輻射聲功率求和即可求得板件的輻射聲功率。

由式（12）可見，只要測得單元表面的法向速度，即可方便地求得結構的輻射聲功率。由于只需測量結構的振動速度而不用測聲強或者聲壓，也不存在漏聲的狀況，所以該法具有更高的精度，而且也有更廣的適用性。

由于已經獲得結構表面的振動速度和輻射聲功率，因此不難獲得結構的輻射效率σ：

通過分離單元法測試的聲輻射效率如圖7所示。

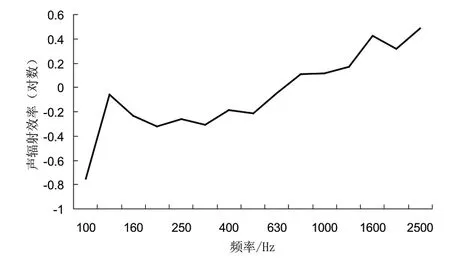
圖7 穿孔板的聲輻射效率

穿孔板的厚度只有1.5mm，致使其吻合頻率很高，圖中測試的頻率上限并未達到吻合頻率。聲輻射效率在吻合頻率以下，總體上會呈現出上升的趨勢，這與圖中的測試結果吻合，因此表明該種測試方法應用于穿孔板在一定程度上是可行的。

6 結束語

1)使用脈沖衰減法測試了穿孔板的阻尼損耗因子，數值上在0.15%～0.35%之間。為了獲得精確的有限元模型，計算了穿孔板兩側的傳遞導納。

2)將阻尼損耗因子和傳遞導納賦予穿孔板的邊界元模型，獲得隔聲量的仿真值，與試驗結果進行對比，總體趨勢上吻合良好，驗證此種仿真方法可以用來準確預測穿孔板的隔聲性能。

3)避開傳統聲振法在測試穿孔板聲輻射效率的不足，采用分離單元法進行測試，測試結果可靠，表明此種方法應用于穿孔板聲輻射效率的測試在一定程度上是可行的。

[1]盛勝我.穿孔板背面緊貼吸聲薄層時的聲學特性[J].聲學技術,2003,22(1):52-54.

[2]王占學,喬渭陽,李文蘭.微穿孔板消聲器在 MA60 飛機APU 排氣管的應用[J].航空動力學報,2003,18(3):331-335.

[3]馬大猷.微穿孔板吸聲結構的理論和設計[J].中國科學,1975,1(1):38-50.

[4]劉克.擴散場內微穿孔板吸聲特性的實驗研究[J].聲學學報,2000,25(3):211-218.

[5]李民,舒歌群,梁興雨.4100QB 柴油機齒輪室蓋聲輻射效率試驗研究[J].農業工程學報,2011(12):148-152.

[6]Bolduc M,Atalla N.Measurement of SEA damping loss factor for complex structures[J].The Journal of the Acoustical Society of America,2008,123(5):3060-3060.

[7]張紅亮,孔憲仁,劉源,等.寬頻域的內損耗因子實驗辨識方法研究[J].振動與沖擊,2013,32(12):179-184.

[8]陳馨蕊,楊陳.鎂合金 AZ31 阻尼性能的實驗研究[J].浙江大學學報:工學版,2010(1):19-22.

[9]康鐘緒,季振林.穿孔板的聲學厚度修正[J].聲學學報,2009,33(4):327-333.