定位坐標分量依賴于衛星高度角的靈敏度分析

岳 俊，何 冰

(1.北京大學地球與空間科學學院，北京100871;2.武漢大學測繪學院，湖北武漢430079)

一、引 言

在GPS外業測量中，經常會遇到遮擋導致高度角變大的情況，影響測量精度，要減小高度角通常要付出一定成本。本文通過大量統計分析出對測量精度影響最大的截止高度角，測量時使遮擋產生的高度角小于此截止高度角通常會得到較大的效益。本文的結果將為GPS外業觀測計劃的制訂提供參考。

DOP值通常到了一定高度角就會產生顯著變化，但僅通過DOP值的數值變化并不能正常反映其依賴于衛星截止高度角的靈敏度。本文提出了GPS不可用率并用其衡量DOP值的變化，對GPS不可用率進行小波濾噪和曲線擬合，求出其對應的分布函數和概率密度函數，以此計算各個DOP值的靈敏度。同時本文通過大量的數據處理，建立了5種DOP值之間的統計經驗模型。

二、DOP值依賴于衛星截止高度角的變化規律

獲得高精度定位結果的重要因素是可視衛星擁有良好的幾何圖形結構，尤其是對單點定位和定態測量而言。可見性是指衛星和接收機之間的通視。由于衛星和用戶間存在相對運動，衛星的空間幾何圖形結構會隨時間而變化。瞬時衛星幾何圖形一般采用精度衰減因子(dilution of precision，DOP)進行評定［1］。

由于DOP值的計算依賴于衛星高度角，當截止衛星高度角變化時，可見衛星數和DOP值隨之發生變化，DOP值在單歷元依賴于衛星高度角的變化情況如圖1所示。

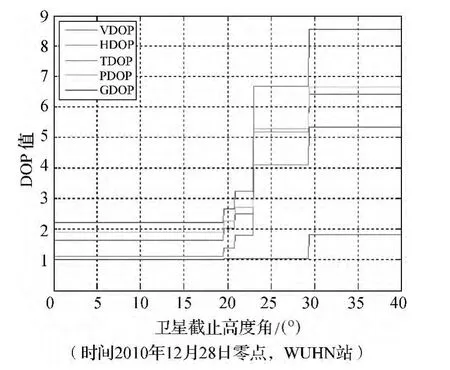
圖1 單歷元DOP值隨衛星截止高度角的變化

由圖1及DOP值計算方法可知，只有截止高度角處存在，衛星DOP才會發生變化，因此對于單歷元，截止高度角-DOP值二維圖為階越型。為了得到DOP值隨著高度角變化的統計規律，對單天96個歷元的DOP值按角度取平均，得到圖2。

由圖2可以分析出，由于DOP值的計算方法，DOP值會隨著衛星截止高度角的增大而顯著增大，如果直接對DOP值進行擬合，將難以得出符合實際的定位坐標分量精度依賴于衛星高度角的靈敏度，因此本文擬從統計學的角度得出衛星高度角的靈敏度。對此，本文提出“GPS不可用率”這個概念。

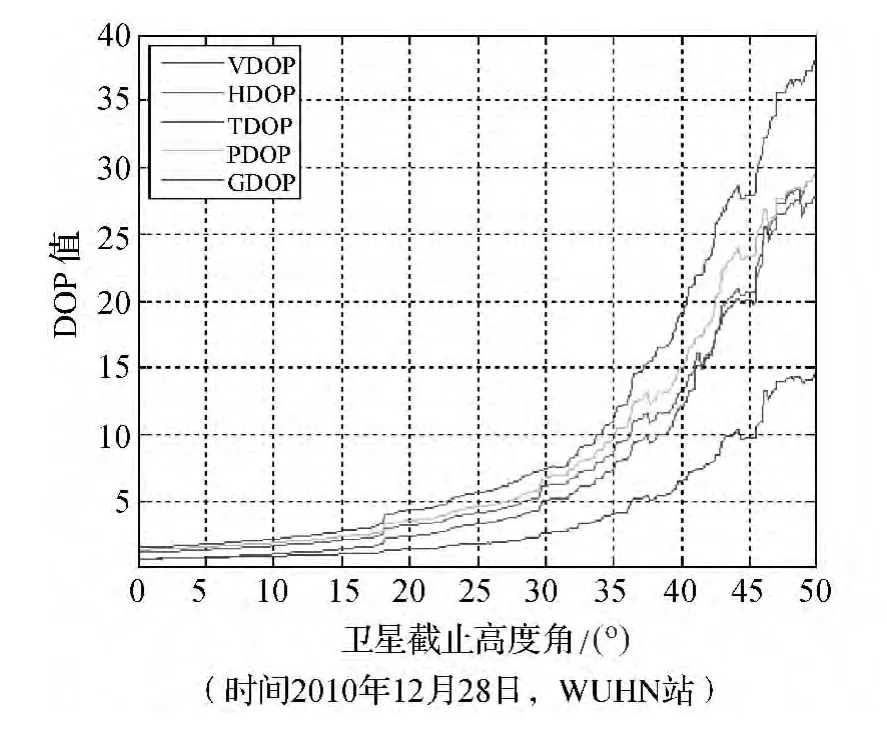
圖2 96歷元平均DOP值隨衛星截止高度角的變化

GPS衛星可用性是指GPS系統的服務可以使用的時間的百分比，由文獻［2］分析得知，GPS可用性將取決于精度要求的嚴格程度，其分析認為PDOP≤6為GPS可用性的門限。由此可得，對于單歷元必有唯一一個門限高度角。對于多個歷元，每一個高度角均對應一個GPS可用歷元數，將GPS可用歷元數除以總歷元數定義為GPS可用率，將歷元數減GPS可用歷元數除以總歷元數定義為GPS不可用率。

GPS不可用率隨著衛星高度角的增加而增大，最小值為0，最大值為1。GPS不可用率越高，表明定位精度越低。從中可以找到GPS衛星可用率隨著衛星截止高度角變化的靈敏度，并計算靈敏度最大值，在全球范圍內得出靈敏度的置信區間。

由于文獻［2］僅給出了 GPS可用性選擇的PDOP門限值，對10周數據進行建模，構建VDOP、HDOP、TDOP、GDOP與 PDOP的經驗關系，以此求出 GPS 可用性選擇的 VDOP、HDOP、TDOP、GDOP門限值。

取截止高度角為40°，對10周共70天6720個歷元的數據進行DOP值數據擬合。數據擬合如圖3所示。

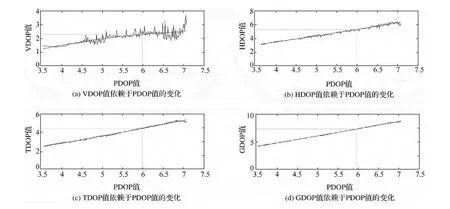
圖3 DOP值數據擬合

由DOP值擬合曲線方程可以得知，PDOP值為6 時，HDOP、VDOP、TDOP、GDOP 分別為 2.394 5、5.492 7、4.601 1、7.561 4，滿足 DOP 值的基本關系方程。將這些值分別取為門限DOP值，由5個門限DOP值對應的門限高度角所計算出來的GPS不可用率隨衛星的變化如圖4所示。

由圖4可得，通過取5種DOP值的門限值計算出來的GPS不可用率幾乎相同，證明GPS不可用率的概念有其重要的價值，在單個DOP值計算中，如果截止高度角內的衛星數小于4則無法計算出來，通過計算GPS不可用率這個統計值可以得到GPS定位精度隨著高度角的變化值。

三、基于小波濾波和曲線擬合的靈敏度計算

在得到DOP值概率分布離散形式后，由于數據處理過程的不完善等因素，必然會存在高頻的噪聲，因此需要對采集到的離散的概率分布函數進行濾波降噪。本文中采用小波變換的方式進行去噪處理。

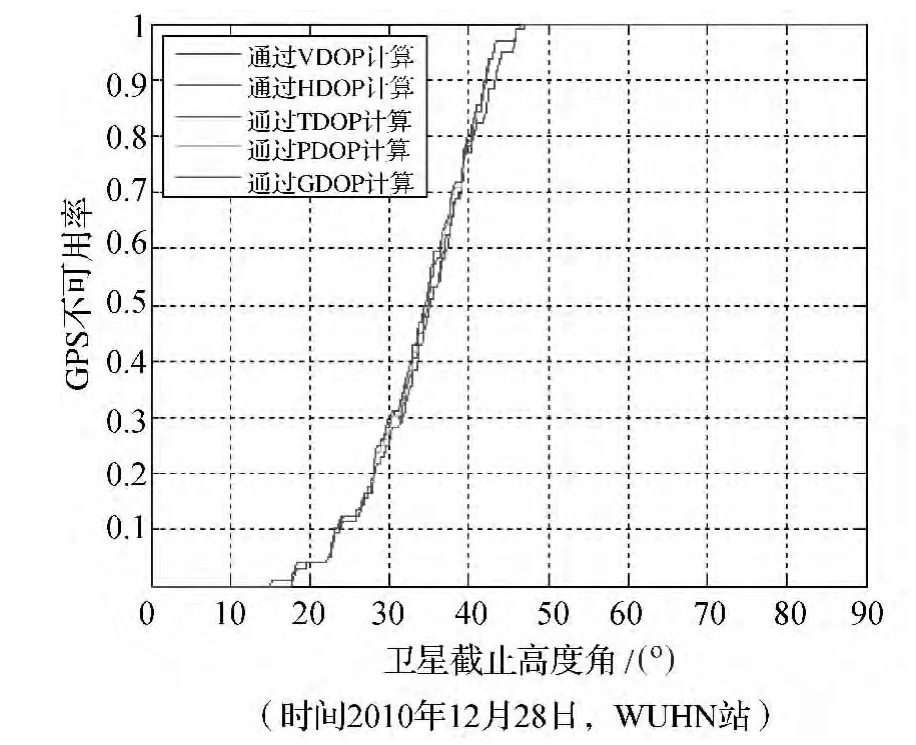
圖4 5種DOP值計算得出的GPS衛星不可用率隨衛星截止高度角的變化

在小波分析中，尺度函數φ(x)表示低頻整體部分，小波函數ψ(x)表示高頻細節部分，通常采用塔式Mallat算法進行小波分解和重構。設有離散信號，將其加載到尺度函數上得到，則 有 如 下 Mallat 算 法 卷 積 表達式［3］

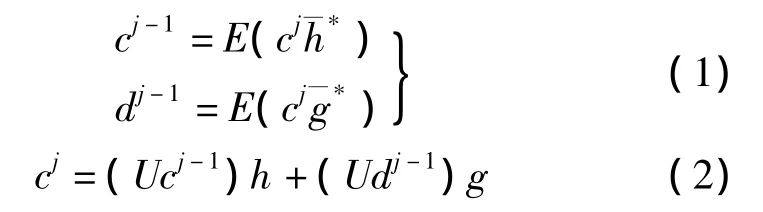
式1表示小波分解，式2表示小波重構。式中，cj-1表示分辨率2j-1上的近似信息;dj-1表示位于分辨率2j-1～2j之間的細節信息。

設長度為N的信號fn被噪聲en污染，所測得的含噪數據為xn=fn+en。對含噪數據用Mallat算法進行分解，得到低頻的整體部分和高頻的小波部分［4］。對高頻部分做閾值處理，閥值為

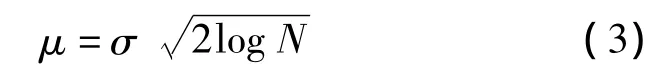
式中，μ為閾值;σ為估計的噪聲標準差。

分解與重構結果如圖5、圖6所示(以GDOP為例)。

在經過小波變換后，由于衛星分布的不連續性等因素的影響，離散點陣的簡單勾連所得到的曲線其變化仍然不是特別平滑，故需要對其進行擬合。根據上述小波重構得到的未擬合的概率分布函數可知，其在0—15°范圍內不可用率為0，在50°以后不可用率累計保持為1。故在選擇最優的擬合函數的時候除了需要考慮擬合函數與原函數殘差較小外，還需要保證擬合函數的微分函數在0—15°和50°以上函數值近似等于0。根據上述條件，結合實際觀測數據確定采用23階多項式模型擬合該概率分布函數為最佳。擬合后的概率分布函數及其概率密度函數如圖7、圖8所示。

圖5 小波分解

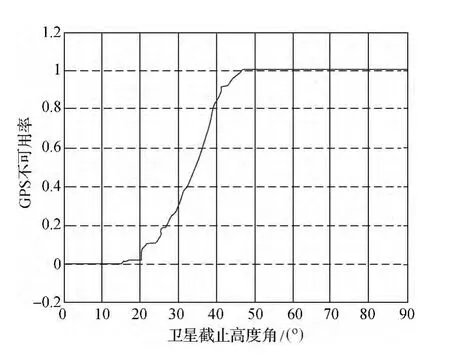
圖6 一維小波重構

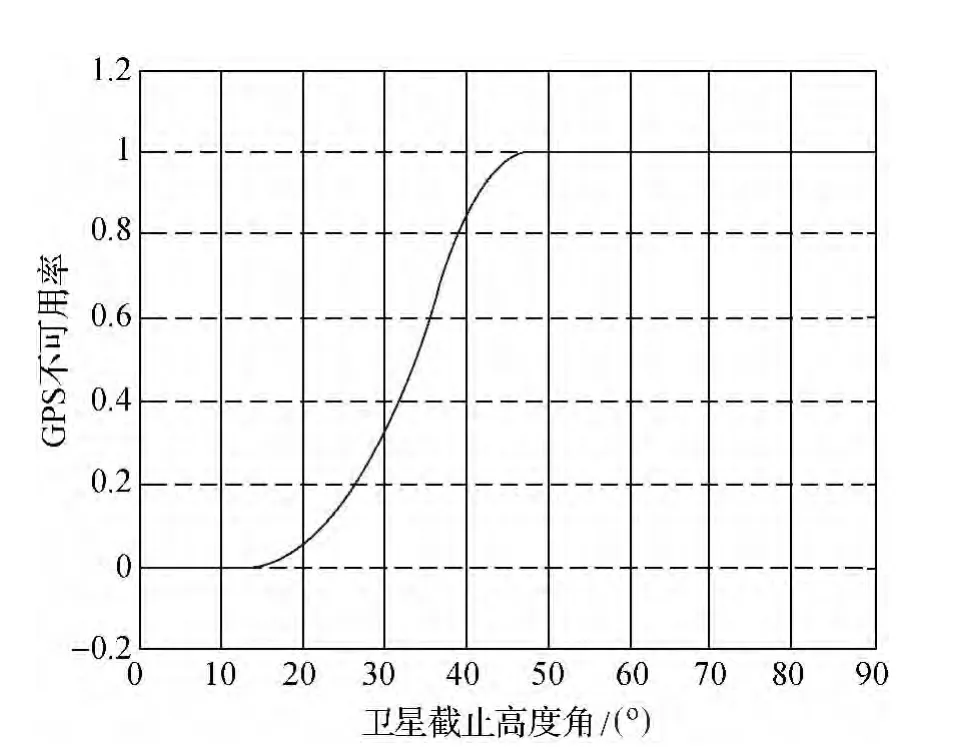
圖7 擬合后的概率分布函數

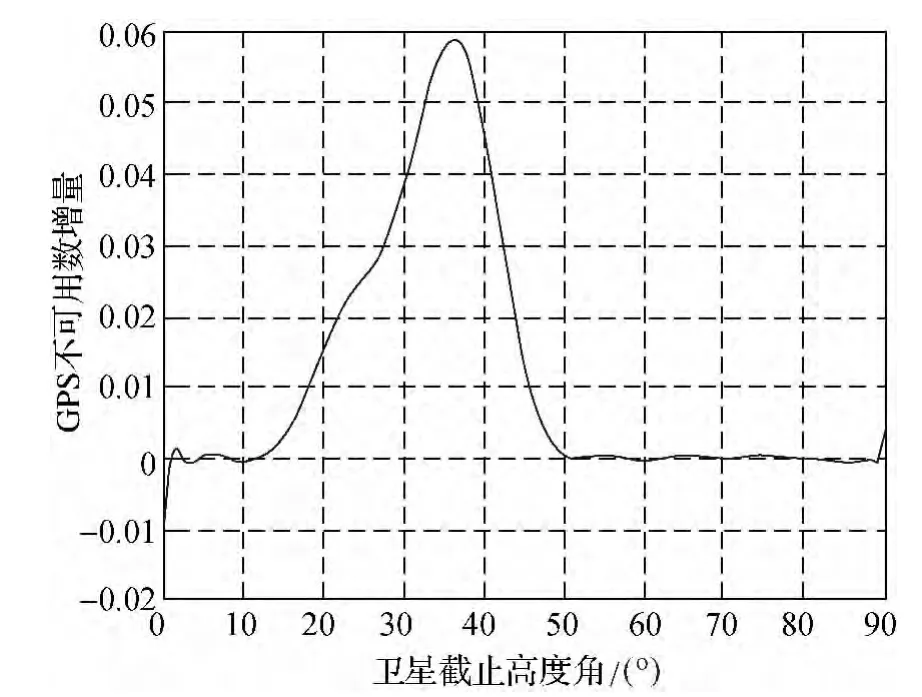
圖8 概率密度函數

四、基于DOP值概率分布函數和概率密度函數的靈敏度分析

所謂靈敏度是指定位坐標分量的精度隨著衛星高度角變化的變化率。而對定位坐標分量的精度進行衡量的指標即為各類值，故靈敏度可以理解為各類DOP值相對于角度變化量的變化率。如前所述DOP值在不加限制條件的情況下，其值隨角度的增大而加速增大，以此計算出來的靈敏度也必將隨著角度增加而增大，在90°時達到最大。但是這并沒有現實的意義，因為一般高度角大于50°時即無法進行實際觀測。所以本文設定了DOP值的閾值，并以此為基礎統計不同高度角時DOP值超過閾值的百分比，即衛星的不可用率。然后通過研究衛星的不可用率隨角度變化的概率分布函數及其概率密度函數，來間接確定衛星靈敏度隨角度變化的規律。

根據上述在WUHN站以GDOP值計算所構建的擬合后的概率分布函數圖像和概率密度函數可知:衛星在0—15°范圍內全部可用，在50°以上完全不可用，故靈敏度均為0，對應的概率密度函數在該范圍內也應趨近于0。在15—50°的范圍內根據概率分布函數可知，衛星的不可用率顯著增加，并在50°附近達到100%，根據概率密度函數可知衛星不可用率的增長率先增大后減小，在36.5°附近達到最大，故可認為GDOP值所對應的靈敏度在15°—50°的范圍內先增大后減小，在36.5°附近最大。

通過上述分析可知在15°左右時開始出現不可用衛星，在36.5°左右定位坐標的整體精度(對應GDOP值)依賴于衛星高度角的靈敏度達到最大。所以在實際的工程應用中可以根據實際的觀測條件和精度要求，設定不同的衛星高度角。根據上述結論，在要求整體精度最優的情況下，如果受到條件的限制而不能以0—15°范圍內的高度角進行觀測，接收機觀測的截止高度角最大不應超過36.5°。

對全球8個IGS站應用上述模型，求出8個測站DOP值靈敏度最大值對應高度角，其結果見表1。

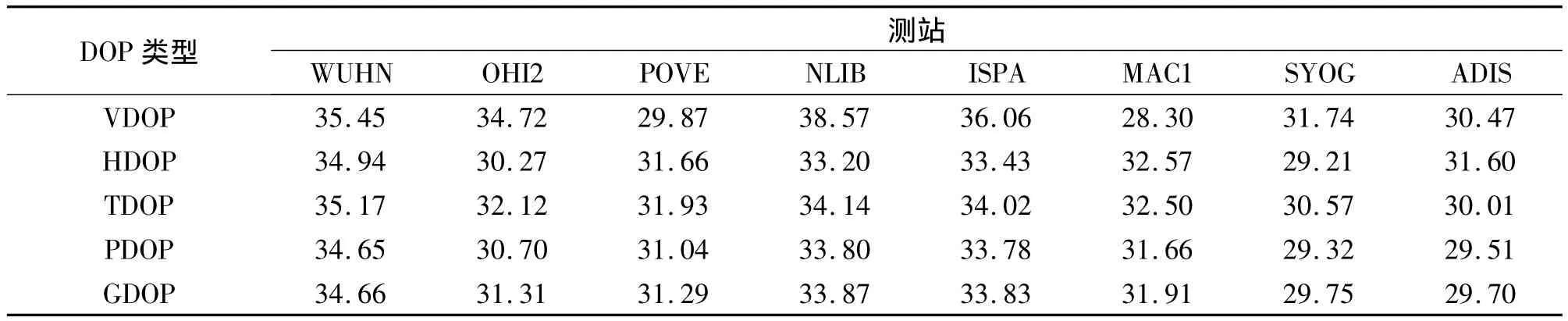
表1 全球多個測站的靈敏度最大值對應高度角(°)

由表1可知，各個站所定位坐標分量靈敏度最大值所對應的高度角有一定區別，但是基本上在30°以上。通過本文所建立的模型，輸入測站對應的坐標即可計算出其靈敏度最大的高度角。在GPS外業測量時，如果衛星截止高度角高于30°，則測量誤差會顯著增大。測量時遇到遮擋應盡量使遮擋后產生的高度角低于30°，將會獲得比較大的效益。

五、結束語

本文主要進行了定位坐標分量依賴于衛星高度角的靈敏度分析，提出了全角度區間衡量DOP值的統計的指標“GPS不可用率”，建立了5種DOP值之間的經驗關系模型，并通過小波濾波、曲線擬合等方法成功獲得GPS不可用率隨截止高度角的變化及其概率密度函數，以此獲得了定位精度靈敏度最大時所對應的截止高度角，并提出了GPS觀測時的注意事項，可為GPS外業觀測計劃的制訂提供參考。同時對比了多個IGS站應用該模型的結果，可知影響模型結果的因素與測站地理位置、衛星軌道整體布局的相對位置有關，這將作為后續研究的重點。

［1］HOFMANN W，LICHTENEGGER，WASLE.GNSS——Global Navigation Satellite Systems GPS，GLONASS，Galileo， and More［M］. Berlin:Springer， 2007:262-266.

［2］ELLIOTT D K，CHRISTOPHER J H，HEGARTY C J.Understanding GPS:Principles and Applications［M］.2nd Ed.Norwood:Artech House，Inc，2005:334-343.

［3］MALLAT S G.A Theory for Multiresolution Signal Decomposition:the Wavelet Models［J］.IEEE Trans on A-coustics，Speech and Signal Processing， 1987，37:2091-2110.

［4］李振，朱鋒，陳家君.基于小波變換的橋梁風振變形監測數據處理［J］.測繪通報，2011(11):18-20.

［5］成禮智，王紅霞，羅永.小波的理論與應用［M］.北京:科學出版社，2004:67-68.

［6］黃聲享，劉經南，柳響林.小波分析在高層建筑動態監測中的應用［J］.測繪學報，2003，32(2):104-107.

［7］LANGLEY R B.Dilution of Precision［J］.GPS World，1999，10(5):52-59.

［8］SHARP I，KEGEN Y，GUOY J.GDOPAnalysis for Positioning System Design［J］.IEEE Transactions on Vehicular Technology，2009，58(7):3371-3382.

［9］SRILATHA，G.SASI B R，S.Swapna R，et al.Investigation of GDOP for Precise User Position Computation with All Satellites in View and Optimum Four Satellite Configurations［J］.The Journal of Indian Geophysical U-nion，2009，13(3):139-148.

［10］王澤民，孟泱，伍岳，等.GPS、Galileo及其組合系統導航定位的DOP值分析［J］.武漢大學學報:信息科學版，2006，31(1):9-11.