儲層巖石物理參數對地震參數的影響分析
肖風凱 王茂均 粟亮 曾銘 劉悅
(成都理工大學,四川成都 610059)
儲層巖石物理參數對地震參數的影響分析
肖風凱 王茂均 粟亮 曾銘 劉悅
(成都理工大學,四川成都 610059)
儲層流體研究對于地震勘探有著十分重要的意義。本文利用經典的Boit- Gassmann方程, 在孔隙度不同的條件下, 通過對目的層進行不同成分的流體替代, 研究了孔隙度、飽和度以及流體成分等巖石物理參數對等效巖石的縱橫波速度、密度等地震參數的影響, 并對計算結果的變化規律進行分析。正研究結果表明:含氣飽和度的變化使混合流體的可壓縮性發生改變, P波速度隨含氣飽和度的增加先急劇下降,而后轉為緩慢升高;孔隙度的變化對P波速度、S波速度和介質密度的影響要大于含油、含氣飽和度變化的影響;當目標層充填的流體由氣變為油、水時, 目標層的地震響應的AVO 現象變得不明顯, 并且隨著目標層厚度的逐漸減少, 地震響應產生調諧效應。
Gassmann方程 流體置換 AVO正演 飽和度 孔隙度 薄層 調諧效應
1 儲層地質模型
假設地質模型為三個水平層狀介質。選擇第二層為目標層,進行流體替代, 利用計算結果對縱橫波速度、密度的變化規律進行分析。然后改變目標層的厚度和流體成分, 正演合成地震記錄, 分析流體以及厚度對AVO 地震響應的影響。
1.1 地層模型參數
第一層為800m厚層泥巖,層參數:

圖2
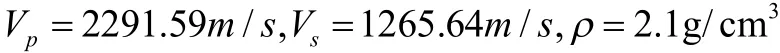
第二層為目標層(流體替換層)為薄層砂巖;
第三層為半無限泥巖空間,層參數:
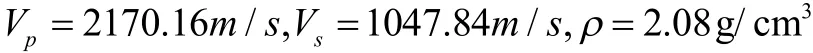
1.2 孔隙流體參數
水、油、氣三種流體進行流體替代,水的密度為1.0g/cm3,體積模量為2.2GPa;氣的密度為0.14g/cm3,體積模量為0.02GPa;油的密度為0.8g/cm3,體積模量為1.0GPa。
2 流體置換的理論基礎--Gassmann方程
Gassmann方程是巖石彈性物理研究的重要理論工具,它建立了巖石物性參數與地震彈性參數進行溝通的橋梁,并為進一步利用地震信息劃分巖性、檢測油氣提供了理論依據。
Gassmann方程的假設:(1)巖石(基質和骨架)宏觀上是均勻、各向同性、完全彈性的;(2)所有孔隙都是連通的;(3)孔隙內部充滿無摩擦的流體(液體、氣體和混合物);(4)巖石—流體是封閉系統(不排液);(5)當巖石被地震波激勵時,流體和骨架之間沒有相對運動;(6)孔隙流體對骨架無軟化或硬化作用。
在均勻各向同性介質中,流體飽和的多孔介質的縱波速度 vp
和橫波速度 vs可以寫成:
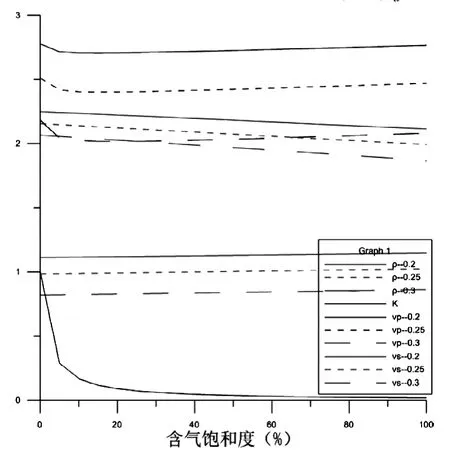
圖3

圖4 充填不同流體對頂、底界面反射系數的影響
在已知巖石礦物成分和孔隙流體的組成的情況下,本文目標層砂巖的基本參數設為:μm—巖石基質剪切模量,GPa;
采用Nur等人1991年提出的經驗公式估算 Kd, μd;為砂巖的臨孔隙度值為0.4;
混合流體體積模量 Kf可以用WOOD方程:
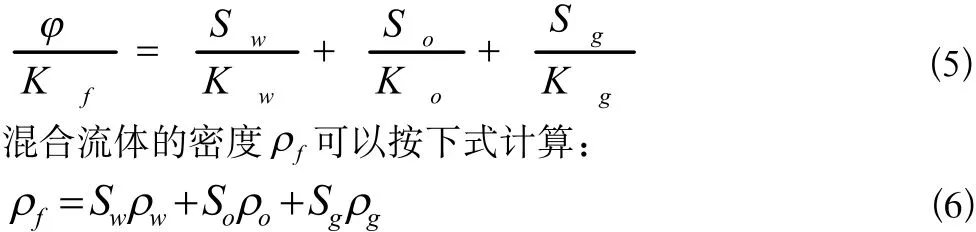
3 流體置換模擬結果分析
3.1 流體成分、孔隙度和飽和度對地震參數的影響
選定第二層為目標層,根據Biot-Gassmann理論,對它進行流體替代, 建立水-氣,水-油,油-氣混合流體替代模型分析儲層孔隙度、流體飽和度變化對縱橫波速度,以及等效介質密度的影響情況。假設替代層的孔隙度分別為φ=20%,25%,30%,水的密度為1.0g/cm3,體積模量為2.2GPa;氣的密度為0.14g/cm3,體積模量為0.02GPa;油的密度為0.8g/cm3,體積模量為1.0GPa[2]。如圖1、2、3。
不含氣的情況下,圖1中含油飽和度從0~100%,縱波速度平滑遞減,從三種孔隙度縱波速度曲線可以看出巖石孔隙度越小速度越大,這與實際情況相符,孔隙度越小,巖石越“實”,縱波速度越大;混合流體體積模量隨含油飽和度的增加遞減,這是由于油的體積模量小于水的體積模量,當含油飽和度增加時混合流體的體積彈性模量減小;混合流體密度平滑遞減。
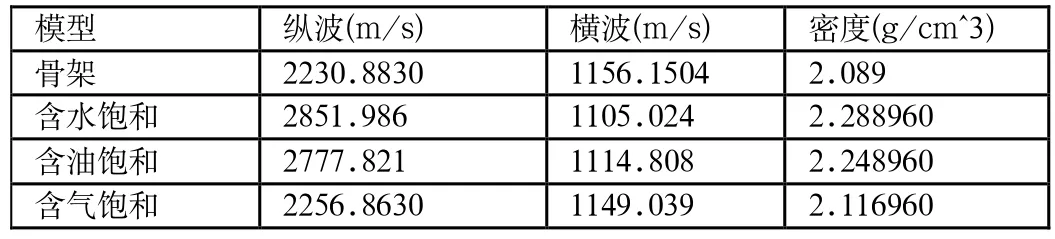
表1 流體替代參數表
在不含油的情況下,圖2中含氣飽和度從0~100%,縱波速度先陡然下降,然后再平滑緩慢上升,上升幅度很小,從三種孔隙度縱波速度曲線可以看出巖石孔隙度越小速度越大;混合流體體積模量在流體中含有氣體的時候陡然從2.2下降到0.35,然后再隨含氣飽和度的增加緩慢下降;混合流體密度隨含氣飽和度增加遞減,其遞減幅度略大于混合流體體積模量。
在不含水的情況下,圖3中含氣飽和度從0~100%,縱波速度先陡然下降,下降幅度比水—氣模型小,然后再平滑緩慢上升,上升幅度很小,從三種孔隙度縱波曲線可以看出巖石孔隙度越小速度越大;混合流體體積模量在流體中含有氣體的時候陡然從1下降到0.35,然后再隨含氣飽和度的緩慢下降;混合流體密度遞減,其遞減幅度略大于混合流體體積模量。
結論:①一般認為流體內沒有剪切波,流體的孔隙度和飽和度的變化對橫波的影響不是很大,所以流體只是通過密度的變化影響橫波速度。②同時流體中含氣對等效介質的縱波速度影響很大。③但是隨著含氣飽和度的逐漸增加, 等效介質的縱波速度變化不大。所以,只能確定混合流體相中含氣體,但不能確定含氣量。因此,地層充填水氣混合流體和油氣混合流體時的等效速度都和地層完全飽含氣時的等效速度相當,在AVO地震響應上差別不明顯。
3.2 流體和地層厚度對地震響應的影響
3.2.1 AVO技術基礎
本文中采用依賴于角度的Zoeppritz線性近似常規方程:(7)式中:
α、β、ρ分別為上下層的平均速度、密度;Δα、Δβ、Δρ 分別為上下層速度、密度差。
3.2.2 流體置換模型
下面討論的模型都是在目標層孔隙度為20%的情況下進行的。表1是目標層含水、含油、含氣飽和度分別為100%時,計算出來的等效介質的縱橫波速度、密度(如表1)。
圖4—a中,目的層飽含油砂巖以及飽含水的砂巖聲阻抗大于圍巖的阻抗,隨著入射角的增加反射振幅逐漸增強;飽含氣的砂巖以及干骨架的砂巖,振幅隨入射角的增加先減小后增大,在入射角為20時出現極性反轉現象[4];
圖4—b中,目的層飽含油砂巖以及飽含水的砂巖聲阻抗小于圍巖的阻抗,那么隨著入射角的增加反射振幅逐漸增強。
為了更加全面的觀測流體和厚度對地震響應的影響,利用表1中的模型數據,對目標層進行流體替代,選用35Hz的雷克子波,采樣間隔為0.002s,合成地震記錄。為了觀測薄層AVO現象,正演模擬中改變目標層的厚度,合成地震記錄。
由合成記錄可知,目標層在含氣和含油的情況下,地震記錄很相似, 但是含油時地震反射比含水時的低;目標層含氣時,隨著目標層厚度的減少,地震記錄出現反向;并且目的層含水時的底界面的反射時間比含油和含氣時底界面的反射時間提前,這是由于氣、油、水三種流體的體積模量是逐漸增加的,從而引起砂巖速度的增加,使得地震波傳播時間超前。分別對比充填不同流體時厚度對地震響應的影響:隨著厚度的減少,地震響應產生調諧效應,當地層厚度小于地震分辨率時,反射振幅與厚度有關,即其頂和底的反射會產生干涉疊加效應。由于目標層飽含水和飽含油的等效速度大于上下層界面的速度,所以在目標層的上下界面形成反極性反射,隨著目標層厚度的減少,頂界面的反射振幅先增加后減少,并且當目標層的厚度小于地震分辨率時,地層厚度與反射振幅成近似的比例關系;當目標層飽含氣時,目標層的上下界面形成同極性反射,隨著地層厚度的減少頂界面反射振幅增加。
4 結語
基于薄儲層地震反射模型,應用Gassmann流體置換方程分析了薄砂巖儲層流體飽和度和孔隙度變化對砂巖物性參數的影響;通過AVO正演模擬技術,分析厚度與流體對AVO地震響應的影響,總結出不同流體飽和情況下的地震響應特征,建立巖石流體性質和地震響應特征的聯系,這是進行AVO分析的基礎。得到以下認識:(1)P波速度隨含油飽和度的增加而降低,對含氣飽和度的增加先急劇降低后緩慢增加;S波速度隨含油和含氣飽和度的增加呈線性增加趨勢;介質密度隨含油和含氣飽和度的增加線性降低;P波速度、S波速度和介質密度隨孔隙度的增加線性降低,降低程度大于隨流體飽和度變化時的情形。(2)目標層在飽含水和飽含油的情況下,PP波的反射系數變化相似,在0到59范圍內,反射振幅都隨著入射角的增大而增大,但是含油時地震反射比含水時的低。同樣目標層在飽含氣與干骨架的情況下,PP波的反射系數變化相似,都出現了極性反轉現象。(3)當目標層充填的流體由氣變油和水時,目標層的地震響應的AVO現象變得不明顯,并且隨著目標層厚度的逐漸減少,地震響應產生調諧效應。
[1]陳信平,劉素紅.淺談Gassmann方程[J].中國海上油氣,1996,11(2):122~127.
[2]劉亞茹.儲層流體特征及AVO地震響應分析[J].中國西部油氣地質,2007,11:85~89.
[3]傅戈平.多屬性AVO分析及疊前參數反演方法研究.成都理工大學畢業設計論文.
[4]林凱,賀振華,熊曉軍,黃德濟.基于Gassmann方程的流體替換流程[J].長江大學學報自然科學版,2009,6(1):180~181amp;205.
[5]林凱,鐘結麟,賀振華,熊曉軍.基于Gassmann方程巖石速度倒轉現象成因分析.成都理工大學油氣藏地質及開發工程國家重點實驗室.
注:肖風凱、王茂均 為共同第一作者。

