基于馬爾可夫鏈的自適應性神經網絡訓練算法*

莫紅枝

（玉林師范學院 教育技術中心，廣西 玉林 537000）

0 引言

神經網絡算法是一種非線性計算模型，近年來成為模式識別中常用的工具之一。在多層神經網絡中，系統的性能不僅受到隱含層數、隱含層神經元數量的影響，而且還與激勵函數的選取和訓練算法直接相關。

在目前的研究中，采用最為廣泛的為S型激勵函數[1-2]，S型函數容易減慢網絡的收斂速度，甚至可能導致陷入局部最小值[3]。針對這一問題，近幾年采用自適應激勵函數對神經元輸入的加權和進行計算已經成為一種趨勢，并應用于股票預測[4]、文字識別[5]等方面。本文針對常見的S型函數,改進了自適應性激勵函數神經網絡系統框架，提出基于馬爾可夫鏈的學習算法，并將其應用到故障診斷領域，取得了比較好的實驗結果。

1 自適應性神經網絡

1.1 多層神經網絡

多層神經網絡一般包括一個輸入層、一個輸出層、一個或者多個隱藏層。隱藏層每一層網絡中都包含多個神經元，對每個神經元的輸入都是由上一層輸出的加權和，例如對于第n組樣本數據，第k層上的第j個神經元的輸入可以通過計算上一層的加權和來計算，計算公式為：

其中，wkji表示上一層網絡中的第i個神經元對于第k層上的第j個神經元之間的權重值。yki(n)表示第 k層網絡上第i個神經元的輸出值。當k=1時，表示該層為輸入層，其輸出值就是對于整個神經網絡的輸入值，即y1i(n)=xi(n)，神經元的輸出由輸入經過激勵函數計算得到，即：

其中，φkj表示第k層第j個神經元的激勵函數。為了增加神經網絡算法的非線性映射能力，隱含層的激勵函數可以選取非線性函數，常見的包括雙正切函數和S型函數。輸出層上神經元的輸出就是整個神經網絡系統的輸出。為了獲得最優的權重值，需要對神經網絡進行訓練。在給定訓練樣本后，對神經網絡進行訓練過程的實質是不斷調整權重值，使神經網絡計算的輸出值與理論上的輸出值之間的誤差最小，即：

其中，din和 yin分別為第i個神經元上真實情況下的輸出值和實際計算結果的輸出值，N為訓練樣本的個數。

1.2 激勵函數

本文以傳統的三層神經網絡結構，設計出基于改進的S函數的自適應性神經網絡。其特點在于隱含層的激勵函數不再是固定的函數，而是包含了可變參數的激勵函數，這種神經網絡系統框架如圖1所示。其中輸入層的神經元數量由選取的特征的個數決定(1，2，…，N)，輸出層神經元個數為 4 個（S1，S2，S3，S4），隱含層神經元的輸入是輸入層各個神經元輸出的加權和，并采用了自適應性的激勵函數對隱含層的輸入進行計算(I1，I2…Ik)。計算結果通過加權求和作為輸出層的輸入。在輸入層并未采用任何激勵函數，輸出層采用經典的S型激勵函數，如：

式（4）由S型函數演化而來，是一種常用的自適應性激勵函數，式中的α和β為可變參數。雖然該函數已經應用到神經網絡算法中，卻很少有文獻將其應用在解決機械設備故障分類問題中。

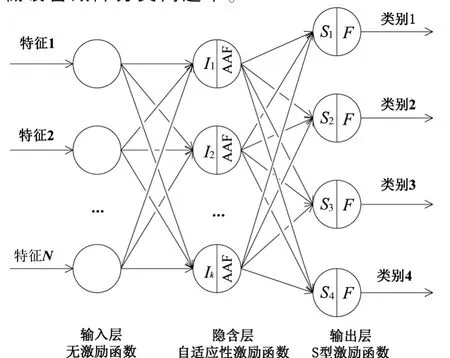
圖1 多層神經網絡算法系統架構

2 基于馬爾可夫鏈的訓練算法

2.1 算法描述

樣本訓練即是在給定一定數量的樣本時，利用式(3)對所有的權重進行最優化估計的過程[6-7]。當樣本數據中含有噪聲時，會造成程序魯棒性很差，給傳統的訓練方法帶來困難，本文假設式(3)中的誤差服從于高斯分布，然后根據后驗概率構造出馬爾可夫鏈，完成對權重的訓練，可以有效避免噪聲對訓練結果造成的影響，具有收斂速度快的優勢。假設樣本中含有噪聲，因此實際輸出與理想輸出之間的關系為：

式(5)的含義是對權重和自適應性參數進行估計，首先建立出的最大似然估計為：

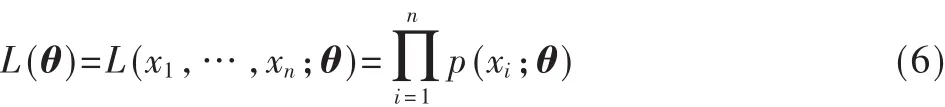
其中 θ={w，α，β}為要估計的參數向量，xi為第 i個含噪樣本。根據Hammersley-Clifford理論，在給定樣本X時，利用條件分布 pi(θi|θ{j≠i}，X，E)可以從聯合分布 p(θ|X，E)中產生足夠的點，趨近使得誤差E最小的最小二乘估計值。因此本文通過條件分布不斷調整權重和可變參數的值，使其得到訓練：

假設樣本數據中的噪聲符合正態分布，則：

因此：

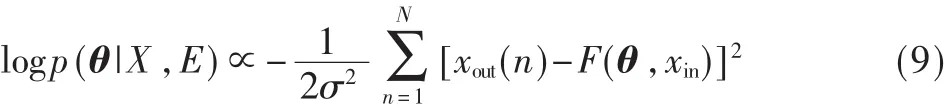
在得到θ的條件分布后，則各個權重及可變參數可以通過以下的算法進行更新。

算法一：

輸入：樣本 X，迭代次數 I，初始值 θ(0)={w0，α0，β0}

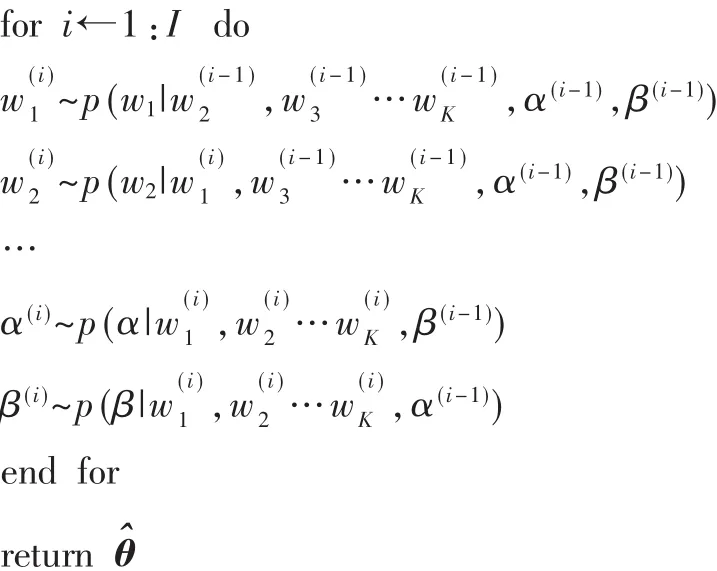
從上面算法可以看到，通過不斷對各個參數進行更新，形成了馬爾可夫鏈，最終可以得到最小二乘估計。

2.2 參數分析

下面以式（4）為例給出條件分布的計算公式：

（1）對于權重 wk

求取其分布時只需要將其他變量看作固定值，則可以得到其分布：

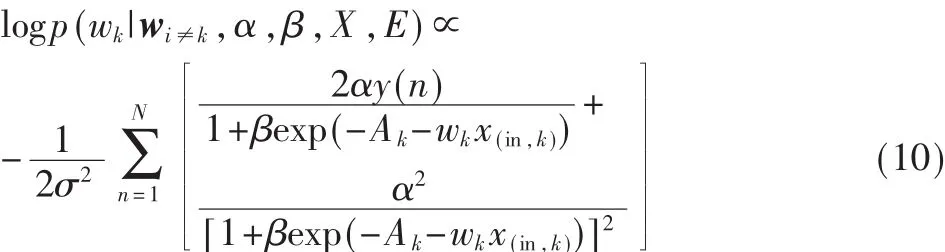
算法二：

第二步：u～U(0，1)

第三步：wk～(wk)

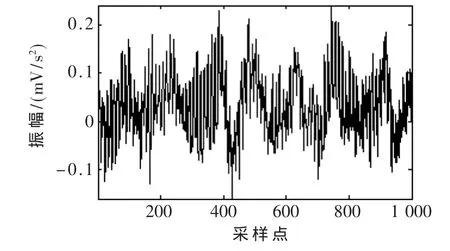
圖2 正常軸承振動信號

（2）對于參數 α

通過簡單的推導可以得出參數α的條件分布仍然服從于正態分布：

（3）對于參數 β

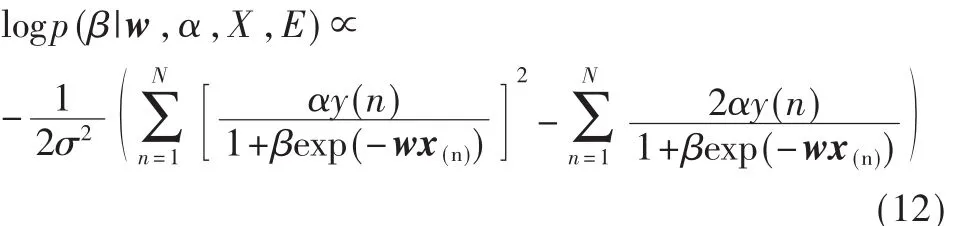
式（12）中的概率也是很難處理的，為簡化程序，同樣采用拒絕性采樣算法對β進行更新。

3 實驗結果仿真

3.1 數據準備

為對神經網絡性能進行驗證，利用本文設計的自適應性神經網絡設計出了分類器，應用于軸承故障診斷當中。選取的樣本數據來自于美國凱斯西儲大學股東軸承數據中心。軸承型號為SKF公司的6205-2RS型的深溝球軸承。考慮了4種軸承故障，分別為內圈單點故障、外圈點蝕及滾動體點蝕和正常工作信號。4種信號的波形分別如圖2～圖5所示。

訓練樣本空間總共選取了1 136個個體，每個個體包含512個采樣點。通過小波分解提取出了20個小波系數作為分類器的輸入。

3.2 訓練結果

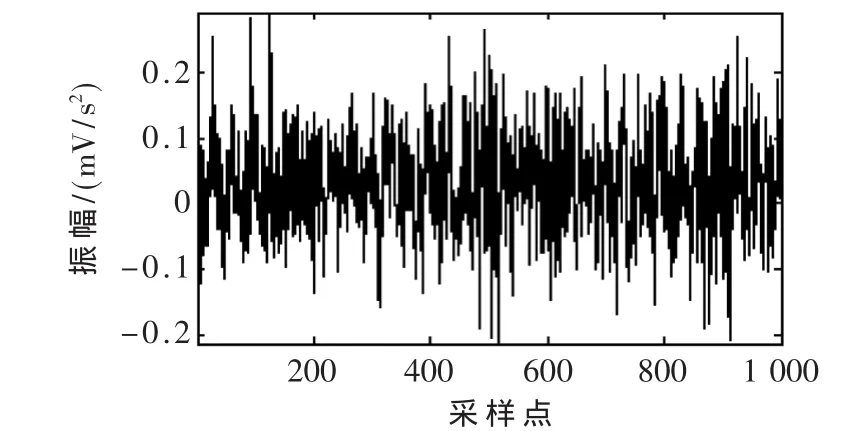
圖3 滾動體點蝕振動信號

圖4 內圈單點故障振動信號

圖5 外圈點蝕故障振動信號

由于每段數據提取的特征個數為20個，因此將分類器的輸入層神經元個數設置為了20個。通過實驗得到了最佳的隱含層神經元數量。輸出層神經元個數對應于4種故障，最終的神經網絡架構和參數設置如表1所示。

表1 測試的神經網絡架構及其參數設置

其中S-MPL代表了S型函數作為隱含層激勵函數的神經網絡系統。F1-MPL代表以式（4）中的函數作為激勵函數的神經網絡系統。對F1-MPL的訓練過程如圖6和圖7所示。圖6顯示的是利用本文算法的訓練過程，其中σ=0.5，初始值在 0～1之間隨機生成。圖 7展示了利用共軛梯度法作為訓練算法的收斂過程。共軛梯度法是介于最速下降法與牛頓法之間的一個方法，它僅需利用一階導數信息，但克服了最速下降法收斂慢的缺點，又避免了牛頓法需要存儲和計算Hesse矩陣并求逆的缺點，學習率選為1.2。

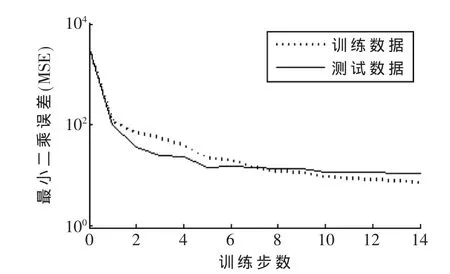
圖6 本文算法訓練過程

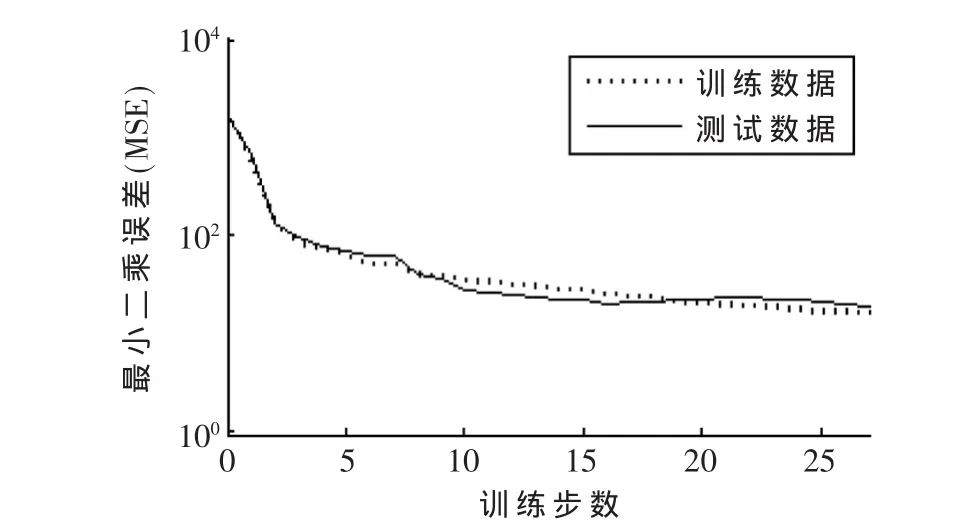
圖7 共軛梯度算法訓練過程

從圖6和圖7中的對比可以看出，利用本文提出的算法在第5次更新時就基本可以達到穩定，具有穩定性高、收斂速度快的特點。

3.3 分類結果

通過訓練后兩種神經網絡對4類信號最終的分類結果如表2所示。

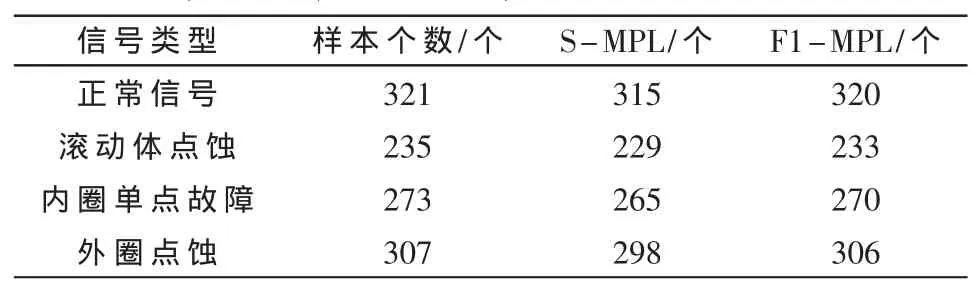
表2 神經網絡算法的比較結果

其中樣本個數一欄分別表示了4種類型的信號的樣本個數，S-MPL、F1-MPL分別指的是通過 S-MPL網絡和F1-MPL網絡分類正確的4種信號的數目。因此可以計算出兩種神經網絡算法的分類精度如表3所示。

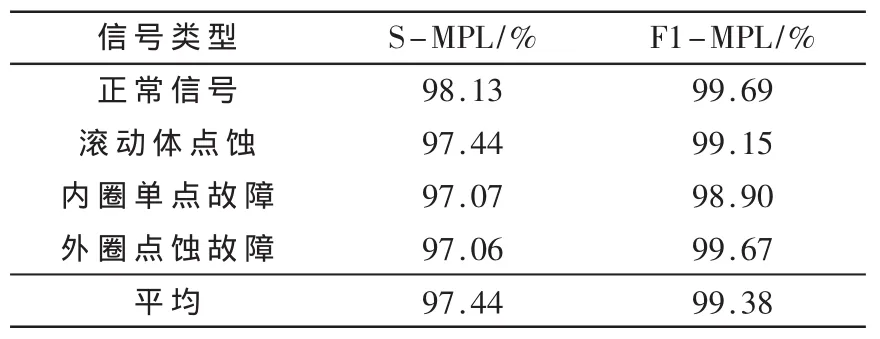
表3 分類器的分類精度比較結果

從表1中看出，本文的訓練算法比傳統固定型的S型函數更加耗時，這是由于將可變參數引入到激勵函數中后，系統在訓練時往往需要更多的運算。然而訓練樣本的收斂精度也有所提高，這表明了本文算法訓練精度也更高，因此可以推測，自適應性的神經網絡應用到其他問題當中時，比傳統的神經網絡更加容易搜索到全局最優值。

表2和表3證明了將本文的訓練算法應用在解決滾動軸承故障診斷問題方面的優越性，取得了更高的分類精度。對于正常信號、滾動體點蝕振動信號、內圈單點故障信號、外圈點蝕故障信號的分類精度分別可以達到99.69%、99.15%、98.90%、99.67%，平均分類精度可以達到99.38%。

4 結論

本文對傳統的S型激勵函數進行了改進，提出一種自適應性的神經網絡分類器；基于馬爾可夫鏈對神經網絡進行訓練，提高了網絡訓練速度；最后，將該分類器應用到滾動軸承故障診斷問題中。結果證明，使用該分類器可以比傳統的S型神經網絡分類器獲得更高的分類精度。

[1]唐貴基，范德功，胡愛軍，等.基于小波包能量特征向量神經網絡的旋轉機械故障診斷[J].汽輪機技術，2006(3)：215-217.

[2]張來斌，崔厚璽，王朝暉，等.基于信息熵神經網絡的風力發電機故障診斷方法研究[J].機械強度，2009(1)：132-135.

[3]BURSE K，YADAV R N，SHRIVASTAVA S C.Channel equalization using neural networks：a review[J].IEEE Transactions on Systems，Man，and Cybernetics Part C-Applications and Reviews，2010，40(3)：352-357.

[4]BILDIRICI M，ALP E A，ERSIN O O.TAR-cointegration neural network model：An empirical analysis of exchange rates and stock returns[J].Expert Systems with Applications，2010，37(1)：2-11.

[5]KANG M，PALMER-BROWN D.A modal learning adaptive function neural network applied to handwritten digit recognition[J].Information Sciences，2008，178(20)：3802-3812.

[6]滕輝.一種改進的神經網絡學習算法研究[J].科技通報，2012(4)：97-98.

[7]鄭緒枝，夏薇，雷靖.一種改進的Jacobi正交多項式的BP神經網絡算法[J].云南大學學報(自然科學版)，2011(S2)：188-191.