高空作業平臺剪叉機構的受力計算
趙學龍,劉巧珍,馬志剛,杜 丹(江蘇柳工機械有限公司,江蘇 鎮江 2 1 2 0 0 5)
剪叉機構在國內應用已比較廣泛,如物流升降平臺、舞臺升降機械、高空作業機械等。剪叉式高空作業平臺一般用于需要垂直升降的各類場所,與其它結構形式的高空平臺相比,剪叉式平臺的穩定性較好、安全性高。因工作需要,筆者對用于高空作業平臺的剪叉機構的受力計算進行了研究。
1 剪叉機構形式
根據剪叉臂的層數不同,剪叉機構分為單層、雙層、三層、四層、五層等。根據剪叉臂的組數不同,剪叉機構分為單剪叉式臂、雙剪叉式臂、多剪叉式臂等。組數指的是剪叉在同一層中數量的重復,而層數指的是剪叉在上下方向的疊加。
出于穩定性的考慮,剪叉機構一般是雙剪式。在物流升降平臺和舞臺升降機械中,一般是單層和雙層剪叉機構。在高空作業平臺中,三層、四層、五層的剪叉機構都有應用。三層和四層剪叉式高空平臺用一個舉升油缸驅動,五層剪叉式高空平臺用兩個舉升油缸驅動。
2 虛功原理
與裝載機、挖掘機等其它工程機械相比,剪叉平臺工作機構的運動比較簡單,只有作業平臺的上下運動。工作時,液壓泵向舉升油缸泵入油液使舉升油缸向上舉升;下降時,在自重作用下舉升油缸中的油液被壓回油箱,作業平臺下落。由于是載人作業,其上下運動速度都比較慢,在機構受力計算時一般不考慮慣性力影響。
剪叉機構計算的核心是舉升油缸力的計算。知道了任意位置的舉升油缸力,就可指導液壓系統的設計;可以進一步計算出桿件中的鉸點力,進行桿件的強度校核。剪叉機構是由多個桿件組成的桁架系統,對油缸力的計算一般是采用虛功原理。虛功原理使得計算過程簡單化,解題思路清晰易懂。
虛功原理的定義為:作用于質點系的所有主動力在任何虛位移中所作虛功的和等于零。對于剪叉機構,令工作載荷外力為W,其虛位移為δW。舉升油缸在剪叉機構中本來是被約束住的,將該約束解開用油缸力代替,用F表示,其虛位移為δF。于是根據虛功原理,可列出平衡方程

在式(1)中,工作載荷W已知,工作載荷的虛位移和油缸力的虛位移可以表示成位置的函數,當剪叉機構位置確定時,這兩個虛位移可認為是已知的,于是可解出油缸力F。
3 油缸力計算
下面用單油缸四叉機構來論述油缸力的計算過程。
四叉機構簡圖如圖1所示。機構中兩邊鉸點分別用A~N命名,中間鉸點用O1~O4命名,外載荷作用點W點在MN的中點處。舉升油缸下鉸點為K點,K點在桿AD上的投影點為J點。舉升油缸上鉸點為Q點,Q點在桿EH上的投影點為P點。令單根叉臂長為L,PO3長度為b,JO1長度為a,單根叉臂與水平面的夾角為α,油缸長度方向與水平面的夾角為β。JK長度為L1,PQ長度為 L2。

圖1 四叉機構簡圖
以剪叉臂上與車架的固定鉸接點A點為坐標原點,以AB連線為X軸,以AM連線為Y軸建立直角坐標系。
列出K點和Q點的X坐標和Y坐標
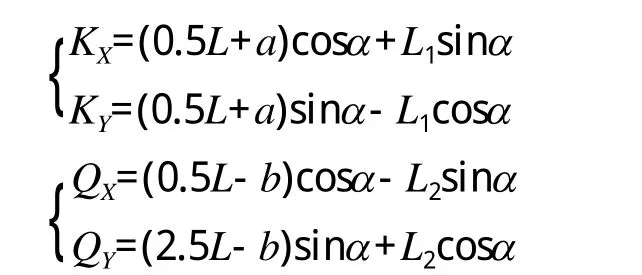
則有
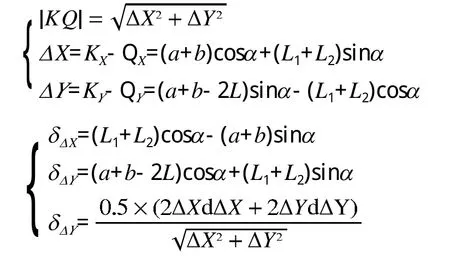
外力載荷W的Y坐標為WY=4L sinα,
則δWY= 4L cosα
令油缸力為FKQ,工作平臺載荷為W,
則

變換得

按式(3)的算法,假定載荷都作用在工作平臺上,而忽略了叉臂組件的重量。實際上由于工作載荷的重量和叉臂的重量在數值上為一個量級,忽略叉臂組件重量后所得到的油缸力結果與真實結果有很大誤差,需要對公式(3)進行完善。
為使計算簡單,將每層叉臂的重量集中到相應中點O 處,每一層的重量為W,則

變換得

式(5)就是考慮了叉臂組件重量的油缸力計算公式。注意,式(5)中的載荷重量W包含工作載荷重量和作業平臺自重。
令L=2 000mm,a=700mm,b=670mm,L1=170mm,L2=160mm,各層叉臂重量Wi=150kg,平臺重量WT=250kg,載荷重量WW=300kg,將各值代入公式,可算得油缸力。油缸力隨叉臂桿件傾角α的曲線圖見圖2。

圖2 油缸力曲線圖
4 鉸點力計算
對液壓系統,知道剪叉機構在任意位置的油缸力大小就足夠了。而對結構件系統而言,這是不夠的,還需要計算叉臂組件的各個桿件鉸點的受力,從而校核桿件的強度。
繪制最下層叉臂的受力簡圖,見圖3和圖4。對最下層叉臂進行整體分析得

圖3 AD桿受力簡圖

圖4 BC桿受力簡圖

對BC桿,由X、Y向受力平衡和對C點取矩列平衡方程,得

對AD桿,由X、Y向受力平衡和對O1點取矩列平衡方程,得

將已知數據代入,逐個算出有關未知數。
根據上面的過程,鉸點C和D的鉸點力已解出,可重復上面的步驟算出第二層各鉸點的力。重復這樣的步驟可算出所有層各鉸點的力。
類似于建筑結構中的多層樓房,上層叉臂的重量逐層疊加到下層叉臂上,因而剪叉機構中最下層的叉臂桿件受力最危險。通過前面的油缸力計算,剪叉機構在初始位置處受力一般最大。這樣只需校核最下層剪叉機構在初始位置的受力即可。
5 結 論
本文對用于高空作業平臺的剪叉機構的受力計算進行了研究,并成功應用于生產實踐。按照真實數據代入的舉升油缸力結果與實測結果的誤差在10%以內,即本文所述方法在工程應用上是可行的。 O
[1] 于永江,郭云緋,高 暢.虛功原理法進行多層剪叉機構的受力分析[J].機械設計與制造,2008,(3):84-86.
[2] 曾午平.剪叉式液壓升降臺參數化設計及結構分析[D].太原:太原科技大學碩士論文,2009.
[3] 哈爾濱工業大學理論力學教研室.理論力學(第6版)[M].北京:高等教育出版社,2002.

