攪拌摩擦焊接全過程熱力耦合有限元模型

崔俊華，柯黎明，劉文龍，郭正華，趙剛要，方 平

（1西北工業大學 材料學院 摩擦焊接陜西省重點實驗室，西安710072；2南昌航空大學輕合金加工科學與技術國防重點學科實驗室，南昌330063）

攪拌摩擦焊接（Friction Stir Welding，FSW）是由英國焊接研究所THOMAS等［1］于1991年發明的一種新型固相連接技術。FSW克服了熔焊時產生的諸如氣孔、裂紋、大變形等缺陷，以優質、高效、節能和無污染的特點廣泛應用于航空、航天以及汽車等領域。由于FSW過程是一個溫度變化、組織結構轉變、應力應變和金屬流動等方面相互耦合、共同作用的復雜過程，單純采用理論解析和實驗方法難以準確、有效地解決FSW的實際問題，特別是FSW過程溫度場和焊縫金屬塑性流動行為的研究。有限元模擬技術以良好的可視化和過程再現性優點，已成為國內外FSW研究的趨勢。Schmidt等［2］基于ABAQUS／Explicit建立了完全熱力耦合動態分析模型，該模型能夠模擬熱力條件下的穩定焊接階段。Xu等［3］將FSW看成穩態過程，采用ALE技術與預設溫度場方式建立了FSW穩定焊接階段熱力耦合模型。張昭等［4］基于ALE技術建立了6061－T6鋁合金焊接構件FSW穩定焊接階段完全熱力耦合模型。鄢東洋等［5］采用引入熱源模型的解析方法，建立了FSW穩定焊接階段分析模型。Guo等［6］基于ALE技術建立了FSW過程的穩定焊接階段熱力耦合模型。由于無法克服網格高度畸變問題，而采用預先在焊件上設置通孔的處理方式，僅能實現穩定焊接階段的仿真分析。上述處理方式導致穩定焊接階段初始時刻的溫度場和塑性變形場與實際情況不符，且因攪拌頭端部熱力條件發生了改變，使得模擬結果無法真實反映攪拌頭端部周圍的溫度場、塑性變形場和材料的流動行為。FSW初始階段產熱是FSW過程進入穩定焊接的基礎和關鍵，在建立攪拌摩擦焊接過程模型中不應被忽略。Mandal等［7］基于ABAQUS／Explicit建立了FSW 下壓階段的熱力耦合有限元模型。Hamilton等［8］和Yu等［9］基于ABAQUS／Explicit嘗試建立FSW 全過程的熱力耦合模型，但兩者模型獲得的溫度場和塑性變形場與實驗研究的結果出入較大，其中后者所建模型無法預測應力場和塑性變形場。

基于FSW過程有限元模型對焊接過程研究的重要性，以及現有有限元模型的缺陷，為更準確地反映FSW過程的溫度場和塑性變形情況，本工作在ABAQUS軟件平臺上建立攪拌摩擦焊接全過程（下壓階段和穩定焊接階段）熱力耦合有限元模型，基于ALE網格自適應技術對網格及邊界條件進行合適處理，解決了焊接過程中網格高度畸變問題。模擬分析了6061鋁合金焊件焊接過程溫度場和材料塑性變形場，并與實驗進行對比。

1 有限元模型

1.1 幾何模型

焊接構件為40mm×40mm×3mm的完整板材，攪拌針端部直徑6mm，錐角20°，軸肩直徑18mm，軸肩表面帶有1.5°的凹角，邊緣處有半徑為0.5mm的倒圓角。在有限元模型中攪拌頭設定為解析剛體，如圖1所示。

1.2 材料定義

采用Johnson－Cook本構模型［10］描述FSW 過程中局部高溫、高速、高壓的大變形和高應變速率下材料的熱力學行為（式（1））。采用6061鋁合金［4，11］材料焊接構件驗證模型，其相關參數如表1所示。

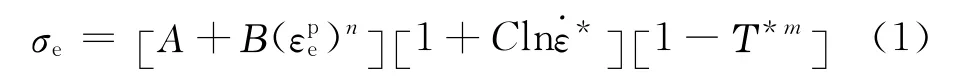
式中：σe為Von Mises流動應力；A為材料屈服強度；B為冪指前系數；C為應變率敏感指數；m為溫度軟化指數；n為加工硬化指數；εpe為等效塑性應變；＊＝pe／0，為相對等效塑性應變率，其中pe為等效塑性應變率，0為等效應變率，取0＝1.0s－1；T＊＝為無量綱溫度，其中Tm，Tr分別為材料的熔點和室溫溫度。

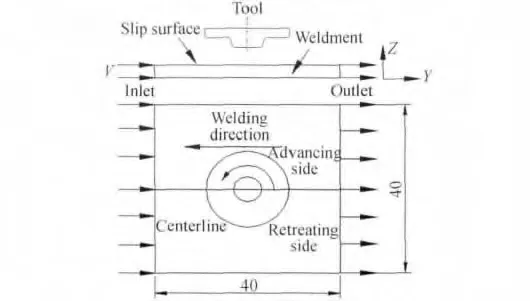
圖1 6061鋁合金焊件幾何尺寸和邊界條件Fig.1 Geometry and boundary conditions of 6061 aluminum alloy weldment

表1 6061鋁合金材料參數Table1 Material parameters of 6061aluminum alloy

1.3 網格劃分

采用八節點六面體線性實體減縮積分單元C3D8RT作為網格單元。該單元可以高效進行FSW過程中復雜的熱力耦合問題的求解計算，并且對網格扭曲敏感性低，具有沙漏效應，抗畸變能力強。在進行網格劃分時，考慮到下壓過程的大變形情況和穩定焊接階段攪拌頭與焊件穩定接觸的需要，將焊件劃分為均勻網格。驗證模型采用的6061鋁合金焊接構件有限元模型如圖2所示。RP為攪拌頭參考點。

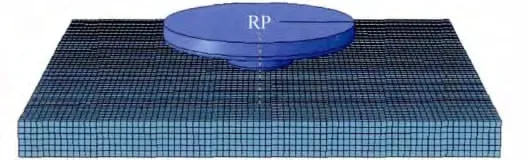
圖2 6061鋁合金焊件有限元模型Fig.2 Finite element model of 6061aluminum alloy weldment

1.4 ALE自適應網格處理

ALE自適應網格技術全稱為“任意的拉格朗日－歐拉自適應網格”，集合了Lagrangian和Eulerian方法的優越性［3］，允許材料獨立于網格運動。為解決初始焊接階段和穩定焊接階段由材料流動導致的網格畸變問題，應用ALE技術將這兩階段作為Lagrangian與Eulerian問題來處理。

在ABAQUS中，ALE技術的實現包含三種邊界設定：Lagrangian邊界、Slip邊界和Eulerian邊界。本工作采用Slip邊界模擬攪拌頭和工件表面的接觸，該邊界網格被強制約束與物質點同時朝表面的法線方向運動，而在切線方向可以同物質點分開，如此能夠避免由攪拌頭高速旋轉導致的網格畸變問題，實現下壓階段攪拌頭插入焊件的過程。而Eulerian邊界上物質和網格可以單獨運動，可以保證在下壓階段結束后順利過渡到穩定焊接階段。

1.5 熱邊界條件處理

將FSW熱傳導過程簡化為單一熱傳導，即直接給焊件相應表面設置一定間隙熱傳系數，其中室溫（20℃）下工件底面、工件表面和側面的間隙熱傳系數分別為1000，100，100W／（m2·K）。

經散熱后，焊件中的溫度分布可通過公式（2）計算得出

式中：q為單位時間內通過間隙的熱流量；θA與θB分別為間隙兩面的溫度值；h為間隙熱傳系數。

“用善騎射，殺首虜多，為漢中郎”，“用善騎射”譯為“He proved himself a skillful horseman and archer”。“用”在這里是介詞，表示原因，譯為“因為”。英譯中用“prove”這個動詞來翻譯，沒有凸顯出原文中的因果關系，只是說明李廣有善騎射的才能。

另外，攪拌頭與工件材料之間也發生熱交換作用，且兩者之間接觸與間隙同時存在換熱情況，在模型接觸設置的熱傳導屬性定義中，通過采用攪拌頭與工件之間的接觸應力來確定兩者之間接觸與間隙情況下的熱傳導系數，進而確定攪拌頭與焊件之間的熱交換。

由于焊接過程中存在焊縫金屬的高度塑性變形，本模型考慮了金屬材料的塑性變形能對溫度的影響，在材料模型的熱屬性中通過定義塑性變形功轉換為熱量的系數來定義塑性變形能對溫度的影響。

1.6 接觸條件處理

本模型將FSW過程中攪拌針與焊件之間的接觸假定為滑移摩擦類型，且由于接觸面之間的相對滑動或轉動量很大，往往大于接觸面上的單元尺寸，將攪拌頭與工件的接觸關系假設為有限滑移模式。考慮到FSW過程中摩擦行為極為復雜，難以達到理想摩擦狀況，本工作采用的摩擦模型為罰摩擦模型。罰摩擦允許滑移過程中發生單元特征長度很小部分的“彈性滑移”，即在黏結的接觸表面間發生一個很小相對運動。在ABAQUS中設定FSW過程中罰摩擦模型的摩擦因數為0.3［2］。

1.7 模型穩定性驗證

采用建立的模型模擬攪拌針轉速為40rad／s、焊速為2mm／s工藝條件下，6061鋁合金構件的攪拌摩擦焊接過程。設定質量放大因子200000，采用ABAQUS／Explicit模塊中求解獲得的動能與內能之比曲線和變形材料動能曲線來說明本模型計算結果的可靠性和穩定性［12］。當變形材料的動能與內能比值在大部分模擬時間內低于0.05時，表明所采用的質量放大因子是可以接受的。圖3為數值模擬過程動能與內能之比曲線，焊接開始約0.2s后動能與內能的比值處于0.01以下，小于0.05，且保持較小值不變，模擬所取質量放大因子是可以接受的。當變形材料的動能本身或者一些代表性節點的速度變化足夠平滑時，表明計算過程和計算結果是穩定的。圖4為數值模擬過程焊接件的動能變化曲線。在進入穩定焊接階段后動能曲線基本保持穩定，計算過程和計算結果是穩定的。說明本模型的計算結果在理論上是可靠、穩定的。

圖3 6061鋁合金焊件有限元模擬動能與內能之比Fig.3 The ratio of kinetic energy and internal energy of 6061aluminum alloy weldment finite element simulation

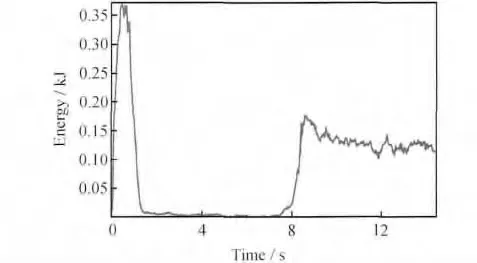
圖4 6061鋁合金焊件有限元模擬動能變化曲線Fig.4 The kinetic curves of 6061aluminum alloy weldment finite element simulation

2 模型分析

2.1 焊接工藝參數

攪拌針轉速為40rad／s，焊速為2mm／s。整個焊接過程包括8.4s下壓階段和6s穩定焊接階段。

2.2 溫度場

圖5為FSW全過程焊件縱截面溫度場隨時間變化圖。當攪拌頭剛開始插入工件時，工件的高溫區主要位于攪拌頭端部下方且成“V”形，攪拌頭前后方的溫度場成對稱分布。隨著攪拌頭的不斷插入，工件材料向外擠出，溫度不斷上升，并向周圍擴散。當攪拌頭軸肩端面與工件上表面接觸后，高溫區逐漸向攪拌針根部轉移，直到兩者完全接觸。

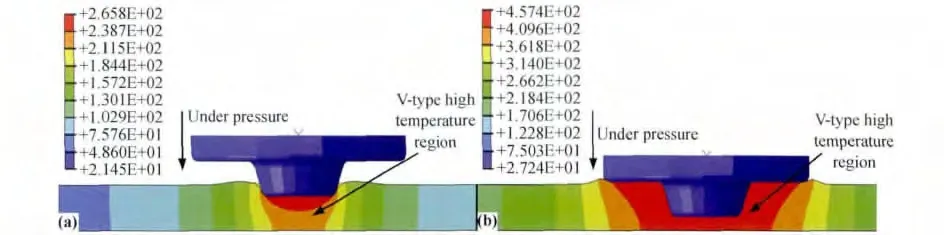
圖5 6061鋁合金焊件縱截面上溫度場變化（a）下壓3s；（b）下壓8.4sFig.5 The temperature field changes of 6061aluminum alloy weldment at the longitudinal section（a）under pressure 3s；（b）under pressure 8.4s

圖6為FSW過程焊件水平方向上溫度場隨時間變化圖。整個焊接過程最高溫度在463℃左右，低于材料熔點值，未出現材料熔化的現象，符合固相連接特性。國內外研究學者一致認為在穩定焊接階段焊縫處的最高溫度基本保持不變，其數值大小主要由攪拌頭的旋轉速率和焊接速率所決定。而本模型所得最高溫度與McClure等［13］在相同焊接工藝參數下得到的FSW過程最高溫度值450℃吻合。

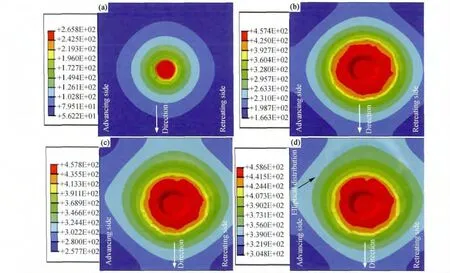
圖6 6061鋁合金焊件水平方向溫度場變化（a）下壓3s；（b）下壓8.4s；（c）穩定焊接2s；（d）穩定焊接6sFig.6 The temperature field changes of 6061aluminum alloy weldment at the horizontal（a）under pressure 3s；（b）under pressure 8.4s；（c）stable welding 2s；（d）stable welding 6s

由圖6（a），（b）可知，攪拌頭軸肩與焊件上表面完全接觸前，溫度場攪拌頭前后對稱分布，直到進入穩定焊接階段。軸肩與焊件上表面接觸后，焊件從上到下溫度場呈現高的溫度梯度（圖5（b），6（b））。進入穩定焊接階段后，隨著攪拌頭不斷遷移，溫度場近似地呈橢圓形，其前方的溫度梯度逐漸大于其后方的溫度梯度，且最高溫度值只有微小的變化，如圖6（c），（d）所示。

由于在穩定焊接階段，焊件上表面溫度值主要受攪拌頭旋轉速率和焊接速率影響，焊件板厚與焊件下表面墊板之間的熱交換對上表面影響較小。為進一步驗證本模型在模擬6061鋁合金FSW過程中溫度場的準確性，在相同旋轉速率（390r／min）和焊接速率（2.36mm／s）下，焊接穩定狀態下焊件上表面橫向溫度分布值與Reynolds等［14］所得到的焊件上表面橫向溫度分布值進行比較（圖7），發現模擬所得溫度值與實驗值吻合較好，說明建立的模型是準確有效的。

建立的模型與Hamilton等［8］建立的模型所得結果有明顯不同，后者模型所得溫度場的溫度過高，且等效塑性應變場與實際存在較大出入，而本文所得焊接階段的最高溫度值低于材料熔點，符合FSW固相連接特性，模型真實、可靠地反映FSW全過程。

2.3 塑性變形場

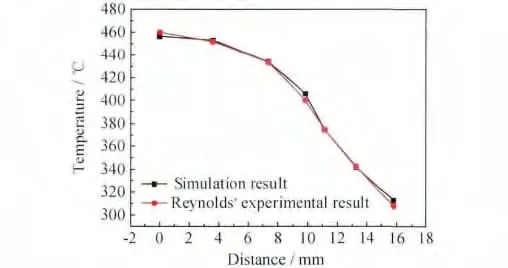
圖7 6061鋁合金焊件上表面溫度分布值模擬結果與Reynolds實驗結果對比Fig.7 Comparison of simulation and Reynolds’experimental results of temperature distribution on the upper surface of 6061aluminum alloy weldment

圖8為攪拌頭下壓階段不同時刻的等效塑性應變場。圖8（a）為攪拌頭下壓5s時等效塑性應變場，此時只有攪拌針端部區域與焊件材料之間產生旋轉摩擦作用，故等效塑性應變場主要位于攪拌針端部附近，且攪拌針邊緣離中心最遠，線速率最大，從而導致高應變區位于攪拌針邊緣處。當攪拌頭軸肩與焊件上表面材料接觸后，焊縫區上部金屬材料塑性變形場迅速增大，但限制在軸肩范圍內，如圖8（b）所示。

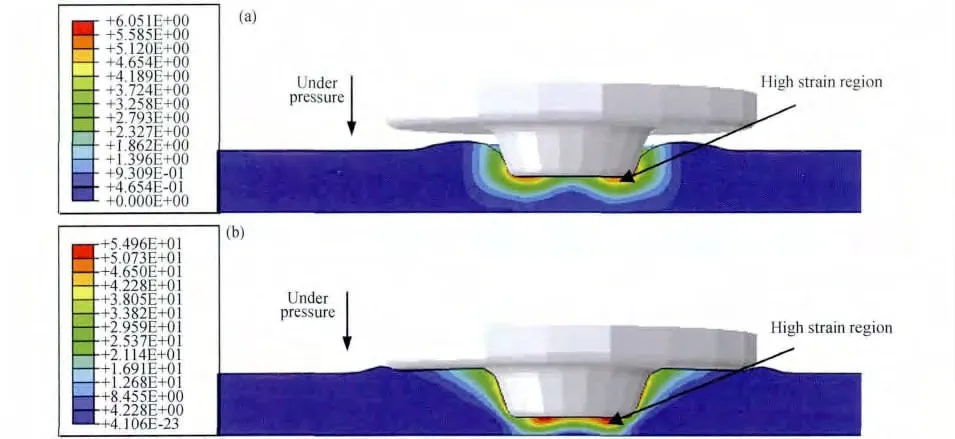
圖8 6061鋁合金焊件的等效塑性應變場（a）下壓5s；（b）下壓8.4sFig.8 The equivalent plastic strain fields of 6061aluminum alloy weldment（a）under pressure 5s；（b）under pressure 8.4s

圖9為穩定焊接6s后焊件縱截面等效塑性應變場分布圖。攪拌頭前方等效塑性應變梯度高于攪拌頭后方，且局限在一個很小范圍內；攪拌頭前方等效塑性應變梯度最大，遠大于其后方，且等效塑性應變場主要分布于攪拌頭后方。等效塑性應變值的大小直接反映了該區域材料變形的劇烈程度，在穩定焊接階段，焊縫處的材料主要是受攪拌頭的旋轉和擠壓作用而產生繞攪拌頭旋轉運動和向后方端部沉積，這必然導致在攪拌頭后方端部產生較大的等效塑性應變值，與實驗研究結果吻合［15］。

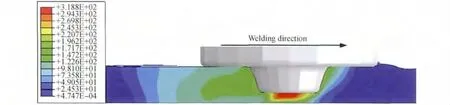
圖9 6061鋁合金焊件縱截面上穩定焊接6s時等效塑性應變場Fig.9 The equivalent plastic strain fields of 6061aluminum alloy weldment at the longitudinal section during stable welding 6s

圖10為穩定焊接6s后焊件后方橫截面處等效塑性應變場。等效塑性應變區近似成“V”形分布，高等效塑性應變區以不規則環狀分布于焊縫中下部，且其中心偏向前進邊側，與XU等［16］實驗所得焊核分布形態相同，前進邊側變形程度較返回邊側更劇烈，且變形范圍更大，尤其是焊件上半部分。

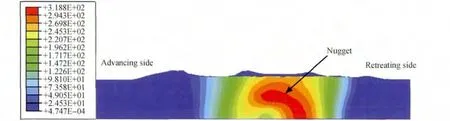
圖10 6061鋁合金焊件橫截面上穩定焊接6s時等效塑性應變場Fig.10 The equivalent plastic strain fields of 6061aluminum alloy weldment at the cross section during stable welding 6s

圖11為穩定焊接6s后焊件水平方向靠近上表面等效塑性應變場分布。可以看出，在FSW過程中，材料的等效塑性應變場在攪拌頭后方呈弧形環狀結構分布，等效塑性應變區偏向前進邊側。模擬所得水平方向等效塑性應變場前進邊側等效塑性應變值明顯大于返回邊側，與實驗結果“前進邊的標示材料層破壞的程度明顯大于返回邊的現象說明，在前進邊所發生的材料變形劇烈程度更大”［15］相吻合。

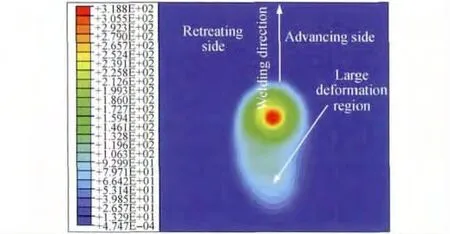
圖11 6061鋁合金焊件靠近上表面穩定焊接6s時水平方向等效塑性應變場Fig.11 Equivalent plastic strain fields of 6061aluminum alloy weldment at the horizontal near upper surface during stable welding 6s

3 結論

（1）基于ALE網格自適應技術解決了攪拌摩擦焊接過程中出現的網格高度畸變問題。

（2）實現了攪拌摩擦焊接全過程的溫度場和塑性變形場的仿真分析，且所得焊縫處等效塑形應變場分布與實驗所得焊縫處組織結構具有良好對應性。

（3）模擬所得6061鋁合金FSW過程最高溫度值與實驗最高溫度值之間的誤差為2.89%，且焊件上表面在橫向溫度的分布與實驗數值有良好的吻合。

［1］THOMAS W M，NICHOLAS E D，NEEDHAM J C，et al.Friction Stir Welding［P］.UK Patent：9125978.8，1991－12－06.

［2］SCHMIDT H，HATTEL J.A local model for the thermo mechanical conditions in friction stir welding［J］.Modelling and Sim－ulation in Materials Science and Engineering，2005，13（1）：77－93.

［3］XU S，DENG X.A three dimensional model for the friction stir welding process［A］.CD－ROM Proceedings of the 21st Southeastern Conference on Theoretical and Applied Mechanics（SECTAM XXI）［C］.Orlando，Florida：University of Central Florida，2002.699－704.

［4］張昭，別俊.攪拌摩擦焊接過程數值仿真的完全熱力耦合模型［J］.中國機械工程，2008，19（10）：1240－1245.ZHANG Z，BIE J.Fully coupled thermo－mechanical model for numerical simulation of friction stir welding process［J］.Chinese Journal of Mechanical Engineering，2008，19（10）：1240－1245.

［5］鄢東洋，史清宇，吳愛萍，等.攪拌摩擦焊接的熱力耦合分析模型［J］.機械工程學報，2010，46（16）：106－112.YAN D Y，SHI Q Y，WU A P，et al.Developmental thermalmechanical coupled analysis model for friction stir welding［J］.Journal of Mechanical Engineering，2010，46（16）：106－112.

［6］GUO Z H，ZHAO G Y，KE L M，et al.Thermo－mechanical coupled analysis of deformation behavior in friction stir welding process of aluminum 7075plate with conical pin［J］.Advanced Materials Research，2011，338：618－621.

［7］MANDAL S，RICE J，ELMUSTAFA A A.Experimental and numerical investigation of the plunge stage in friction stir welding［J］.Journal of Materials Processing Technology，2008，203（1－3）：411－419.

［8］HAMILTON R，MACKENZIE D，LI H J.Multi－physics simulation of friction stir welding process［J］.Engineering Computations，2010，27（8）：967－985.

［9］YU M，LI W Y，LI J L，et al.Modeling of entire friction stir welding process by explicit finite element method［J］.Materials Science and Technology，2012，28（7）：812－817.

［10］JOHNSON G R，COOK W H.Fracture characteristics of three metals subjected to various strains，strains rates，temperatures and pressures［J］.Engineering Fracture Mechanics，1985，21（1）：31－48.

［11］ZHANG Z，CHEN J T.Computational investigations on reliable finite element－based thermo－mechanical coupled simulations of friction stir welding［J］.Adv Manuf Technol，2011，60（9－12）：959－975.

［12］張昭，張洪武.接觸模型對攪拌摩擦焊接數值模擬的影響［J］.金屬學報，2008，44（1）：85－90.ZHANG Z，ZHANG H W.Effect of contact model on numerical simulation of friction stir welding［J］.Acta Metallurgica Sinica，2008，44（1）：85－90.

［13］McCLURE J C，FENG Z，TANG W，et al.A thermal model of friction stir welding［A］.Proc 5th Int Conf on Trends in Welding Research［C］.Pine Mountain：ASM International，1998.590－595.

［14］KHANDKAR M Z H，KHAN J A，REYNOLDS A P.A thermal model of the friction stir welding process［A］.ASME International Mechanical Engineering Congress ＆ Exposition［C］.New Orleans，Louisiana：ASME，2002.115－124.

［15］柯黎明.攪拌摩擦焊接頭成形規律研究［D］.北京：清華大學，2007.KE L M.An investigation on the formation mechanism of the friction stir welds［D］.Beijing：Tsinghua University，2007.

［16］XU S，DENG X.A study of texture patterns in friction stir welds［J］.Acta Materialia，2008，56（6）：1326－1341.