空間機械臂視覺測量技術研究

劉 玉，陳 鳳，黃建明，魏祥泉

(上海宇航系統工程研究所，上海201108)

1 引言

空間站的組裝建造、在軌檢測、維護維修、輔助航天員出艙活動、支持空間應用［1］等都需要借助空間機械臂，完成多種復雜的艙外操作。機械臂視覺系統作為空間機械臂遙操作控制的伺服輸入，會直接影響空間機械臂的控制精度，進而進一步影響機械臂的空間操作能力。

空間機械臂視覺測量技術主要包括手眼關系標定、標志器識別、相對三維位姿測量等關鍵技術［2-6］。目前國外已經在空間站使用的標志器各有優缺點，結合我國空間站實際任務需求，選擇設計的標志器上應有容易識別的點、線以及圓等豐富的特征信息，以為后續機械臂視覺高精度測量奠定基礎。本文重點對標志器識別、相對三維位姿測量等關鍵技術進行深入研究，并以加拿大機械臂為例提出了一種基于邊緣特征的標志器識別方法和基于非迭代的位姿測量算法，并給出了仿真實驗結果以及機械臂原理樣機的實驗結果。

2 空間機械臂視覺測量技術

2.1 空間機械臂視覺測量技術流程

空間機械臂視覺測量技術的主要工作流程如圖1所示。

圖1 空間機械臂視覺測量技術流程框圖Fig.1 The flow chart of the vision measurement technology of Space Robotic Arm

首先，通過手眼關系標定技術確定空間機械臂末端與攝像機之間的關系;其次，通過手眼相機采集標志器圖像，利用圖像處理與模式識別等技術完成標志器的識別，從中提取標志器特征信息;然后，利用相對三維位姿測量技術獲得目標標志器相對攝像機的位置與姿態，并通過手眼關系矩陣確定目標標志器相對機械臂末端的位置姿態;最后，將解算出的標志器相對機械臂末端的位置姿態信息作為空間機械臂視覺伺服控制的輸入，反饋給機械臂伺服控制器。伺服控制器則可根據實際需要發送控制指令給視覺測量系統執行相應的功能。

2.2 手眼關系標定技術

假定攝像機內/外部參數已標定，那么標定手眼關系則主要通過設計合理的機械臂運動，計算出手眼關系矩陣。如圖2所示，A為機械臂末端坐標系在這兩個相應位置間的相對變換矩陣，B則為攝像機坐標系在這兩個不同位置間的相對變換矩陣，則有:AX=XB。機械臂的手眼關系標定即轉換為求解上述方程［7］，具體求解方法可詳見文獻［8］。

圖2 手眼關系標定原理圖Fig.2 The principle of calibration of hand-eye relationship

2.3 標志器識別技術

2.3.1 標志器設計

為使空間機械臂接近抓捕目標并準確地對其進行定位，需要在抓捕目標上安裝標志器作為特征，并且標志器的設計應以與周圍物體顯著不同為原則。參考國外有關技術文獻，標志器設計一般有兩種:第一種是被動標志，第二種是主動標志。主動標志主動地輻射光能，被動標志包括特殊設計的觀測靶標和角反射器［2-6］。目前用于機械臂視覺測量的標志均采用被動標志，例如加拿大機械臂的十字靶標［2］(圖3)、日本實驗艙暴露平臺上的人工標志［4-5］等。由于被動標志中角反射器標志易受到雜光干擾，會增加目標識別算法的復雜性。因此，本文主要采用基于特殊設計的標志器，考慮到加拿大機械臂中設計的十字標志器上有容易識別的點、線以及圓等豐富的特征信息［2］，基本能夠滿足機械臂精細化操作要求，因此，本文主要參考該標志器進行設計。

圖4所示為本文設計的標志器，其上有14個有效特征點。攝像機坐標系定義和標志器坐標系定義一致。標志器坐標系的原點確定為白色圓環的圓心;x軸正方向為原點指向靶桿的負方向，y軸為較長白色線條之一的對稱線，z軸正方向為較短白色線條的對稱線的反方向，坐標系滿足右手法則。由于標志器上的直線特征比較明顯，根據較長白色線條和較短白色線條具體尺寸和位置關系，可以確定出標志器區域。

圖3 加拿大十字靶標Fig.3 The cross marker of the Canadian Robotic Arm

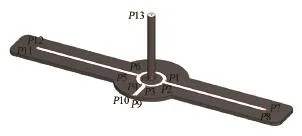
圖4 標志器上14個特征點Fig.4 The fourteen feature points in the maker

2.3.2 標志器識別

由于標志器上有明顯的邊緣特征，且存在互相平行的直線。因此，為充分識別標志器，關鍵是識別到正確的直線邊緣。圖5給出了本文的具體識別流程。其中，圖像預處理主要采用高斯濾波對圖像進行去噪處理，并采用自適應閾值法［9］對圖像進行二值化處理。下面重點對邊緣特征提取、邊緣特征匹配以及特征點提取作說明。

1)邊緣特征提取

在二值化圖像中，首先，采用Freeman鏈碼法［10］獲取以點序列形式表示的邊緣特征信息。然后，為避免程序處理過多的非標志物區域，對檢測到的區域進行篩選，提取每個區域的面積，凸凹性，最大包圍盒的長寬比信息并進行判斷，初步篩選出可能的標志器區域。最后，為進一步逼近邊緣信息，用更少的邊緣點信息表征邊緣信息，采用Douglas-Peucker算法［11］進行簡化處理，并以矢量化形式表征一個邊緣信息，矢量化信息主要包括邊緣線段的兩個端點，邊緣線段所在的輪廓等。

2)邊緣特征匹配

圖5 標志器識別流程Fig.5 The flowchart of maker identification

根據提取到的邊緣特征，需要依據標志器CAD模型提供的幾何形狀、尺寸信息以及直線段間的幾何位置關系對候選的邊緣特征進行匹配篩選，以得到標志器特征。首先，對邊緣特征中的直線段特征是否平行進行判斷，同時輔以直線段特征長度范圍、大致比例判斷等。這里采用方程xcosθ+ysinθ= ρ( ρ，θ為常數)來表達一根直線。兩直線平行，這意味著兩直線方程的θ參數差值小于指定閾值。通過該方法可得到平行線段組的集合。其次，在平行線段組合中，根據直線段特征是否共線、垂直，同時輔以直線段特征是否屬于同一個輪廓、長度范圍、大致比例等，尋找標志器中四條較長白色線條和兩條較短白色線條。若兩直線共線，則表明兩直線方程的ρ，θ參數的差分別小于相應的指定閾值;兩直線垂直，則表明兩直線方程的θ參數的差值的絕對值小于指定閾值。

3)特征點提取

根據識別出的標志器可進一步得到如圖4所示的P0到P13特征點。編號為P1～P12的特征點都是邊緣直線段間的交點，主要通過對邊緣直線分別進行擬合，然后計算兩條直線的交點精確定位。而特征點P0則直接根據提取到四條較長白色直線段間的中心線和兩條較短直線的中心線的交點得到。特征點P13則是標志器中間圓桿頂部圓的中心點，在圖像中則表現為橢圓中心點，一般通過在特定區域中采用最小二乘法擬合橢圓［12］得到。

2.4 相對三維位姿測量技術

根據標志器識別出的14個特征點信息，利用三維位姿解算方法可得到標志器相對攝像機的位姿。目前，基于單目視覺物體三維位姿求解算法有很多，大致可分為線性算法［13］和迭代算法［14］。線性算法可直接得到解析解，計算速度很快，但該算法對噪聲較為敏感。常用的迭代算法則精度較高，但需要提供較好的初始值，否則很難收斂到正確解。文獻［15］提出一種RPNP算法，該方法是一種非迭代算法，通過求解一元七次方程獲得最小平方誤差意義上的最優解。和傳統的非迭代法相比，該方法具有計算精度高，且能夠得到相對穩定的位姿解的優勢。因此，本文主要采用該方法實現相對三維位姿解算。RPNP算法的中心思想是將參考點劃分為3點子集而得到一個四次方程組，用該四次方程組的平方和構造代價函數，然后通過求解代價函數的導數確定最優解。該算法能夠穩定地處理平面情況、一般3D情況與準奇異情況，達到迭代算法精度水平，卻只占用很小的計算資源;能夠在較少冗余點(n≤5)的情況下得到比迭代算法更高精度的解;算法效率高，能夠高效處理大量參考點。RPNP算法的流程如圖6所示，總體可分解為以下四個步驟［15］:

圖6 RPNP算法的流程圖Fig.6 The flowchart of RPNP algorithm

1)選擇一個旋轉軸

假定，攝像機坐標系為OcXcYcZc，標志器坐標系為OoXoYoZo，如圖7所示。一般選擇邊集中投影長度最大邊‖PiPj‖對應的PiPj作為旋轉軸Za軸。為確定Za軸方向，端點Pi0和Pj0深度值必須知道。將n個參考點劃分為n-2個3點子集，即{Pi0Pj0Pk|k≠ i0，k≠ j0}。通過 P3P約束，每個子集可得到一個四次多項式，如式(1)所示所示。

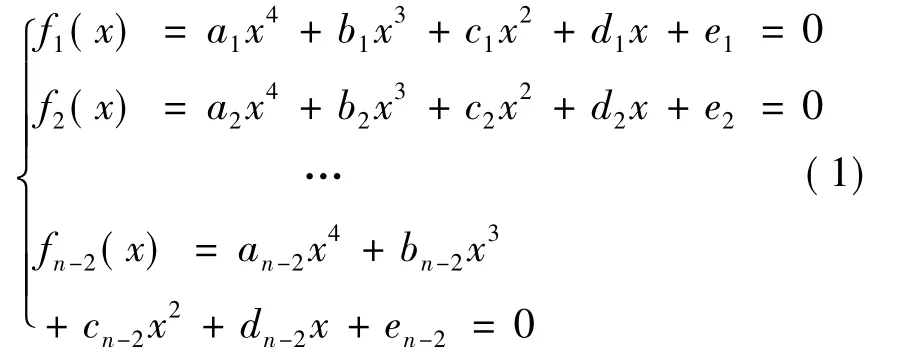
其中，未知參數x為Pi0的未知深度的平方。

圖7 三維參考點的二維投影Fig.7 The projection of the reference points

2)確定最小二乘誤差意義上的旋轉軸

通過最小二乘誤差方法［16］可解算上述方程組。首先，定義一個代價方程為其極小值可以通過求解它導數 F'=得到。F＇為一個一元七次方程，可通過特征值方法求解。當x與端點Pi0的深度被確定，另一個端點Pj0的深度可以通過P2P約束求得。最后可以得到坐標系OaXaYaZa的旋轉軸 Za=Pi0Pj0/‖Pi0Pj0‖ 。

3)求解旋轉角與平移向量

當OaXaYaZa的Za軸被確定，OaXaYaZa到攝像頭坐標系OcXcYcZc的旋轉矩陣可以表達如式(2)。

從三維參考點到二維歸一化圖像平面的投影可以表達為式(3)。

其中，(ui，vi)是圖像點 pi的歸一化坐標，t=是平移向量。

我們對上式各項組成2n×6齊次線性方程組即可解算出未知變量向量［c s txtytz1］T

4)計算標志器相對攝像機的位置姿態

在實際使用中，由于噪聲干擾，上述齊次線性方程組的解可能不滿足三角函數約束。因此，須對旋轉矩陣R施加正交約束。為對旋轉矩陣R進行歸一化處理［17］，首先使用未歸一化的R和t估計參考點在攝像機坐標系中的三維坐標，然后采用標準的三維對齊方法求解旋轉與平移矩陣。代價函數F為多項式的平方和，至多包含4個局部最小值。根據每個局部最小值估計標志器相對攝像機的位置，并選擇反向投影誤差最小的解作為算法輸出的最優解。

3 仿真與分析

本文算法結果均在CPU為Intel(R)Core(TM)2 Duo CPU，2.99 GHz，內存為 1.98 GB 的PC機上運行所得。操作系統為Windows XP，開發平臺為VS2008環境。

結合空間機械臂需要完成的空間操控任務，提出在0.5～1.5 m之間，視覺測量的位置精度≤0.005R(R表示機械臂末端與標志器之間距離)，姿態精度≤0.5°，算法處理周期≤250 ms。為充分驗證本文提出的空間機械臂視覺測量技術方法的可行性，本文分別對仿真圖像和機械臂原理樣機采集圖像進行驗證分析。

3.1 仿真圖像實驗結果與分析

圖像的數字仿真主要是建立包括攝像機模型、標志器模型在內的視覺成像仿真場景。這里主要采用Creator進行機械臂末端效應器與目標適配器即標志器的三維建模，并對模型表面材料屬性及紋理進行渲染;然后根據機械臂末端效應器與標志器之間相對運動關系，利用Vega視景仿真技術，結合相機參數，生成一組相對運動的圖像序列，其中圖像分辨率為1292*964。

圖8為標志器識別過程，其中(a)為原圖像，(b)為邊緣初步檢測結果，(c)為邊緣特征提取結果，(d)為根據標志器上邊緣直線之間平行關系得到的邊緣特征匹配結果，顯然還有許多干擾的平行直線對，(e)為根據標志器上直線對之間的關系進一步篩選得到的結果，(f)為標志器上特征點提取結果。通過這一組實驗可知，標志器識別算法能夠有效識別出標志器。

圖8 標志器識別過程Fig.8 The processof maker identification

圖9 給出了攝像機與標志器距離650.92 mm處的仿真圖像邊緣檢測及特征點提取結果，其中(b)中紅色加號表示提取出的特征點。圖10則給出了不同距離下根據特征點信息解算的位姿結果誤差曲線，由曲線可知，根據仿真圖像解算出的位姿測量結果誤差在技術指標要求的范圍內。由于本文主要采用基于非迭代思想的RPNP算法［15］實現位置姿態解算，因此，算法耗時量會明顯下降，通過實驗統計發現，本文算法對仿真圖像的處理速度能夠達到15 Fps，即算法處理周期在67 ms左右，顯然滿足預期速度指標要求。

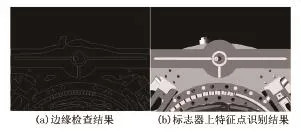
圖9 攝像機與標志器相距650.92 mm處檢測結果Fig.9 The result of maker identificationat the 650.92 mm distance

圖10 基于仿真圖像的相對位置姿態誤差曲線Fig.10 Theerror curve of the position and pose based on the simulated images

3.2 機械臂原理樣機實驗結果與分析

為進一步驗證提出的空間機械臂視覺測量技術有效性，又開展了其在機械臂原理樣機上的集成測試與驗證工作。測試過程中移動機械臂末端到不同位置，利用安裝于機械臂末端效應器的手眼相機進行實時圖像采集，實時識別標志器，并將相關特征點高亮動態顯示(圖11中紅色加號表示提取出的特征點)，以判斷標志器是否準確識別，識別之后進行三維位姿的實時測量和實時顯示。

圖11 攝像機相對標志器距離770.98 mm處檢測結果Fig.11 The result of maker identificationat the 770.98 mm distance

圖12 基于機械臂原理樣機的相對位置姿態測量誤差曲線Fig.12 Theerror curve of the position and pose based on the prototype of the robotic arm

為對測量精度進行驗證，在某一位置處利用激光跟蹤儀測量出機械臂末端與標志器之間的精確位姿，并與視覺測量結果進行比較，結果見圖12。其中，圖12(a)中的紅色‘-x-’線為位置理想誤差范圍，(b)中的紅色直線為姿態的理想誤差范圍。由圖12可以看出，隨著攝像機與標志器之間相對距離越來越小，測量誤差呈減小趨勢，并且位置測量誤差沒有超出理想誤差范圍，姿態測量誤差在相對距離1 m以內時也未超出理想誤差范圍，在相對距離1米以外，只有個別位置處姿態誤差較大。從總體趨勢來看，視覺測量算法精度基本滿足技術指標要求。圖13展示了攝像機在移動過程中識別的標志器效果。從中可看出，標志器識別相對準確，進一步說明本文提出算法的魯棒性。此外，實驗統計了針對實際圖像的算法耗時量，由于實際環境復雜，易受外界干擾影響，目前能達到平均每秒處理10幀圖像，即算法耗時量在100 ms左右，比仿真圖像的處理速度要慢些，但仍能滿足了預期速度指標要求。

圖13 攝像機與標志器在不同距離下識別結果Fig.13 The result of maker identification at the different distances

4 結論

本文主要對空間機械臂視覺測量技術進行了深入研究，梳理了空間機械臂視覺測量技術的技術流程，介紹了手眼關系標定技術、標志器識別技術以及相對三維位姿測量技術等關鍵技術，并以加拿大機械臂為標志器，提出了一種基于邊緣特征的標志器識別方法以及基于非迭代的三維位姿解算方法。最后，根據動力學仿真圖像以及機械臂原理樣機對本文提出的方法進行實驗驗證。實驗結果表明:本文提出的空間機械臂視覺測量方法合理可行，具有較強的工程應用價值。

［1］羅亞中，林鯤鵬，唐國金.空間站運營任務規劃技術評述［J］.載人航天，2012，18(2):7-13.

［2］Beland S，潘科炎.加拿大的空間機器人——從國際空間站的靈敏作業機器人到行星探測機器人［J］.控制工程(北京)，2001(2):22-29.

［3］Ravindran R，Doetsch K.Design aspect of the shuttle remote manipulator system［C］//Proc.of the AIAA Guidance and control conference，1982:456-465.

［4］Mack B.，McClure S.，Ravindran R.A ground testbed for evaluating concepts for the special purpose dexterous manipulator［C］//IEEE International Conference on Robotics and Automation，1991:884-889.

［5］Moe R.An Early In-Space Platform for Technology Development＆ Demonstration of Robotic Assembly ＆ Servicing［C］//AIAA 1st Space Exploration Conference:Continuing the Voyage of Discovery，2005.

［6］Inaba N，Oda M，Asano M.Rescuing a stranded satellite in space-Experimental robotic capture of non-cooperative satellites［J］.Transactions of the Japan Society for Aeronautical and Space Sciences.2006，48(162):213-220.

［7］張廣軍.視覺測量［M］.北京:科學出版社，2007:125-132.

［8］Shiu Y C，AhmadS.Calibration of wrist-mounted robotic sensors by solving homogenous transform equations of the form AX=XB［J］.IEEE Trans.Robotics and Automation，1989，5(1):16-29.

［9］Wu H M，Zheng X H.A New Thresholding Method Applied to Motion Detection［C］//Wuhan:Pacific-Asia Workshop.2008:119-122.

［10］裘鎮宇，危輝.基于Freeman鏈碼的邊緣跟蹤算法及直線段檢測［J］.微型電腦應用.2008，24(1):17-20.

［11］Douglas D H，Peucker T K.Algorithms for the reduction of the number of points required to represent a line or its caricature［J］.The Canadian Cartographer，1973，10(2):112-122.

［12］陳海峰，雷華，孔燕波，等.基于最小二乘法的改進的隨機橢圓檢測算法［J］.浙江大學學報(工學版):2008，42(8):1360-1364.

［13］張世杰，曹喜濱，李暉.交會對接航天器間相對位姿參數單目視覺測量的解析算法［J］.光學技術.2005，31(1):6-10.

［14］Fiore P D.Efficient Linear Solution of Exterior Orientation［J］.IEEE Trans Pattern Analysis and Machine Intelligence，2001，23(2):140-148.

［15］Li Shiqi，Chi Xu，Ming Xie.A Robust O(n)Solution to the Perspective-n-Point Problem［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2012，34(7):1444-1450.

［16］Quan L，Lan Z.Quan and Z.Lan，Linear n-Point Camera Pose Determination［J］.IEEETrans.Pattern Analysis and Machine Intelligence，1999，21(8):774-780.

［17］Umeyama S.Least-squares estimation of transformation parameters between two point patterns［J］.IEEE Transactions onPattern Analysis and Machine Intelligence，1991，13(4):376-380.