Stirling公式的進一步拓展

張麗穎

(健雄職業技術學院軟件與服務外包學院，江蘇太倉215411)

詹姆斯·斯特林(James Stirling)于1730年給出了:n!～C·n(n+12)·e－n，并求出了近些年，Stirling公式還多次被推廣．其研究不斷地深入．

1999年，徐利治［1］給出了n!的二重級數表達式并推出其雙邊不等式為

2004年，匡繼昌［2］對Stirling公式做了進一步推演:

并指出，經常使用的n!近似估計式有:

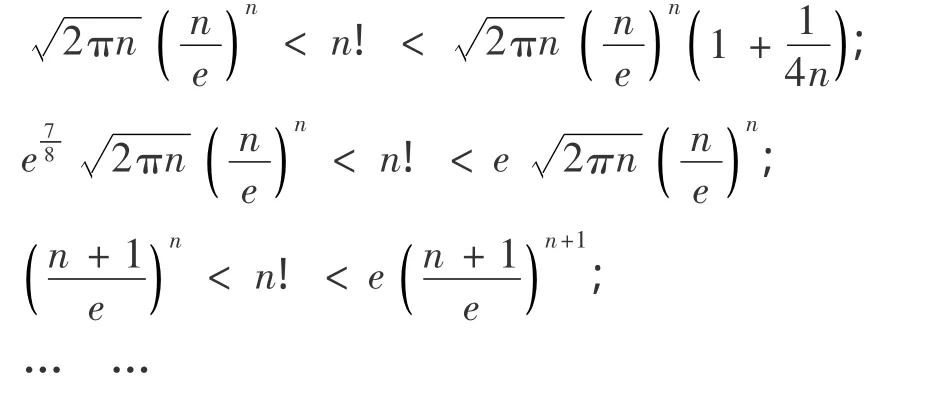
文獻［3］、［5］、［6］也對 Stirling公式進行了論證:

在文獻［3］中還有如下結果為

在文獻［4］中有如下結果:

kk函數的最大值．

將Stirling公式再進一步拓展，以期得到等差數列乘積的數值逼近表達式．

1 等差數列乘積的數值逼近

首先把Stirling公式中的自然數乘積n!=1·2…n拓展為等差數列乘積:

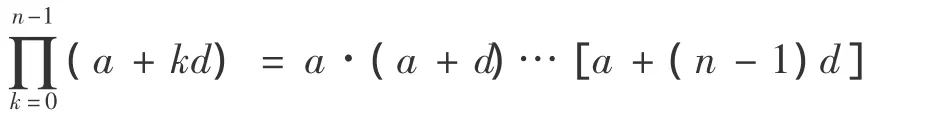
1．1 等差數列乘積的表達式

定理1 設a ＞0，d ＞0，n∈N*，則:

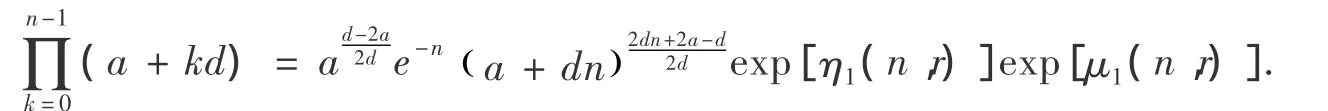
其中:

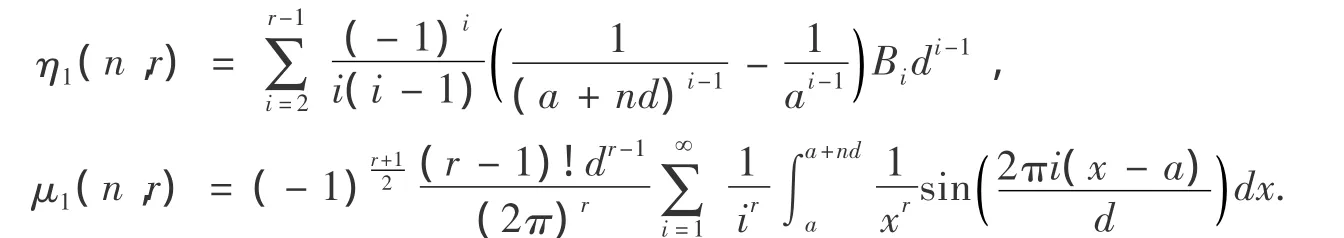
證明:根據Euler-Marclaurin公式，又由f(x)=ln x的n階導數:

在［a，+∞)是絕對連續的，再取t=0，h=d，b=a+nd，又根據Bernoulli函數性質中的Bk(0)=)，Bernoulli數中的 B2k+1=0，則取 r為某一奇數，有Br(0)=0．可得:

分別對(2)中的3個表達式變形得:

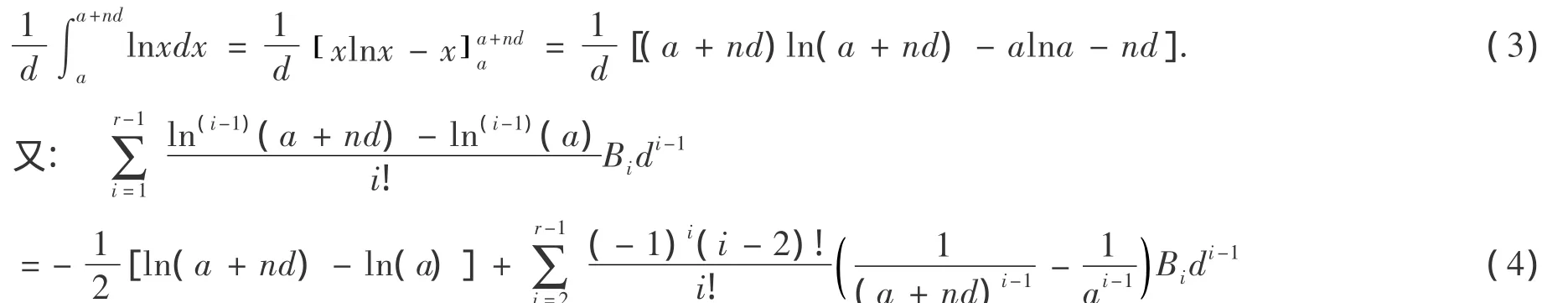
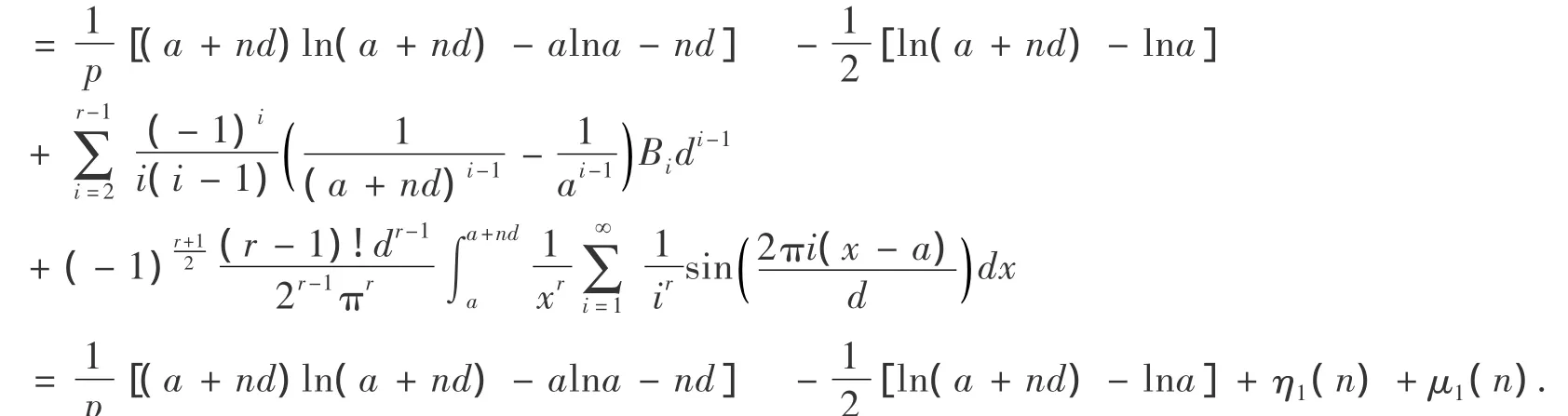
即證:

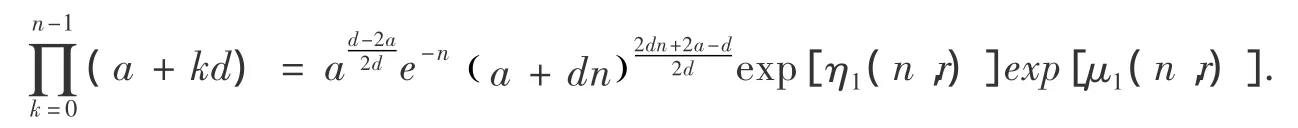
由于μ1(n)含有積分式，需要簡化，有下面結果．可以作為當等差數列乘積的近似表達式的一個誤差估計．

證明:

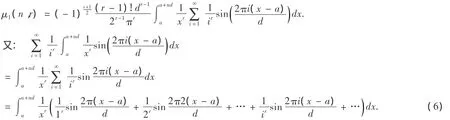
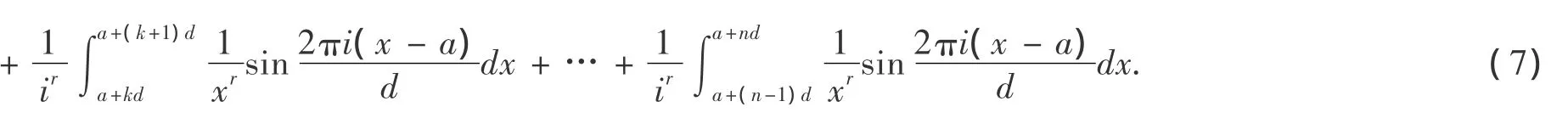
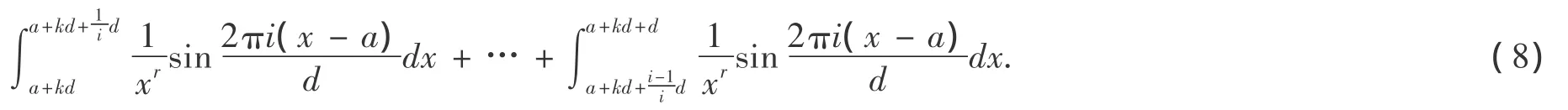
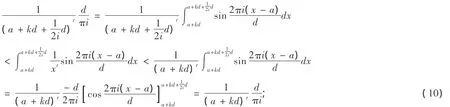
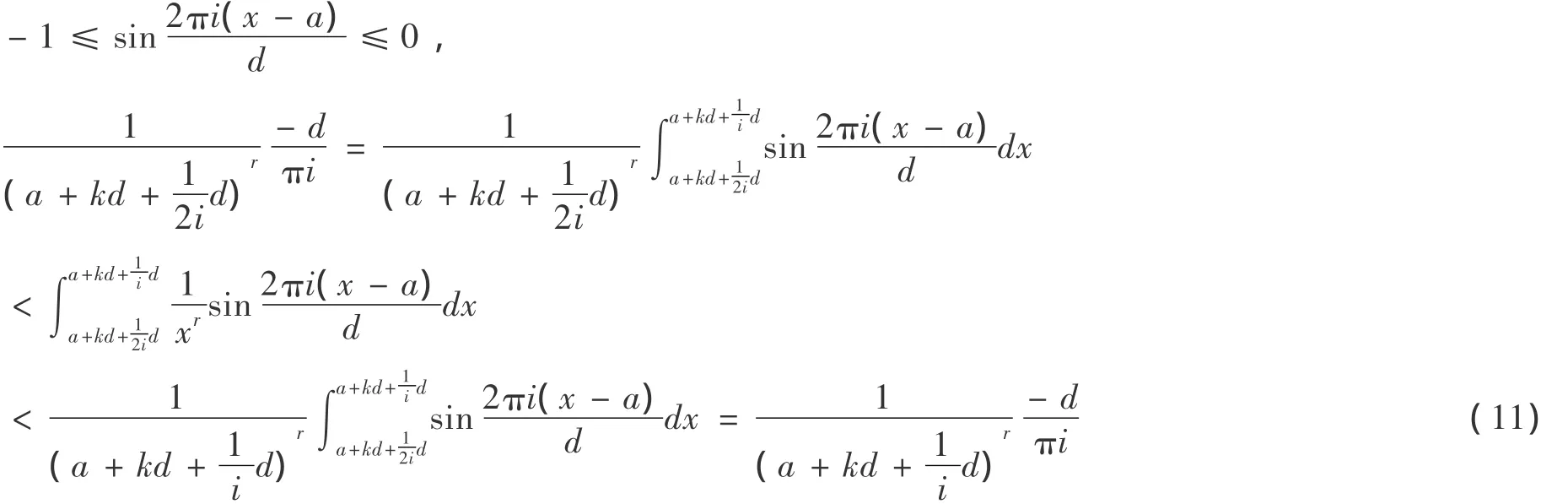
將(10)，(11)代入(9)得:

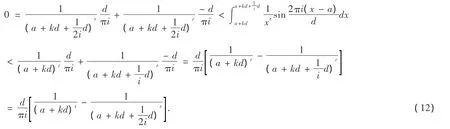
同理，依次可以推得i個不等式，最后一個為:

將(12)(13)等i個不等式相加得:

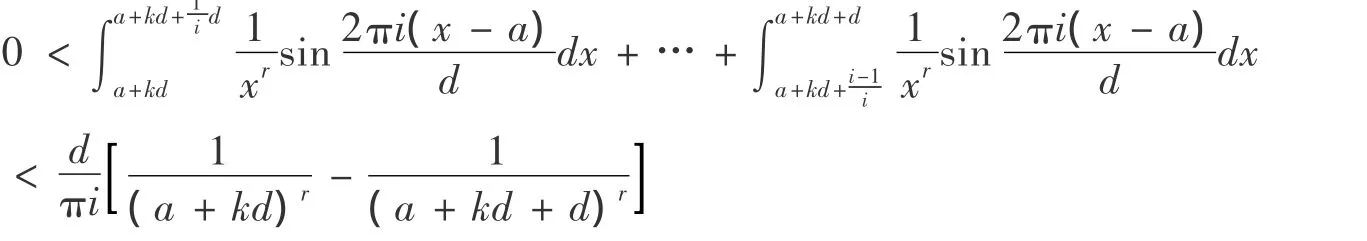
由(7)，對(14)中k相加，得:

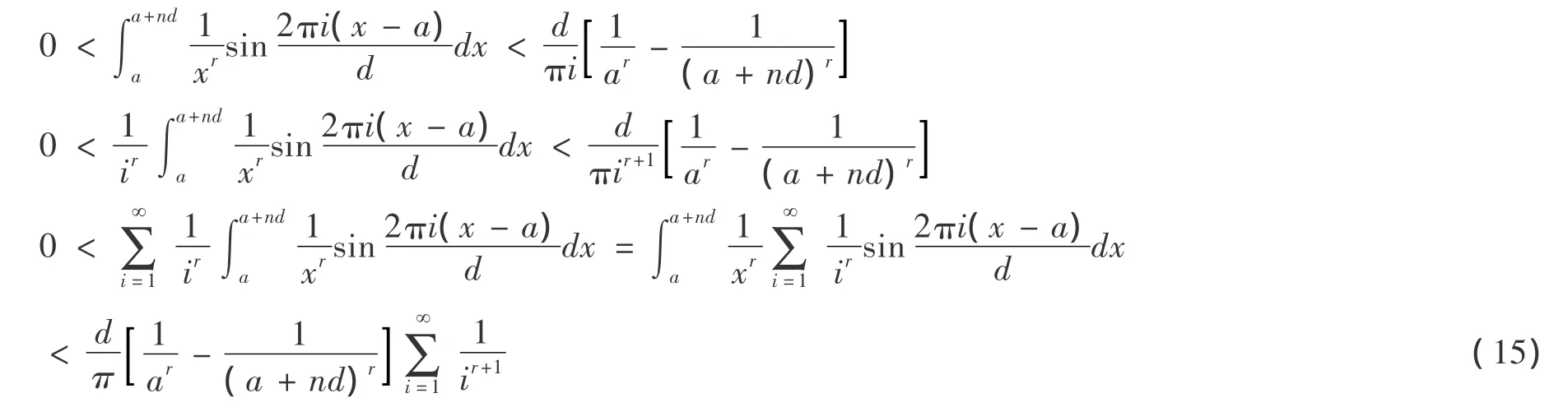
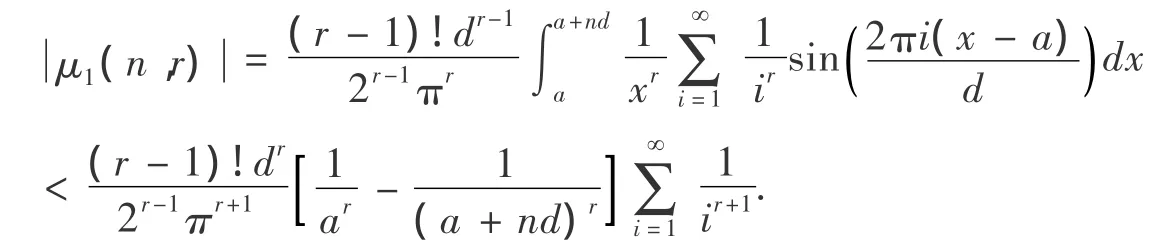
1．2 相關推論

為了將定理1的公式變成另一簡潔形式．有下面推論1．

推論1 設a ＞0，d ＞0，n∈N*，則:

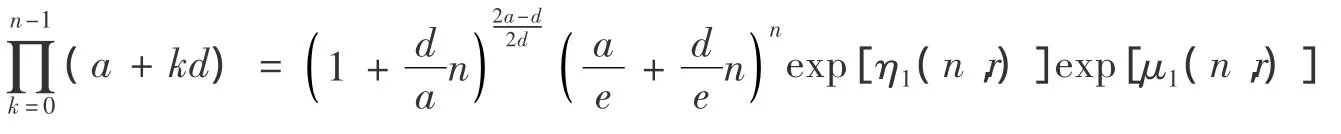
推論2 設a ＞0，d ＞0，n∈N*，則:

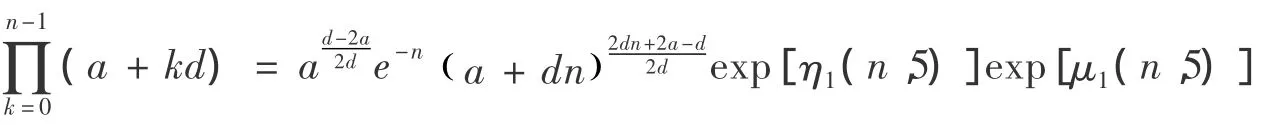
證明:在定理1，2．2 中，對于:

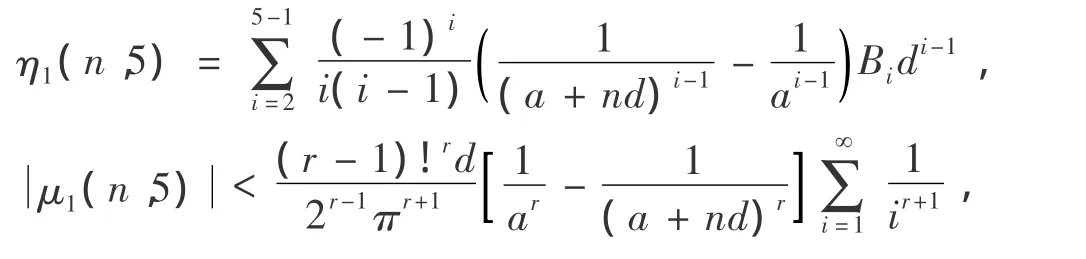
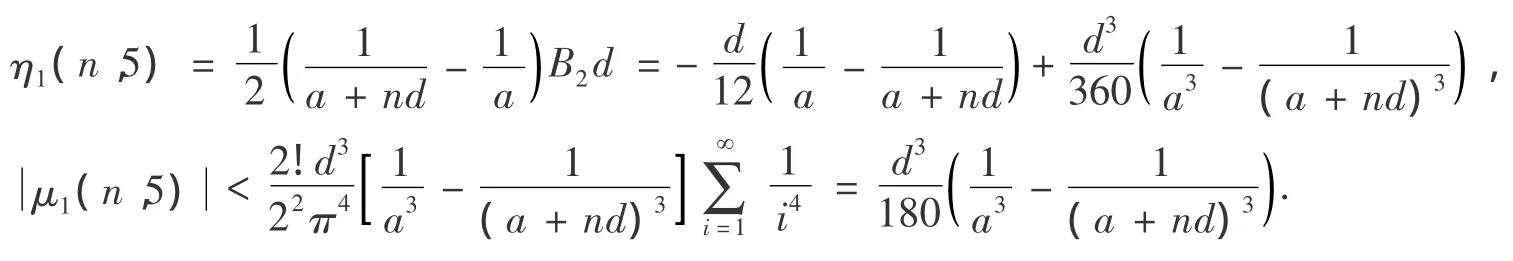
由定理2推導過程的(15)，r=5，下式:

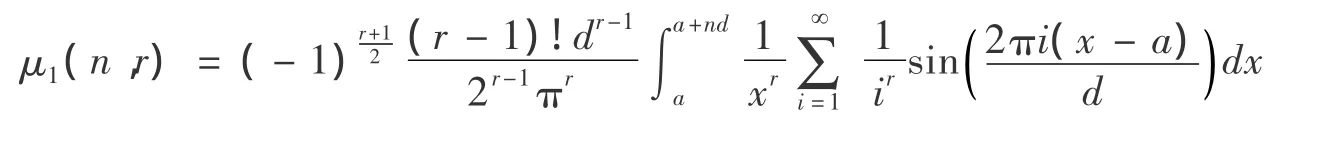
推論3設a ＞0，d ＞0，n∈N*，則:

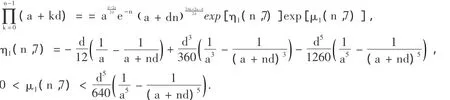
有關a，d可取整數之外的其它任意正數，比如是小數或無理數，會得到大量代數式，其例子不再列舉．

因此，定理1推廣了n!估計式，拓展了Stirling公式的應用范圍．

2 數值逼近表達式的實例檢驗

對于推論3的數值逼近的精度，采用數學……