基于貨幣時間價值表的時間軸運用研究

安陽師范學院 陳 艷

貨幣時間價值是指貨幣隨著時間的推移而產生的價值增值，時間越長，增值越多。貨幣時間價值的表現形式有多種：如果是一次性投入的款項，按照計息方式，有單利和復利之分，其中單利只對本金計息，而復利對本金所產生的利息也要計息；如果是定期等額收付款項，就是年金，按照收付的時間點，可進一步分為普通年金、預付年金、遞延年金和永續年金，其中普通年金是指從第一年開始，每年年末等額收付的年金形式，而預付年金則是從第一年開始，每年年初等額收付的年金，遞延年金的第一次收付點不是第一年，永續年金沒有到期日。在多種貨幣時間價值的表現形式中，單利比復利的運算簡單，應用較少，而年金中，普通年金是其它年金的基礎，所以，貨幣時間價值的研究重點在復利和普通年金上。

為了輔助貨幣時間價值的計算，就出現了貨幣時間價值表。貨幣時間價值表一般有四個，即一元復利終值表、一元復利現值表、一元年金終值表和一元年金現值表。其中，終值是指現在一定量的資金在未來某一時點上的價值，而現值是指對未來的現金收付按照一定的折現率進行折現后的現在價值。現筆者以10%的折現率為例列出其在若干期的四個系數表的相關數據。

表1 折現率i=10%時的貨幣時間價值表

初學貨幣時間價值，往往先要接觸這樣的貨幣時間價值表。對于這個表的查法，經過簡單的學習，一般都能快速地掌握。可是，對于表中各個數據的含義以及數據間的內在聯系，往往缺乏研究，也很難掌握。如果能夠通過一定的方法簡單快速地掌握貨幣時間價值表中的數據，對于貨幣時間價值的深入了解和靈活運用將會有很大的幫助。

一、貨幣時間價值表中時間軸的運用

時間軸是研究貨幣時間價值的必要手段和輔助工具。圖1是一個簡單的時間軸，在此軸中，起點0表示第一年年初，終點n表示第n年年末，除此兩點之外，其他的時間點都有兩個含義，既表示該年年末，又表示下年年初。如，時間點1即是第一年年末，又是第二年年初。

圖1 時間軸

運用時間軸，能夠將貨幣時間價值表中的數據表示在這條軸上。下面把表1中折現率為10%，期數為第10期的四個數據分別表示在相應的時間軸中。

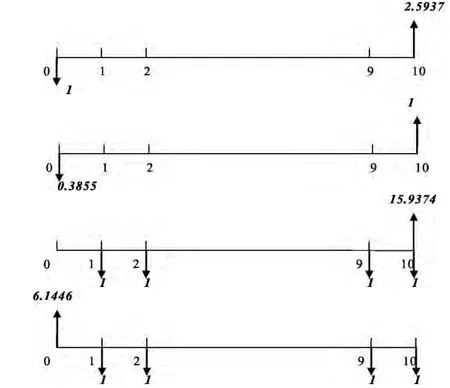
圖2 折現率為10%，期數為10期的時間軸

以上四條時間軸中，第一條時間軸是當折現率i=10%，期數n=10時的復利終值系數，其中2.5937的含義是指“如果在第一年年初投入1元錢，在年復利率為10%，每年復利一次的情況下，到第十年年末的本利和就是2.5937元”。

第二條時間軸是當折現率i=10%，期數n=10時的復利現值系數，其中0.3855的含義是指“如果想十年后的本利和達到1元錢，在年復利率為10%，每年復利一次的情況下，第一年年初要投入0.3855元”。

第三條時間軸是當折現率i=10%，期數n=10時的年金終值系數，其中15.9374的含義是指“如果從第一年開始，每年年末投入1元錢，共投入十年，在年復利率為10%，每年復利一次的情況下，到第十年年末的本利和就是15.9374元”。

第四條時間軸是當折現率i=10%，期數n=10時的年金現值系數，其中6.1446的含義是指“如果從第一年開始，每年年末投入1元錢，共投入十年，在年復利率為10%，每年復利一次的情況下，折現到第一年年初就是6.1446元”。

通過時間軸，了解了貨幣時間價值表中每個數據的含義，下一步就要研究這些數據之間的內在聯系了。

二、貨幣時間價值表中各數據的關系

（一）復利終值與現值的關系 從圖2中前兩條時間軸上可以看出，第一年年初的1元錢到第十年年末就成了2.5937元，那么，如果十年后要有1元錢，第一年年初就要投入1/2.5937元，而這個結果正好就是0.3855元。所以說，復利終值與現值互為倒數關系。

（二）年金終值與現值的關系 在圖2的后兩條時間軸上，從第一年開始，每年年末投入1元錢，共十年，折算到第十年年末就是15.9374元，而折現到第一年年初則是6.1446元。這里的15.9374和6.1446的關系其實就是分別互為終值和現值，即：15.9374×（P/F,10%,10）=15.9374×0.3855≈6.1446；6.1446×（F/P,10%,10）=6.1446×2.5937≈15.9374。

（三）復利與年金的關系（1）復利終值與年金終值的關系。圖2中第三條時間軸是10年期的年金終值系數，從圖中可看出它等于從第1點到第10點各點投入1元錢的復利終值之和，而在第一條復利終值時間軸中，10年期的復利終值系數的資金投入點是在0點。這就說明，年金終值系數應該是從9年期到8年期，一直到0年期各期復利終值系數之和，即15.9374=2.3579+2.1436+1.9487+1.7716+1.6105+1.4641+1.3310+1.2100+1.1000+1。

（2）復利現值與年金現值的關系。圖2中第四條時間軸是10年期的年金現值系數，從圖中可看出它等于從第1點到第10點各點投入1元錢的復利現值之和，而在第二條復利現值時間軸中，10年期的復利現值系數的1元錢所在的點是在第10點。這就說明，年金現值系數應該是從10年期到9年期，一直到1年期各期復利現值系數之和，即6.1446=0.3855+0.4241+0.4665+0.5132+0.5645+0.6209+0.6830+0.7513+0.8264+0.9091。

（四）普通年金與預付年金的關系 預付年金是指發生在每期期初的等額收付款項，相對于發生在每期期末的等額收付款項普通年金而言，無論是終值還是現值，都是多計了一期的利息。所以預付年金終值=（F/A，i，n）×（1+i），預付年金現值=（P/A，i，n）×（1+i）。如果查年金系數表的話，預付年金終值系數應該在普通年金終值的基礎上，期數加1，整體系數再減1得到；而預付年金現值系數應該在普通年金現值的基礎上，期數減1，整體系數再加1得到。比如說，要得到折現率為10%，期數為10期的預付年金終值，要先查期數為11期的年金終值系數，找到18.5312，再減去1得到17.5312；要得到折現率為10%，期數為10期的預付年金現值，要先查期數為9期的年金現值系數，找到5.7590，再加上1得到6.7590。

三、以時間軸反映數據之間的關系

（一）正負時間軸的運用——反映互為倒數關系的數據 對于時間軸，常見的都是正的時間軸，下面筆者引入一種負的時間軸，如下圖3所示。

圖3 負時間軸

在圖3中，起點-n表示前n年的年末，終點0表示去年的年末，同時也是今年的年初，也就是現在所處的時間點，其他的時間點都有兩個含義，一是表示前1年的年末，二是表示該年的年初。比如說，時間點1即是前年的年末，又是去年的年初。

通過負時間軸和正時間軸的結合形成的綜合時間軸，就能夠在一條軸上同時反映出互為倒數關系的數據。在貨幣時間價值體系中，互為倒數關系的數據一共有三對，除了前文提到的復利終值和復利現值互為倒數外，年金終值系數與年償債基金系數、年金現值系數與年資本回收系數也互為倒數關系。下面筆者還是以折現率為10%，期數為10期的情況，列出三條正負時間軸來表示三組互為倒數的數據，如下圖4、5、6所示。

圖4 折現率為10%時的復利現值系數和復利終值系數

圖4中，如果前十年年末投入0.3855元，在年復利率為10%的情況下，到今年年初，本利和就達到了1元錢；今年年初的1元錢，在年復利率為10%的情況下，到第10年年末，本利和就是2.5937元。其中的0.3855和2.5937分別是復利現值系數和復利終值系數，兩者互為倒數。

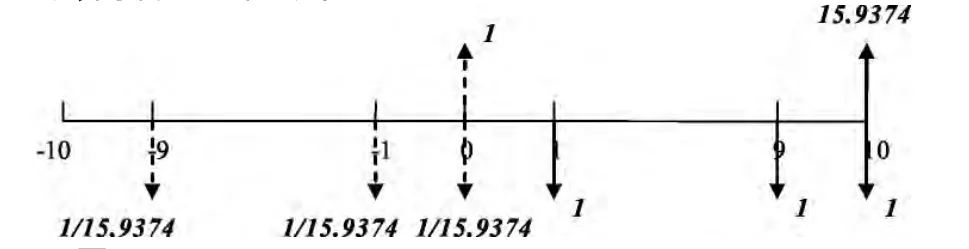
圖5 折現率為10%時的年償債基金系數和年金終值系數

圖5中，如果從前10年的年初開始，每年年初投入1/15.9374元，連續10年，一直到今年年初，在年復利率為10%的情況下，到今年年初，本利和為1元錢；從今年年末開始，每年年末投入1元錢，連續10年，一直到第10年年末，在年復利率為10%的情況下，到第10年年末的本利和為15.9374元。其中的1/15.9374和15.9374分別是年償債基金系數和年金終值系數，兩者互為倒數。

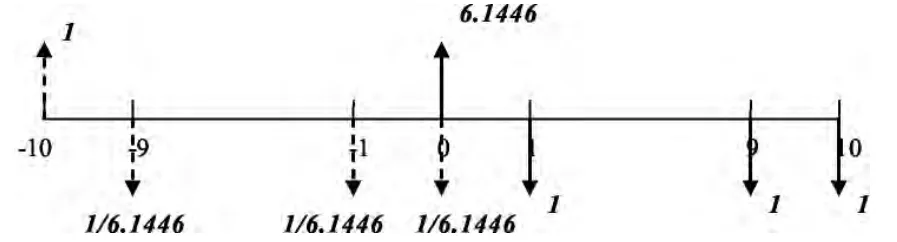
圖6 折現率為10%時的年資本回收系數和年金現值系數

圖6中，如果從前10年的年初開始，每年年初投入1/6.1446元，連續10年，一直到今年年初，在年復利率為10%的情況下，折現到前10年年末，就是1元；從今年年末開始，每年年末投入1元錢，連續10年，一直到第10年年末，在年復利率為10%的情況下，折現到今年年初就是6.1446元。其中的1/6.1446和6.1446分別是年資本回收系數和年金現值系數，兩者互為倒數。

通過以上3個正負時間軸，就把三種互為倒數關系的數據以及他們之間的換算關系完整地反映在一起了。

（二）綜合時間軸的運用——反映互為現值和終值關系的數據 貨幣時間價值體系中，互為現值和終值關系的數據有兩對：普通年金現值與終值、預付年金現值與終值。可以在一條時間軸上反映出兩者的關系來，如下圖7、8所示。

圖7 普通年金現值系數與終值系數

圖7中，從第1年開始，每年年末投入1元錢，連續10年，在年復利率為10%的情況下，到第10年年末，本利和達到15.9374元；如果折現到第1年年初的話，則是6.1446元。從時間軸上可以看出，15.9374在第10點，6.1446在0點，兩者剛好就是終值和現值的關系。

圖8 預付年金現值系數與終值系數

圖8中，從第1年開始，每年年初投入1元錢，連續10年，在年復利率為10%的情況下，到第10年年末，本利和達到17.5312元；如果折現到第1年年初的話，則是6.7590元。從時間軸上可以看出，17.5312在第10點，6.7590在0點，兩者也是終值和現值的關系。

（三）綜合時間軸的運用——反映普通年金與預付年金的關系 無論是預付年金終值還是現值，都是在普通年金終值和現值的基礎上多計了1期利息，同樣也可以在同一條時間軸上反映出這個聯系，如下圖9、10所示。

圖9 普通年金終值系數與預付年金終值系數

在圖9中，10個1元錢的資金投入點是一樣的，都是從1到10十個點，折現率也一樣，都是10%，但是，由于代表的含義不一樣，就會在不同的點產生不同的終值。如果把這十個點看作是每年年末，亦即從第1年年末開始，一直到第10年末為止，這就是普通年金，到第10年年末，普通年金的終值就是在第10點的15.9374元；如果把這十個點看作是每年年初，亦即從第2年年初開始，一直到第11年初為止，這就是預付年金，到第11年年末，預付年金的終值就是在第11點的17.5312元。從時間軸上看，15.9374與17.5312剛好相差一期，兩者的關系是15.9374×（1+10%）=17.5312。

圖10 普通年金現值系數與預付年金現值系數

在圖10中，10個1元錢的資金投入點是一樣的，都是從1到10十個點，折現率也一樣，都是10%，但也是由于代表的含義不一樣，就會在不同的點產生不同的現值。如果把這十個點看作是每年年末，亦即從第1年年末開始，一直到第10年末為止，這就是普通年金，折現到第1年年初，普通年金的現值就是在第0點的6.1446元；如果把這十個點看作是每年年初，亦即從第2年年初開始，一直到第11年初為止，這就是預付年金，折現到第2年年初，預付年金的現值就是在第1點的6.7590元。從時間軸上看，6.1446與6.7590剛好相差一期，兩者的關系是6.1446×（1+10%）=6.7590。

通過以上的分析，如果能夠巧妙運用時間軸，就能夠把復雜的貨幣時間價值表中的數據以及數據之間的關系體現在一條條簡單的線段上，達到化繁為簡的效果。

［1］毛付根：《管理會計》，高等教育出版社2007年版。