數學人類學：一個新的研究動向

張和平，徐曉光，羅永超

（凱里學院，貴州 凱里 556011）

數學人類學，是認知人類學的一個分支.國際人類學與民族學聯合會（IUAES）下設有27個研究委員會（2004年），數學人類學委員會是其中之一[1].然而，在中國學術界卻沒有開展數學人類學研究.這里簡述中國學者近幾年來研究各民族數學文化的現狀，分析當前對民族數學文化研究概念的糾結原因，引介歐美國家數學人類學研究理論，并介紹凱里學院研究團隊從“民族數學”走向“數學人類學”的研究實踐，以及對數學人類學研究工作的思考.

1 中國學者研究各民族數學文化的現狀

關于中國少數民族數學文化，在20世紀90年代，就有周開瑞、呂傳漢、代欽等教授分別對羌族、水族、蒙古族等作了積極的探索，并搜集得到一些成果.

內蒙古師范大學代欽教授研究蒙古族傳統生活中的數學文化發現[2]，蒙古族傳統建筑——蒙古包具有黃金比例（即約為0.618）結構.哈那高與椽子長之比約為0.625，柱高與底基直徑之比是0.611 2.古代，蒙古族計算方法都體現在古經《珠露海》中.其“縱橫圖”（圖1）對數學計算和數字有很大影響.縱橫圖及其9個數字在蒙古族傳統生活中是非常重要的，9個數字有著宗教、哲學方面的意義.在占卜時，給縱橫圖中的9個數字賦予與人的命運等有關的具體內容，然后，使每個數字與連續的12年相對應，于是9個數字與108年相對應；還有一種算法，使9個數字與八卦對應，即過“縱橫圖”中心數字的3個數字和與之相反的兩個方向對應.這樣就完全確定了縱橫圖與八卦的關系.還有一些圖案藝術和服飾制作也符合數學的簡單、對稱、和諧等美學標準.

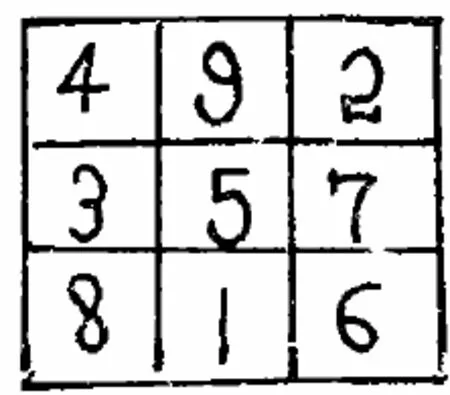
圖1 縱橫圖

西南民族大學周開瑞教授對羌族數學的形成進行了初步的搜集與整理[3].內容包括整數的概念及運算，幾何圖形，以及建筑和日常生活中的數學應用.他研究發現，羌族記數工具是一條硬質圓木棍，在其上刻一道圓弧表示個位“1”，刻一道圓圈表示“11”.例如甲向乙借了32元，就在木棍上刻三道圓圈兩道圓弧（圖2）.當場把圓木從中劈為二，各持一半，相互合并，刻痕必須完全吻合，方知借貸數目分毫不差.羌族人民有4種計量長度單位，分別是“卡”、“步”、“排”、“繩”等，并且還發現有換算關系：1繩=12排，1排=2.5步=10卡，1步=4卡，等.

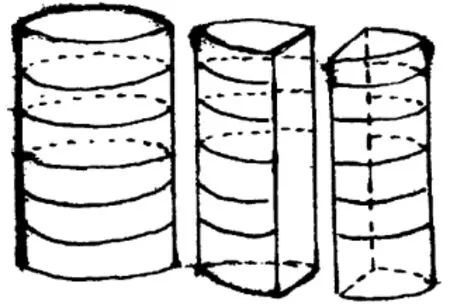
圖2 硬質圓木棍刻痕計數

在這些前輩學者們研究工作的影響下，21世紀初，相繼有羅永超、肖紹菊和周長軍等教授以及一些青年學者也參與了少數民族數學文化的搜集與研究.

凱里學院羅永超教授主要研究侗族數學文化[4]，他發現侗族的自然數中最大的計數單位是“千萬”，“千萬”以下的計數單位與現代數學相同，最小的自然數是1，在侗族母語中沒有零（僅用“無”或“完”表達其意）和負數的讀法；有分數和小數的概念和意義，但表達不了純小數.沒有無理數等概念.幾何概念較為豐富，如三角形、多邊形、圓、直線、平面等在侗族母語中都有，但抽象程度不高，遠未達到“數學化”的水平，很多概念含混不清.侗族人民能巧妙地運用了2和及10的倍數將乘法較好地轉化為加減法的運算，可以克服沒有“九九表”的困難[5].肖紹菊教授研究苗族服飾中的數學元素發現[6]，苗族人民崇拜圖騰和數字，在重大的祭祀活動中“9”、“11”使用得最多，體現其威嚴性和莊重性.在服飾中的幾何紋有如三角形、正方形、長方形、平行四邊形、五邊形、六邊形、菱形、圓、螺旋線、星形線、玫瑰線等圖形.這些最基本的圖形通過連接、對稱、組合又構成了較復雜的紋樣，如太陽紋、鋸齒紋、菱形八角花紋、回紋、水波紋、卷蔓紋、牛角紋、魚紋、蝶紋、龍紋等[7].

在搜集、整理苗族數理文化時發現[8]，苗族生活中已經形成基本的基數、序數的概念，并且進行簡單的加、減和成倍的運算；有行之有效的簡單的度量衡，包括長度、重量、面積和體積等.苗族所用的長度單位主要有doud（拳）、diud（拤）、dlingx（庹）、dlob（步）等，與現代漢語用的測量單位不一樣，這可能跟苗族所用的測量工具主要是來源于他們的身體肢體部位如手、腳等有關.苗族在宗教的“nux（占卜）”活動中，還運用概率和統計的相關基礎知識，形成統一規范的解決一類問題的思維決策數學模型[9].

周長軍教授帶領的課題組，對云南德宏傣族文化中的數學因素調查發現[10]，傣族有簡單的記數和初級的算術加減法運算；度量單位有“liu43（指）”、“xwp43（拃）”、“skl1（肘）”、“wa53（排）”等，傣族對幾何的認識，主要從生產、生活中對幾何圖形的應用上表現出來.關于多邊形，傣族是以角來定義的，稱為三角形（ha33 sam35 tse11）、四角形（ha33 si11 tse11）、多角形（ha33 tse11 lǎm35）等，但沒有進行細分.傣族對幾何圖形沒有系統概括出性質、精確的計算公式、幾何命題的邏輯推理，只處于實用階段[11].王奮平、陳穎樹兩位教授對黎族數學文化研究也發現[12]，海南黎族在長期生產、生活中總結出很多簡單而原始的數學知識，基數詞只有1到100，有加、減、乘運算，沒有除法運算.記數主要是實物記數、借物記數、刻木記數.常以“一柞”、“一庹”、“一步”、“一歇”和“一日”等作為度量單位.在黎錦圖案、紋面圖案等中體現出對幾何知識的應用.

此外，青年學者劉超、張茜對新疆哈薩克族數學文化進行了調查[13].他們搜集、整理哈薩克族運用的基數、序數及其運算，數的進制，數字文化與數字崇拜，度量衡、歷法、幾何知識等.他們認為，隨著地方經濟的快速發展以及主流文化的影響，少數民族的傳統文化遺產（包括各民族的數學文化）受到了空前的沖擊，以致瀕臨滅亡.對這些堪稱“人類社會發展史活標本”的搜集、整理，其意義和價值并不亞于對一種瀕危物種的保護.

綜上所述，關于中國少數民族數學文化研究，自20世紀90年代開始，中國學者主要是對蒙古族、苗族、哈薩克族、羌族、黎族、侗族、傣族等的數學文化開展搜集與整理.從研究成果中可以看出，各個民族聚居區域發現和形成的數學文化有共通之處，或相似的地方，例如各個民族使用的基數、序數以及簡單的運算，蒙古族和侗族的建筑運用黃金分割數，苗族、哈薩克族、傣族、黎族等使用的度量衡如“一柞”、“一庹”、“一步”等.這些都是人類建構的工具、智慧的結晶，是他們“基于生活形式上的約定，是公共性質的”[14].

2 當前中國學者對民族數學研究的糾結以及數學人類學的引入

上述中國學者對不同地域、不同民族的數學文化探索，取得一系列的成果.然而，有一個問題是不可回避的，那就是“研究什么”的問題，是一個研究對象問題.正如此，使得研究存在諸多詰難.分析當前研究情況，存在兩種不同的說法：“民族數學”說和“數學人類學”說.

2.1 “民族數學”說

叫做“民族數學”嗎？這個概念就是當前中國一些研究者比較認同的一種說法，也是常常使用的一個概念.這個叫法也是有根據的.

“民族數學”這個詞，在1984年8月第五屆國際數學教育大會（ICME-5）上提出來，英文為Ethnomathematics.在數學家、人類學家、心理學家和教育家中，懷爾得（R L.Wilder）、懷特（L.White）、費得沃斯（Fettweis）、盧可特（Luquet）和雷姆（Raum）等被認為是民族數學研究的先驅.其他教育家、數學家、人類學家和哲學家也逐漸地加入到費得沃斯、懷爾得、盧可特等早期的民族數學思考之列.“民族數學”一詞提出后，對概念的界定也不一.巴西數學史家達布羅西歐（Ubiratan Ambrosio）認為，“民族數學”是指個人在不同文化與環境脈絡中，適應與解釋實體世界的不同方式.并將民族數學作為不同的文化系統中“跟蹤與分析數學知識產生、傳播、擴散并標準化過程的方法”[15].這個定義明確了民族數學概念的“地域性”、不同民族的“文化背景差異”以及解決“實體世界”問題的“不同方式”，體現了“數學”的主體地位和“民族”差異的修飾作用[16].美國數學家懷爾得在其出版的《作為文化體系的數學》一書中指出，數學作為一種文化，在各個不同的文化體系會產生不同的數學，民族民間中的典型文化諸如哲學、宗教、習俗、藝術、社會環境等都對數學的產生和發展起到約束作用.民族數學的研究，首要的是對民族文化的研究，對民族學生的文化意識的研究[17].呂傳漢教授和汪秉彝教授對“民族數學文化”做出這樣的界定，民族數學文化可以理解為存在于民族文化群落里的數學思維模式及其系統實踐的知識綜合[18].換句話說，民族數學是存在于特定文化群體中的數學思想和數學活動，是一種情境性的數學[19].據此，當前中國學者對各個少數民族聚居區的數學文化搜集與研究，認為就是“民族數學”研究.但有些學者卻認為“民族數學”說法不妥當.他們批駁難道：還有“民族物理”、“民族化學”嗎？這些問題已是一個糾結.

2.2 “數學人類學”說 即歐美數學人類學研究引介

數學人類學委員會是國際人類學與民族學聯合會（簡稱IUAES）的27個研究委員會（2004年統計）之一，在歐美等西方國家從20世紀60、70年代開始就開展數學人類學的研究.下面對歐美國家的數學人類學理論和研究做簡要介紹[16].

國際人類學與民族學聯合會數學人類學委員會主席、美國夏威夷大學保羅·W·迪克森（Paul W.Dixon）教授認為，“在數學知識中，有一種既是文化又是神經生理的來源.數學知識的基礎作用在所有人類文化中顯示出來……數學理解力在信息時代、現代電腦和因特網的控制論中存在著更大的價值.”并且還認為“數學人類學委員會將在21世紀繼續致力于這一迫切需求的研究.”[20]在《數學的文化適應：數學教育的文化視角》（Mathematical Enculturation: a Cultural Perspective on Mathematical Education）一書中，比斯霍普（Alan J.Bishop）結合數學和人類學這兩門學科特點，創造性地提出一個重要的觀點：在今天的文化背景下，人類學是理解數學知識傳播的一個有用工具[21].

數學人類學家漢斯霍夫曼（Hans Hoffman）教授在文章《數學人類學》（Mathematical Anthropology, 1969）中對數學人類學的價值、對象做剖析[22].文章指出，盡管人類的想象力是無拘無束，不受制約，但是個人的經歷是有限的.經歷有賴于工具，并且能發展成獨創想象力的廣泛領域.我們能夠想象不同物體的尺度，但是需要一種工具——自然數——來驗證它們.出于這個原因，工具是文化的實質；無論是在物質上還是精神上，它們允許人類體驗世界廣闊的萬物.梭標投射器允許人類早期體驗猛犸象的肉，而不用別的相反的方法.……數學是一種工具，在物質世界中能使人類理解和控制巨大數量的事件和工序.特別是，數學是一個工具，滲入想象的領域，徹底地超越一個沒有思想工具的經歷.而且，一旦數學工具已經被開發，它們經常改變它們的效應和擴大不僅是一個經驗，并且還有一個人的想象力.……就像所有的人類文化一樣，數學是在不斷地發展.早期創造者開發的工具（或問題解決的方案）是被壓縮、廣義和存儲，成為今天人類文化的庫存.……幾何學收集埃及人的測量規律，希臘人的演繹過程，非歐幾里得形式化表示和超越局限三維空間的運動，并且利用它們為一般的太空探索建造一個工具.……數學和科學是非常不同的系統，也許如同男人和女人的不同一樣.然而，它們的結合是已經被證實為多產.使用數學方法分析從實踐中獲取的數據是科學的原本（真實，標準）.相對應，從實踐中獲得的問題又能激發很多數學創新.……事實上，人類學是處理人、事件、工件、情感、血緣關系和許多其它的現實現象.在各種非凡的數據中，人類學也許是科學規律特有的.它超出被動思考得到的數據，然而，盡管許多人類學家都被吸引到他們的領域，由一個直覺和情感卷入異域風情之中.人類學是一門科學，目的是調查事件、親屬條件等的實際結構；但也是對當地的人和他們的生活的一種認識，指與其他人交流的生活.如果沒有別的原因，一個人類學家的感情卷入他的數據應該是確定的.然而，對于開發解釋各種數學結構是最有效的工具，并且是最自然的語言，能把個體經驗帶進廣大聽眾的世界.數學并非是破壞直覺；相反，它是用一種通俗易懂的形式傳遞直覺.……由于數學理論已經進化成為歐美的概念工具，并非所有已知的數學知識把易洛魁人、奧馬哈人和其他親屬關系結構化.在親屬關系學中建構同構或同態模型，傳統的數學可能沒有用.如果如此，那么對于人類學——特別是數學，它的許多現存基礎可能更有用（e.g., Romney and D’ Andrade,1964; Lamb, 1965: 56; Hammel, 1965）.另一方面，親屬關系可能不被認可作為數學函數來研究.在這種情況下，一個正式識別的、合適類別的數學映射將是一個能進一步分析的有用工具.

加利福尼亞大學的數學人類學家米奇爾巴頓（Michael L.Burton）教授在同個題目的文章《數學人類學》（Mathematical Anthropology）[23]中，他選擇了懷特（D.R.White）[24]和漢斯霍夫曼（Hans Hoffman）沒有研究的論題（在人類學的領域），對“人類學中的度量模式”（Measurement Models in Anthropology）、“度量的目標”（Goals of Measurement）、“數據的近似度量”（Similarity Measures for Nominal data）以及“優選法或排隊法的模型”（Models of Preference or Rank Ordering）、“多維模型”（the Multidimensional Model）等開展研究.認為，在人類學中測量問題是無處不在的.人類學中測量的焦點問題是文化演變的研究，包括語義學模式、社會組織變化的度量，概率論（馬爾可夫過程等）應用于人口理論和種群理論.如離婚率或結婚習俗.距離測量既是直線也包括多維空間，如三角不等式：

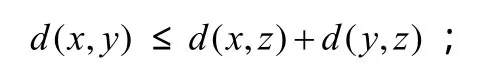
歐幾里得距離公式：

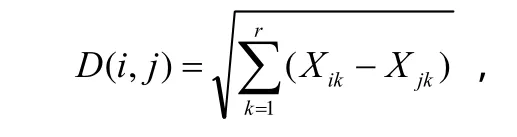
即是畢達哥拉斯定理的一般化形式.在空間中描繪點是文化對象的各種形式，例如言語、信仰、文句和種族，或個體角色.在人類學中關于做三維數學研究最近取得了一些成就，這說明只要改進人類學中模型框架就能體現來自其它數學社會科學的有效性.

巴羅諾夫（Ballonoff）和鮑爾A（Paul A.）在《社會人類學的數學基礎》一文中，提出了一個綜合數學理論，對社會人類學和其必然聯系的地區人口理論，包括人口和遺傳的措施.例如，從一個簡單的社會“婚姻規則”傳統習俗，可以計算人口統計數據的穩態或“零增長”.并且數據統計揭示“現代”和“原始”的內涵.

英國數學人類學家托馬斯·克倫普專著《數字人類學》[25]，是世界第一本系統的數字人類學著作，采用了世界各地大量的歷史資料和田野調查數據，提供了關于數字在文化中使用的第一手材料，涉及了法、德、拉丁、希臘、日、中、梵等多語種，有不同人類族群，包括“數字與語言”、“測量、比較”、“數字在建筑中的應用”、“數字文化：傳統與現代”以及“數字習俗的傳播與地方性文化”等內容.

美國數學家懷爾得（R L.Wilder）1981年從數學人類學的角度提出了“數學——一種文化體系”的數學哲學觀.科諾爾斯（Jeanne Connors）在文章《數學與人類學的交流：學科間對話的需求》（When Mathematics Meets Anthropology: the Need for Interdisciplinary Dialogue）中認為，人類學領域太缺乏（數學）教育研究領域，不管在最近的出版書還是在較晚的論文中，關于文化背景下的數學教育應用人類學方法探討數學文化，這是值得振奮的事情.

數學哲學家維特根斯坦教授認為，數學僅僅是基于生活形式上的約定，是具有公共性質的.數學計算只不過是語言游戲活動，而語言游戲之所以能進行下去，是因為它是基于生活形式的一致性，這顯然脫離不了各種社會因素的影響.數學或者看成是一種人類學現象[26].

上述介紹的歐美數學人類學家研究成果，他們采用的研究方法都類同于如人類學、社會學、民族學、美學、考古學等學科，主要是田野調查，需要進行搜集、整理，觀察、發掘散落于民間的數學文化.在引介的成果中，由于條件限制，沒有翻譯得到更多的相關研究資料，特別是他們最新的研究成果，在此僅作力所能及的介紹.但從中至少能了解到歐美國家對數學人類學的研究輪廓，包括怎么研究、研究什么、誰在研究、什么時候開始研究等，它是一個國際關注的課題.

通過對數學人類學的了解，當前中國學者開展的對某個民族數學文化如蒙古族、苗族、傣族、侗族等進行研究，應該屬于上述介紹的數學人類學研究范疇.對“民族數學”的說法，國內存在分歧，特別是“數學有沒有民族性”問題，這需要進一步的探討，在此研究者不敢妄加評論.但是，關于少數民族聚居區的數學文化類歸為數學人類學，研究者認為無可非議.對于上述的研究雖然在概念上存在分歧，但在中國必定形成雛形.在中國，數學人類學是一個新的研究動向.因此，中國數學人類學研究要立足于中國本土，借助人類學、民族學的研究方法構建真正適合中國本土的數學人類學研究理論框架，形成中國化的一套研究理論和方法.

3 從“民族數學”走向“數學人類學”的研究實踐

凱里學院開展數學人類學研究，經歷了兩個階段：第一階段是所謂“民族數學”研究.從2003年秋開始.當時，羅永超教授認為，要搞好“跨文化數學教育”就應該有豐富的各個民族的數學文化素材，從而思考“侗族數學文化”問題.2006年6月，研究團隊申報凱里學院規劃課題“侗族數學文化與數學教育”獲得立項，并于次年在《數學通報》上發表了《鼓樓人類文明“童年時期”數學文化的結晶》[4]的論文，正式拉開了凱里學院“民族數學”研究的序幕.接著，肖紹菊教授著手于苗族服飾中的數學文化研究.2007年秋，研究者加入了苗侗數學文化研究隊伍，開始思考“民族數學”研究的理論問題.2008年6月，凱里學院成立“民族數學研究所”.第二階段是“數學人類學”研究.2010年，凱里學院副院長、具有跨學科研究視野的徐曉光教授建議思考“數學人類學”的研究問題.研究團隊認為，數學受“社會因素的影響”、“基于生活形式上的約定”[26]，因此，具有歷史性、社會性、地域性，當前研究取得的成果——諸如蒙古族、苗族、羌族、侗族、黎族等的數學文化——僅僅是這些民族聚居在某個固定區域，經過長期的生產和生活發現、形成的數學文化現象.研究者經過近兩年的資料查詢和翻譯，發現歐美國家的學者在20世紀60年代就已經對數學人類學進行了相關探討，并明確提出了“數學人類學”的概念.歐美國家的學者采用的研究方法、分析問題的思路與凱里學院研究團隊（以及國內其他學者）近年來的研究不謀而合.以上現象說明兩個方面問題，一方面是各國、各地區間存在語言各異、文化阻隔的障礙，另一方面是不同國家、不同地域的學者對自然現象和人文科學的研究都會產生相同或相近的方法和路徑.因此，凱里學院研究團隊明確了“數學人類學”這一永久的研究方向.通過近些年的研究，研究者在思考一個問題：一方面，人類學研究在中國已經走過了近一個世紀的歷程，經歷了大起大落之后，中國人類學在面向21世紀之時、在新的起點上正逐漸走向規范化、體系化及本土化，而在中國卻沒有學者關注人類學中的數學分支，包括數字習俗、親屬關系的數理結構、象似符號、隨機現象、數學哲理、數學思想方法及推理現象等；另一方面，中國數學史家一直都致力于中國（包括外國）數學史研究，但是主要是主流文化的數學史料研究，尤其是有記載的皇室數學[27]史料，及文獻的整理和再發掘.那么那些民族民間的“民俗數學”[28]、“被壓制的數學”、“被遺忘的數學”、“本土數學”以及“日常數學”[29]由誰來搜集與研究呢？這就出現了人類學與數學“相聯領域”（sister fields）或“過渡領域”（excesses fields）的研究空白.研究者認為，這些“空白”應該就是歐美國家學者所謂的“數學人類學”，是人類學和數學的“交集”，在中國是一個新的研究動向，是中國數學史家和人類學家共同關注的一個方向.

通過上述分析和比較研究，可以這樣給“數學人類學”進行描述：數學人類學是認知人類學的一個分支，是人類在不同的社會生活環境中，由于語言和習俗各異、思維習慣和解決問題的方式不同，不同地域的文化阻障，不同群體、群落（包括民族、地域差異）經過長期的勞動發現和運用，最終形成的具有差異性的數學文化以及思想方法，包括人類學的數學分支（數字習俗、親屬關系的數理結構、象似符號、隨機現象等）和民族民間數學史料（民俗數學、被壓制的數學、被遺忘的數學、日常數學等），能夠解決當地群落的現實問題，它們散落在民族民間的物質文化和非物質文化包括建筑、服飾、生活用品、宗教習俗、節日祭祀、婚俗禮節、民間習慣法以及生活中的方方面面中.該研究必將豐富地方科技史素材，對地方的物質文明和精神文明建設具有重要的實踐意義，對全國科技史的發展也有不可或缺的學術貢獻.

巴西數學史家達布羅西歐認為，一個新的學術領域的發展一定要有研究團隊、學術研究機構、學術期刊、研討班和定期開展學術研討會等.據此，凱里學院數學人類學研究團隊以《凱里學院學報》為陣營期刊.2012年11月，經過徐曉光主編和傅安輝常務副主編精心策劃，以及《凱里學院學報》學術委員會研究，決定《凱里學院學報》從2012年第6期開始開辟了“數學人類學”欄目.并且在這一期，該欄目首次推出3篇數學人類學文章.徐曉光的《原生態民族法文化中的數字與象征符號》，從法律人類學視角探討了中國歷史上各少數民族在不斷地認識事物，以及相互社會交往中形成的以數字、刻木、草符為載體的法文化符號體系.張和平的《民族數學與數學人類學研究述略》，介紹了中外學者“民族數學文化”研究概況，引介歐美專家關于“數學人類學”研究取得的理論成果，并且對當前中國學者研究現象存在的盲點進行分析.羅永超等的《侗族數學文化與數學教育》，調查侗族生活中使用的數學知識以及鼓樓建筑中蘊含的數學文化，思考民族地區數學文化教育的路徑.該欄目的開設，旨在給全國的數學人類學研究提供學術交流平臺，吸納學術隊伍，讓更多的學者參與思考、研究數學人類學這一國際性的課題.

[1]劉志軍.國際人類學與民族學聯合會簡介[J].廣西民族學院學報，2005，（1）：59-61.

[2]代欽.蒙古族傳統生活中的數學文化[J].內蒙古師大學報，1996，（2）：42-47.

[3]周開瑞，王世芳.羌族數學探源[J].西南民族學院學報，2000，（4）：427-433.

[4]羅永超.鼓樓人類文明“童年時期”數學文化的結晶[J].數學通報，2007，（11）：9-11.

[5]羅永超.侗族數學文化中的2與1/2及相關計算[J].凱里學院學報，2008，（3）：13-15.

[6]肖紹菊.苗族服飾的數學因素挖掘及其數學美[J].貴州民族研究，2008，（6）：106-112.

[7]張和平，羅永超，肖紹菊.研究性學習與原生態民族文化資源開發實踐研究——以黔東南苗族服飾和侗族鼓樓蘊涵數學文化為例[J].數學教育學報，2009，18（6）：70-73.

[8]張和平，唐興蕓.苗族文化中的數學智慧——兼談與古典數學的共通性比較[J].貴州民族研究，2012，（1）：62-68.

[9]張和平.苗族民俗數學及其與《周易》的比較[J].數學教育學報，2011，20（4）：75-79.

[10]周長軍，申玉紅，楊啟祥.云南德宏傣族文化中的數學因素調查分析[J].數學教育學報，2010，19（3）：56-59.

[11]周長軍，申玉紅，楊啟祥.德宏傣族日常生活中的幾何因素探析[J].貴州民族研究，2010，（6）：76-79.

[12]王奮平，陳穎樹.聚焦黎族數學文化[J].數學教育學報，2010，19（4）：70-72.

[13]劉超，張茜，拉扎提·納斯哈提.新疆哈薩克族數學文化調查分析[J].兵團教育學院學報，2012，（4）：17-25.

[14]維特根斯坦.維特根斯坦劍橋講演錄[M].周曉亮，江怡譯.杭州：浙江大學出版社，2010.

[15]張維忠，唐恒鈞.民族數學與數學課程改革[J].數學傳播，2008，（4）：80-90.

[16]張和平.民族數學與數學人類學研究述略[J].凱里學院學報，2012，（6）：7-10.

[17]申玉紅，楊啟祥，周長軍.少數民族數學文化研究成果綜述[J].數學教育學報，2012，21（2）：17-19.

[18]呂傳漢，張洪林.民族數學文化與數學教育[J].數學教育學報，1992，1（1）：101-104.

[19]劉超，張茜，陸書環.基于民族數學的少數民族數學教育探析[J].數學教育學報，2012，21（5）：49-52.

[20]保羅·W·迪克森.文化與會意：數學才能和表現與神經生理的關聯性[A].朱葉娜譯.皮特·J·M·納斯，張繼焦.當今國際人類學——國際人類與民族學聯合會的歷史及其各專業委員會的論文[C].北京：知識產權出版社，2009.

[21]Alan J Bishop.Mathematical Enculturation: A Cultural Perspective on Mathematical Education [M].Kluwer Academic Publishers, 1988.

[22]Hoffman H.Mathematical Anthropology [J].Bien.Rev.Anthropo, 1969, (6): 41-79.

[23]Burton, Michael L.Mathematical Anthropology [J].Annual Review of Anthropology, 1973, (2): 189-199.

[24]White D R.Mathematical Anthropology [A].Honigmann J J.Handbook of Social and Cultural Anthropology [C].Chicago: Rand McNally, 1972.

[25]托馬斯·克倫普.數字人類學[M].鄭元者譯.北京：中央編譯出版社，2007.

[26]樊岳紅，魏屹東.數學：一種人類學現象——后期維特根斯坦數學哲學思想探析[J].自然辯證法通訊，2012，（5）：53-58.

[27]張奠宙，梁紹君，金家梁.數學文化的一些新視角[J].數學教育學報，2003，12（1）：39-40.

[28]章勤瓊，張維忠.民族數學及其對數學課程改革的啟示[J].數學教育學報，2008，17（4）：15-17.

[29]鄭毓信.民俗數學與數學教育[J].貴州師范大學學報，1999，（4）：90-95.