磁懸浮列車懸浮高度控制技術的研究

李 森

（上海出版印刷高等專科學校，上海 200093）

0 引言

懸浮控制技術是磁浮列車的核心和關鍵技術之一，懸浮控制系統(tǒng)性能的好壞將直接影響到磁浮列車的穩(wěn)定性、安全性和舒適性。磁懸浮列車控制的一個最基本要求是要保證磁浮列車能夠在一定程度的各種擾動作用下具有平衡穩(wěn)定的懸浮。作用在磁懸浮系統(tǒng)的外部擾動主要包括負載變化、驅動加速力和減速力、空氣動力及軌道的彎度、坡道和不平整帶來的擾動力;內(nèi)部擾動力則主要起因于控制系統(tǒng)本身的非線性和傳感器的測量誤差等因素。磁浮列車在控制系統(tǒng)設計時應考慮和解決這些因素。

本文運用計算機控制系統(tǒng)來解決這一問題，它的優(yōu)點是:

(1)運算速度快、精度高、具有極豐富的邏輯判斷功能和大容量的存儲能力，容易實現(xiàn)復雜的控制規(guī)律，極大地提高系統(tǒng)性能。

(2)功能/價格比高。

(3)控制算法由軟件程序實現(xiàn)，適應性強、靈活性高。

(4)可使用各種數(shù)字部件，從而提高系統(tǒng)測量靈敏度，并可利用數(shù)字通信來傳輸信息。

(5)使控制與管理更易結合，并實現(xiàn)更高層次的自動化。

(6)實現(xiàn)自動檢測和故障診斷較為方便，故提高了系統(tǒng)的可靠性和容錯及維修能力。

1 實例介紹

自動化的磁懸浮列車可以在極短的時間內(nèi)正常運行，而且具有極高的速度和能量利用率。自動化磁懸浮列車的一個關鍵技術就是對列車的懸浮高度進行控制。德國M-Bahn號磁懸浮列車懸浮高度的計算機控制系統(tǒng)代表世界先進水平。

1.1 建立高度控制的數(shù)學模型

若采樣周期 T=0.01 s，試在w'域設計數(shù)字控制器D(z)，使系統(tǒng)的相位裕度滿足45°≤γ≤55°，并估算校正后的系統(tǒng)階躍響應。

1.2 實例驗證數(shù)學模型

把被控對象離散化可得:

采用MATLAB命令:

得到運行結果為:

要想判斷系統(tǒng)是否處于穩(wěn)定狀態(tài)，需要判斷系統(tǒng)特征方程的特征根，根據(jù)特征根與單位圓的關系，可以粗略判斷系統(tǒng)的穩(wěn)定性。

特征方程根為:

分析:因為有根是在單位圓以外，所以原系統(tǒng)不是穩(wěn)定的。

將其變換至 w'平面，若，T=0.01 s，則可以采用MATLAB軟件中突斯丁反變換指令，將其由Z平面變換至w'平面:

運行結果為:

采用MATLAB命令:

figure(1);margin(Gnum，Gdes)，grid ，hold on%連續(xù)系統(tǒng)在S平面。

margin(Gwnum，Gwdes)%原連續(xù)系統(tǒng)在W平面可以得到該模型的輸出伯德圖如圖1所示，所設計的校正系統(tǒng)如圖2所示，校正后的系統(tǒng)階躍響應如圖3所示。

畫出對象模型的幾種頻率特性曲線如圖4所示。

從圖4中可以看出，在頻率小于50 rad/s時，3種曲線對應的相角幾乎相等，不需要進行相角的修正。

2 Mathmatica中的仿真

前面采用傳遞函數(shù)的方法進行仿真和分析，通過matlab等軟件對磁懸浮列車的高度控制進行仿真，下面用狀態(tài)空間的方法對磁懸浮列車的高度控制進行分析。

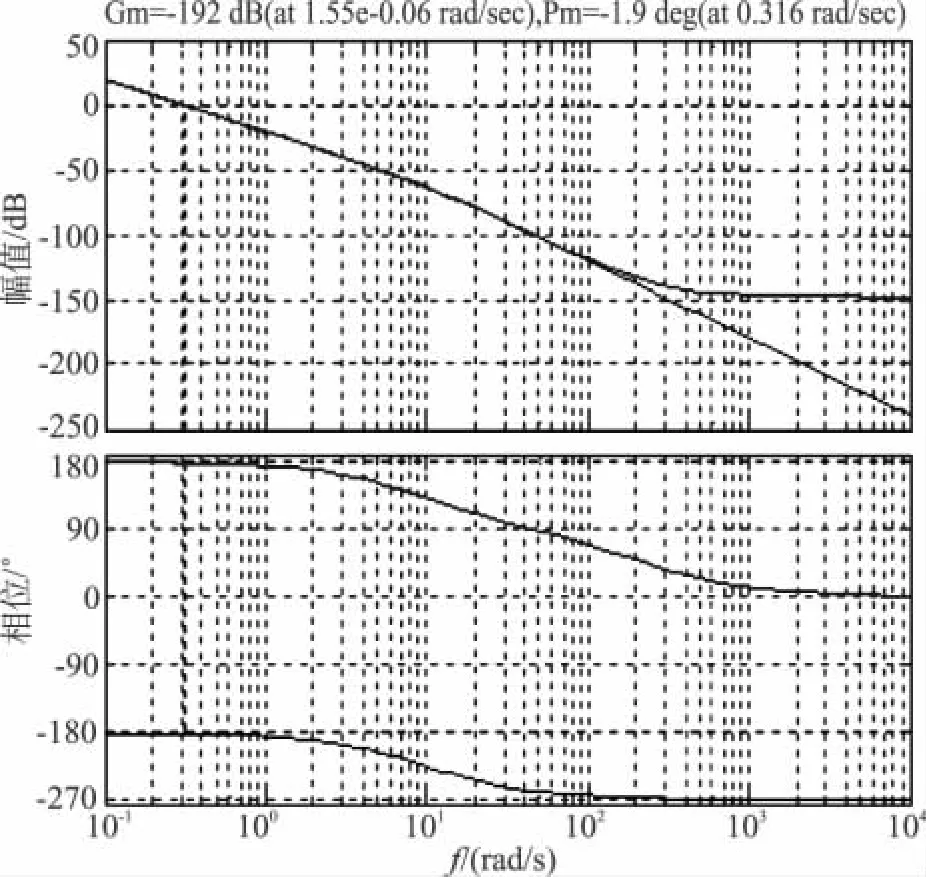
圖1 仿真伯德圖

圖2 matlab控制系統(tǒng)結構圖

圖3 matlab階躍響應仿真結果

首先，傳遞函數(shù)轉化為狀態(tài)空間形式，然后把狀態(tài)變量離散化。

原傳遞函數(shù)的空間狀態(tài)矩陣為:

運用matlab把連續(xù)的狀態(tài)矩陣轉換為離散的狀態(tài)矩陣:

圖4 仿真結果圖

運用mathmatica判斷系統(tǒng)的可控性和可觀性，如圖5所示。

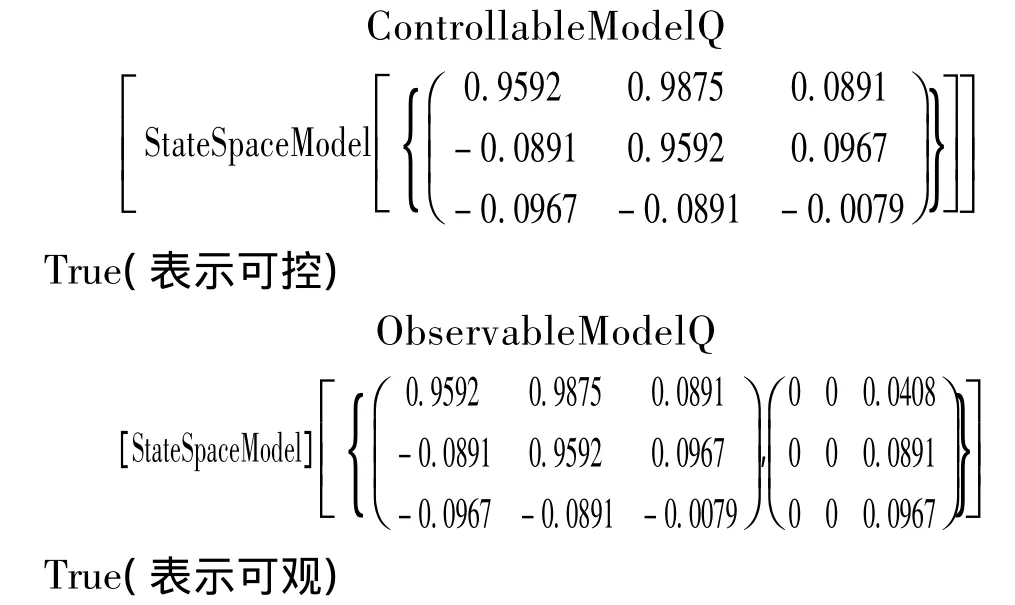
圖5 mathmatica控制系統(tǒng)結構

計算系統(tǒng)的增益矩陣:

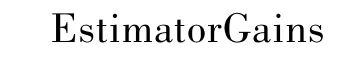
得到的增益矩陣:

3 實驗總結

微機控制系統(tǒng)設計雖然隨控制對象、設備種類、控制方式、規(guī)模大小等不同而有所差異，但系統(tǒng)設計的基本內(nèi)容和主要步驟是大體相同的。主要包括:

(1)系統(tǒng)總體控制方案設計;

(2)系統(tǒng)硬件設計、選擇與開發(fā);

(3)軟硬件的可靠性設計;

(4)確定滿足一定經(jīng)濟指標的目標函數(shù)，建立被控對象的數(shù)學模型并針對目標函數(shù)進行控制算法規(guī)律設計;

(5)軟件設計與開發(fā);

(6)系統(tǒng)整體調(diào)試等。

通過MATLAB軟件，容易檢驗輸出的穩(wěn)定性，得到實驗結果，通過圖像可以看出輸出曲線的超調(diào)量、穩(wěn)定時間、調(diào)節(jié)時間等，從而進行分析。

(1)采用兩個微分環(huán)節(jié)抵消積分環(huán)節(jié)，所以系統(tǒng)響應存在靜態(tài)誤差。

(2)設計中沒有考慮w'平面與s平面在頻率和相角之間存在的非線性映射關系，得到的相角裕度是在w'平面的，而不是在z平面的，所以可能需要進行一定的修正。

(3)采用1個微分環(huán)節(jié)抵消積分環(huán)節(jié)，所以系統(tǒng)響應不存在靜態(tài)誤差。

(4)穿越頻率 5.69 rad/s比較小，相角裕度為47°，所以得到的相角裕度不需要進行修正。

控制系統(tǒng)動力穩(wěn)定性分析方面，主要根據(jù)系統(tǒng)動力特性的數(shù)值研究、數(shù)值仿真結果，得出系統(tǒng)受控穩(wěn)定情況下的控制參數(shù)。現(xiàn)實中要考慮各個非理想的因素，設計的控制器以及各變量會影響實際運行結果，而本設計只在實驗室中進行仿真，只考慮最主要的幾個因素進行控制，設計的控制器比較理想。

［1］BrezezinaW ，Langerhols J.Lift and side forces on rectangular pole pieces in two dimensions［J］.Journal of Applied physics，1974 ，45(4):1868-1872.

［2］謝云德，常文森.電磁型磁浮列車單鐵力的計算及運動穩(wěn)定性和可控性研究［J］.鐵道學報，1995，16(1):41-48

［3］Masada E.Development of Maglev Transportation in Japan:Present State and FU TURE Prospects［ A ］.Maglev＇93［C］.Argonne:Argonne National laboratory，May 1993.

［4］Seki，Tomohiro.The Development of HSST21001.Engineer2 ing Development［C］.Tokyo.Japan:HSST Develoopment Corporation，Chiyoda2ku，1995.

［5］Matsumoto A.Vehicle Dynamics and Riding Quality of a Maglev2Type Urban Transportaion System CHSST2100［C］.The International Conference on Speed Up Rechnology for Tailway and Maglev Vehicels.Yokohama:J SME ，Nov.1993.

［6］尹力明.磁懸浮轉向架的動力學關系及部件強度的計算方法［J］.機車電傳動，1997，(5):7-10.

［7］Yoshioka H.山梨磁懸浮試驗線車輛ML X01的動力學性能［J］.國外鐵道車輛，2000 ，37(5):27-32

［8］Yoshioka H ，Watanabe K.Dynamic characteristics of side2 wall magnetically2levitated vehicles［C］.Proceedings of the international Conference on Speedup Technology for Railway and Maglev Vehicles.1993:103-108.

［9］Yoshioka H，Suzuki E，Seino HE，Azakami M ，Oshima H ，Nakanishi T.Results of running tests and characteristics of the dynamics of the ML X01 Yamanashi Maglev Test Line ve2 hicles［C］.Proceedings of the 15th international Conferences on MA GL EV'98.1998:25-230.

［10］Hiroshi Yoshioka，Erimitsu Suzuki，Hiroshi Seino et al.Characteristics of the Dynamics of the ML X01 Yamanashi Maglev Test Line Vehicles［J］.Quarterly Report of RTRI ，1998，39(2):35-38.

［11］趙志蘇，尹力明，羅 昆.磁懸浮列車轉向機構運動分析與設計［J］.機車電傳動，2000，(6):11-13.