帶極點約束離散廣義分段仿射系統的H∞保性能控制

王茂，周振華，王學翰

(1.哈爾濱工業大學空間控制與慣性技術研究中心，黑龍江 哈爾濱150000;2.大慶油田電力集團燃機電廠，黑龍江 大慶230604)

目前，具有范數有界時變參數不確定性廣義分段仿射系統的魯棒穩定性問題越來越受到人們的關注［1-3］，但關于二次D-穩定性的研究確少有報道。為使這樣的系統不但具有魯棒穩定性，同時也需要滿足某些性能指標［4］，二次型性能指標提出的主要思想是對具有參數不確定性的系統設計一個控制律，不僅使得閉環系統漸進穩定，而且使得閉環系統的性能不超過某個給定的性能上界［5-7］。

隨著廣義分段仿射系統魯棒控制問題研究的深入，對其進行保性能控制的研究也相繼取得了一些成果［8-10］。然而，目前這方面的研究大多局限于連續系統，而所采用的方法主要是基于分段Lyapunov函數法以及一些相應線性矩陣不等式的處理方法［11-13］。王茂等研究了一類具有參數不確定離散廣義分段仿射系統的靜態輸出反饋控制問題［14］，通過求解一組包含參變量的LMIs得到保證廣義分段仿射系統容許的反饋控制器增益。本文基于分段Lyapunov函數，投影定理以及幾個基本引理，在前人的基礎上引入帶極點約束H∞保性能控制方法對離散廣義分段仿射系統設計一個魯棒H∞靜態輸出反饋保性能控制器。

文章的研究對象是一類具有時變參數不確定性的離散廣義分段仿射系統，且不確定性體現為范數有界，本文特點在于將二次D-穩定性與H∞性能指標同時進行考慮，使得由控制器構成的閉環系統具有二次D-穩定性，且同時滿足魯棒H∞性能指標以及預先給定的二次型性能指標。

1 系統描述及預備知識

本文的研究對象是一類參數不確定性體現為范數有界形式的離散時間廣義分段仿射系統:

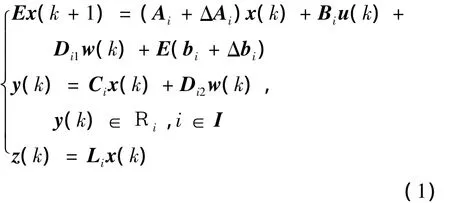
式中:x(k)∈Rnx為系統狀態變量;u(k)∈Rnu為控制輸入向量;y(k)∈Rny為系統輸出向量;z(k)∈Rnz為可控輸出向量;w(k)∈Rnw，w(k)∈l2［0，∞)為擾動輸入;Ri代表第i個子系統多面體區域，Ai、Bi、Ci、Di1、Di2、Li、bi、E為第i個子系統的已知定常系數矩陣;Ebi是偏置項;索引集合是I={1，2，…，N};E∈是廣義矩陣，且rank(E)=r≤nx;ΔAi和Δbi代表系統的不確定項，且滿足如下形式:

式中:Wi1、Ei1和Ei2是已知的實定常矩陣，且具有適當維數，Δi(t):Z+→Rs1×s2是一個未知實值矩陣函數，且該時變矩陣函數包含Lebesgue可測量元素，具有如下形式;

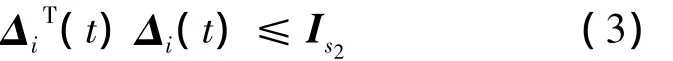
如果式(2)和式(3)成立，則稱系統具有容許的參數不確定性。

將系統從多面體區域Ri過渡到Rj的集合用Ω表示，可以描述為

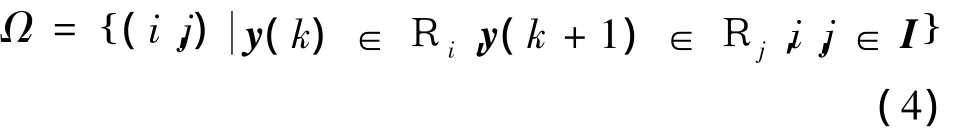
本文假設多面體區域Ri，i∈I具有形式:

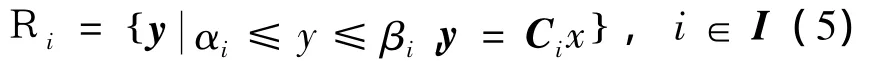
該多面體區域可進一步描述為一個橢圓集合，其中

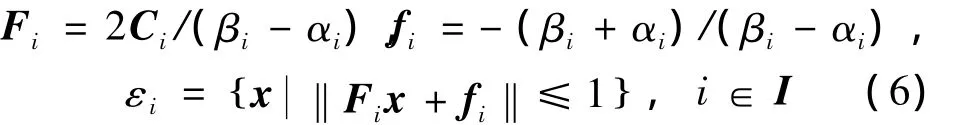
對于每個橢圓區域，可以得到

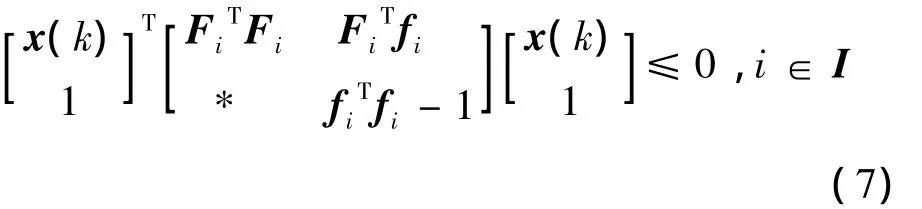
進一步將狀態空間分為兩類區域I=I0∪I1，I0代表包含原點的-1≤0索引集合區域，則其余的索引集合區域用I1表示。

定義1［15］考慮參數不確定廣義分段仿射系統式(1)，其中u(k)=0;

1)如果存在z∈C使得det(zE-Ai)≠0，則稱廣義系統(1)是正則的，i∈I;

2)如果 deg(det(zE-Ai))=rank(E)，i∈ I則稱廣義系統(1)是因果的;

3)如果離散廣義系統(1)的所有特征根λ(E，Ai)?Dint(0，1)，則稱系統(1)穩定;

4)如果系統(1)是正則、因果，并且穩定的，則稱廣義系統(1)是容許的;

5)任意非零向量ν1，若滿足Eν1=0，則稱其為矩陣束 (E，Ai)的一階向量，對于滿足 Eνk=Aiνk-1的非零特征向量νk(k≥2)，則稱為矩陣束(E，Ai)的k階特征向量。

以下定義2和定義3，所考慮廣義系統一般形式為

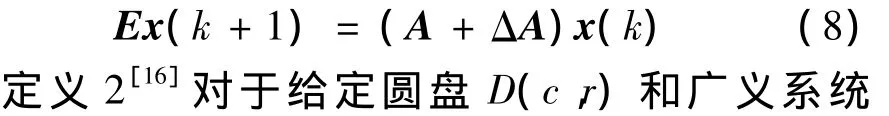
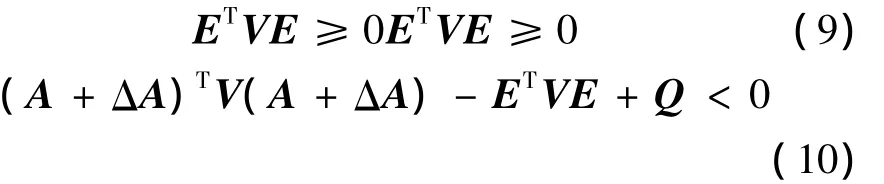
則稱V為廣義系統(8)的一個二次性能矩陣，相應的閉環性能指標值J≤Vx0。x0為系統初始狀態。

定義3［16］對于給定圓盤 D(c，r)，廣義系統式(8)若存在對稱可逆矩陣T，對所有的ΔA，對稱可逆矩陣T滿足式(9)以及:

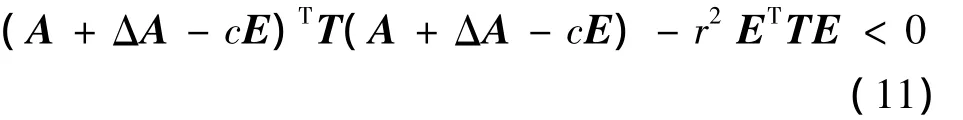
則稱廣義系統式(8)是二次D-穩定的。若對稱可逆矩陣T同時滿足式(9)和式(11)，則稱對稱可逆矩陣T為廣義系統式(8)的一個二次D-性能矩陣。

引理1 對于適當維數實矩陣M=MT、S、N和Θ(t)，若滿足ΘT(t)Θ(t)≤I，則當且僅當存在某個標量ε＞0，使M+SΘ(t)N+NTΘT(t)ST＜0等價于M+εSST+ε-1NTN ＜0。

應用shcur補引理，M+εSST+ε-1NTN ＜0可以進一步表述為以下2種形式:

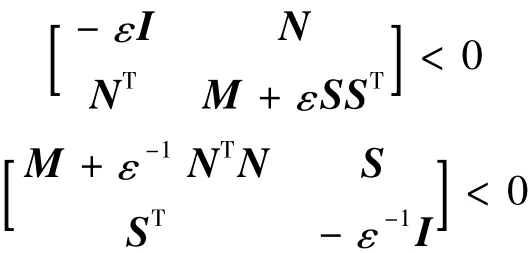
引理2［17］(投影定理) 給定矩陣h=hT∈Rn×n，u∈Rk×n和v∈Rm×n，則關于變量Φ的矩陣不等式h+uTΦTv+vTΦu＜0是LMI可解的，當且僅當:

1)若 v⊥=0，u⊥≠ 0，則 uT⊥hu⊥＜ 0

2)若 u⊥=0，v⊥≠ 0，則 vT⊥hv⊥＜ 0

3)若 u⊥≠0，v⊥≠0，則 uT⊥hu⊥＜ 0，vT⊥hv⊥＜0同時成立，u⊥，v⊥代表u和v的右正交核空間。

本文針對具有參數不確定性離散時間廣義分段仿射系統式(1)設計H∞輸出反饋保性能控制器:

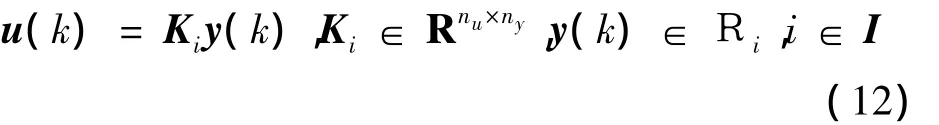
保證閉環系統:

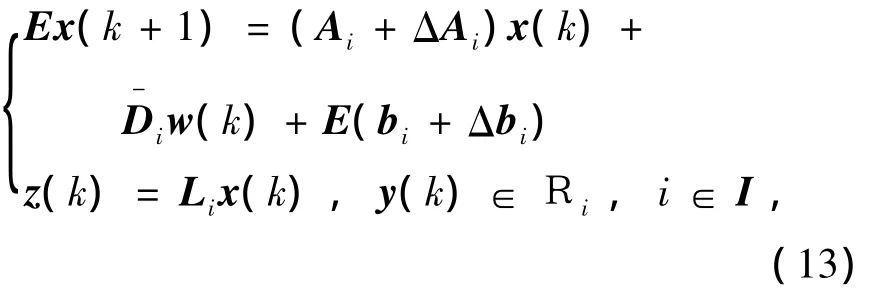
式中系統狀態矩陣:Ai=Ai+BiKiCi，擾動矩陣:=Di1+BiKiDi2)是容許的，且具有二次D-穩定性，滿足性能指標:

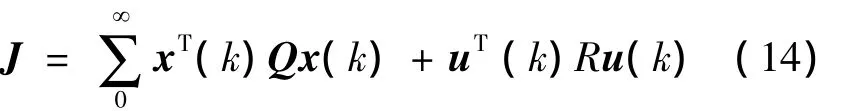
式中:Q、R為已知正定加權矩陣。

2 主要結果

假設系統式(1)的輸入矩陣Bi，i∈I是列滿秩的，則存在一組轉換矩陣 TBi∈ Rnx×nx，i∈ I ，滿足:

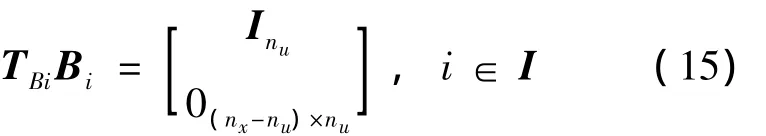
且轉換矩陣 TBi∈Rnx×nx非奇異，以下 H∞靜態輸出反饋保性能控制器就是基于該假設進行設計的。

定理1 考慮參數不確定離散廣義分段仿射系統(1)，若存在對稱矩陣 Pi∈ Rnx×nx，標量:

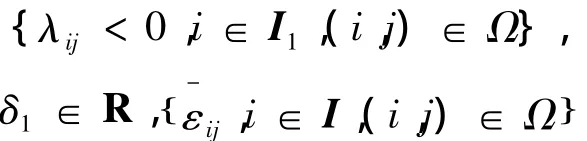
以及:

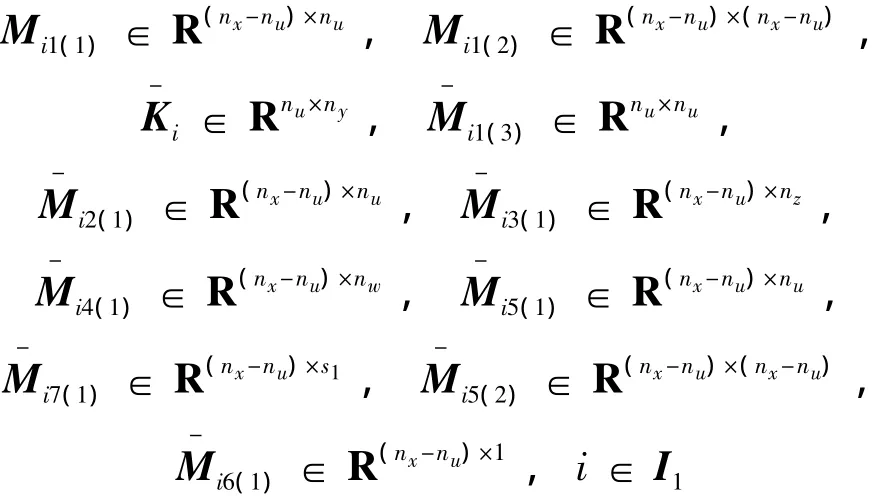
使得

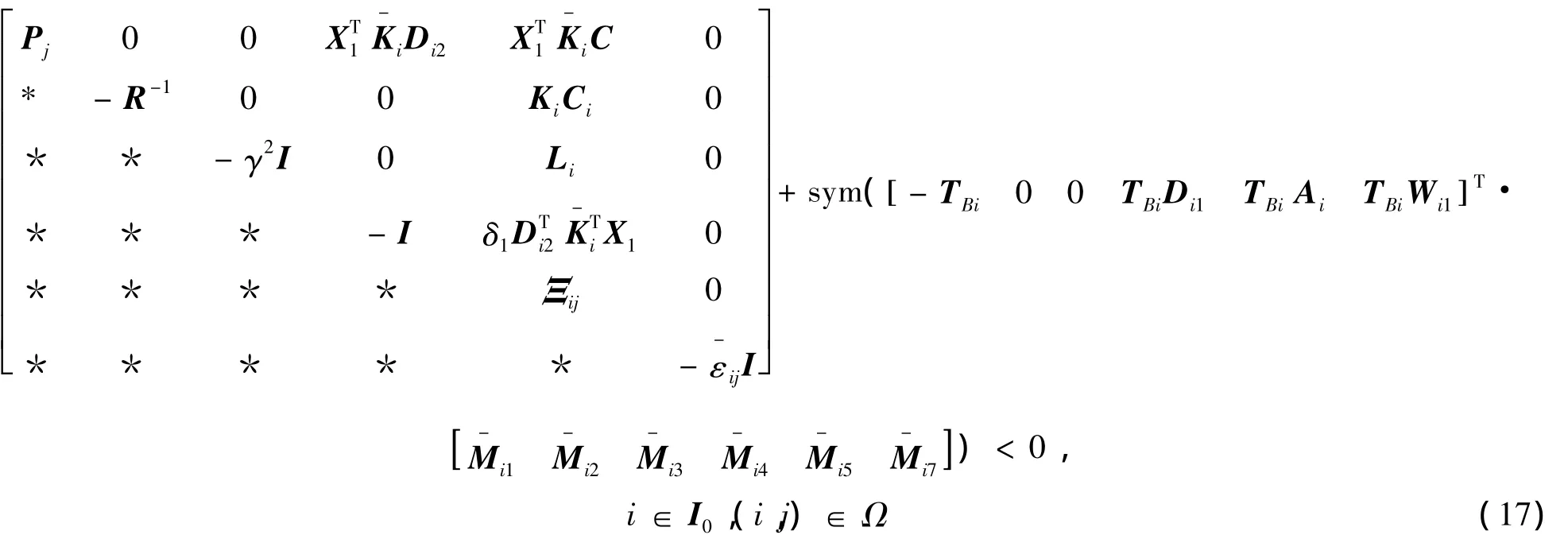
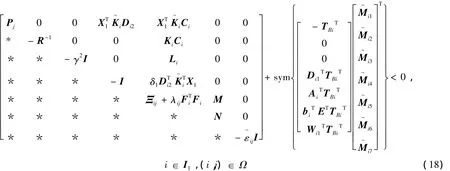
成立，則存在H∞輸出反饋保性能控制器式(12)，使得閉環系統式(13)是容許的，且滿足二次性能指標式(14)，即Pi∈Rnx×nx為閉環系統式(13)的一個二次性能矩陣。

對任意矩陣H，sym{H}=H+HT。

H∞輸出反饋保性能控制器增益:

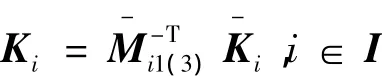
證明:可以看到條件式(18)在Ebi=0時，就是條件式(17)。不失一般性，如下可以只證明條件式(18)成立。

選取廣義分段仿射Lyapunov函數:

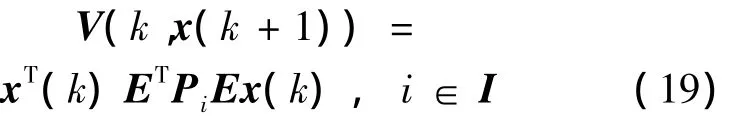
進一步:

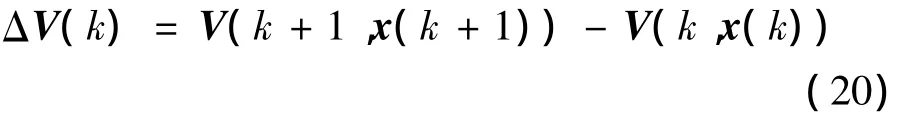
基于Lyapunov函數的定義，為使閉環系統式(13)具有魯棒H∞性能指標γ，則只需保證以下不等式成立:

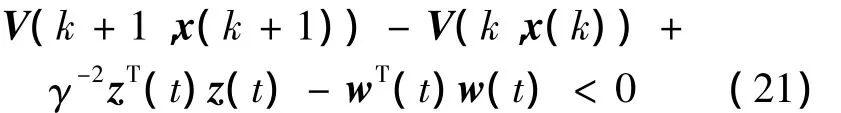
對于閉環系統式(13)，根據定義2關于二次性能矩陣的定義，如果下面不等式成立，則系統具有H∞二次保性能矩陣Pi:

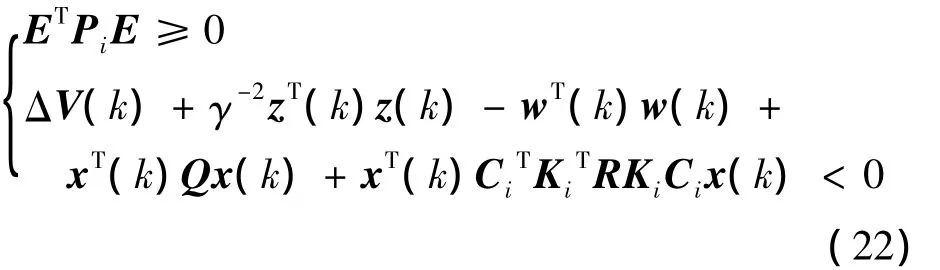
對于任意非零w(k)∈l2［0，∞)，式(22)可進一步等價于:

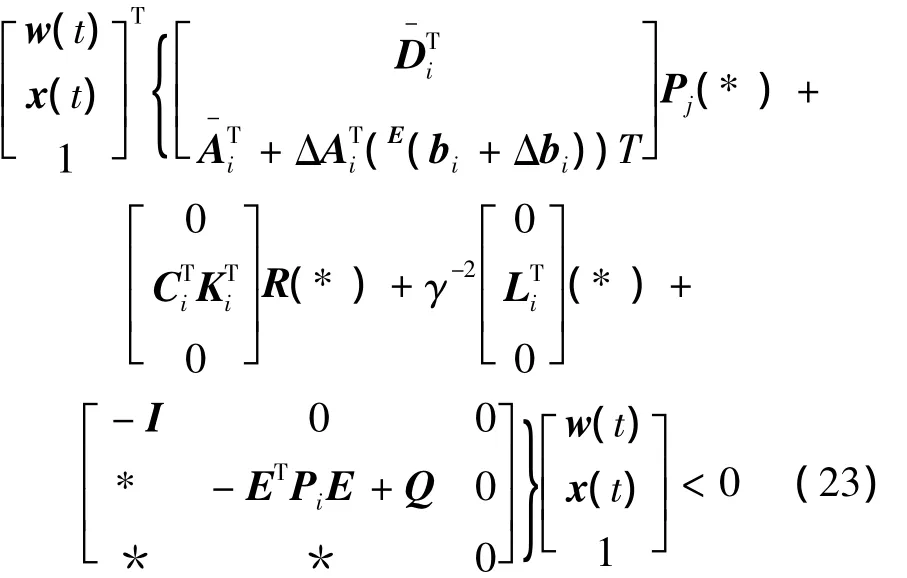
從式(23)可以得到:

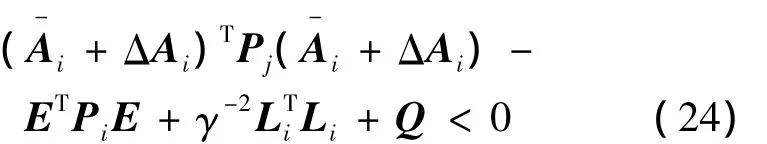
即

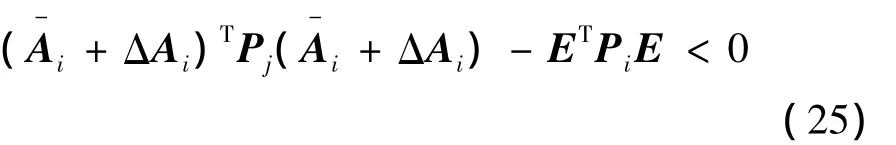
假設矩陣束(E，Ai)是非因果的。用一階特征向量ν1和它的Hermitian矩陣ν1*分別左乘和右乘式(25)得

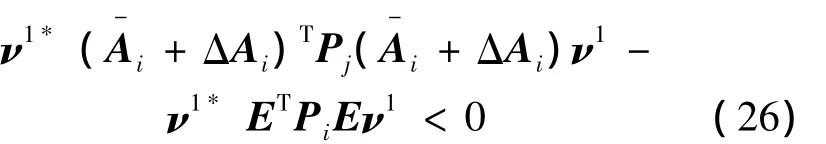
接下來引用schur補引理，再用Eν2代替Aiν1，并注意到Eν1=0，可以得到

與條件式(16)相矛盾。所以得到矩陣束(E，Ai)是因果的。顯然，證明因果性的同時也證明了矩陣束(E，Ai)的正則性。

考慮區域信息，即將式(7)代入式(23)并應用 S-procedure，其中 λij＜ 0，i∈ I1，(i，j)∈ Ω ，得到

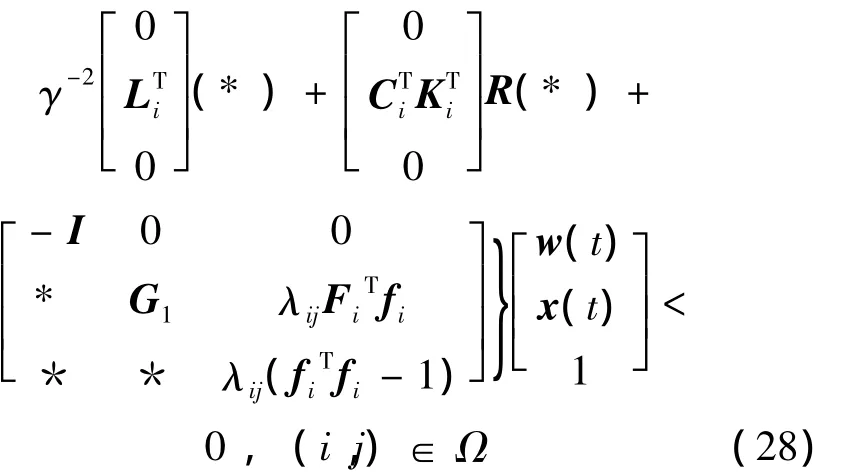
式中:G1=-ETPiE+λijFiTFi+Q。對式(28)中各個矩陣進行合并，并先后應用3次Schur補引理，從式(28)可以得到

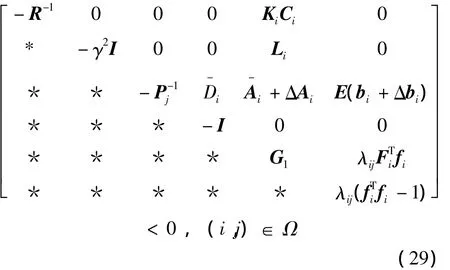
另一方面，為消除不確定性給求解過程帶來的影響，將式(29)中的不確定性ΔAi和EΔbi分離出來，可以將式(29)改寫為

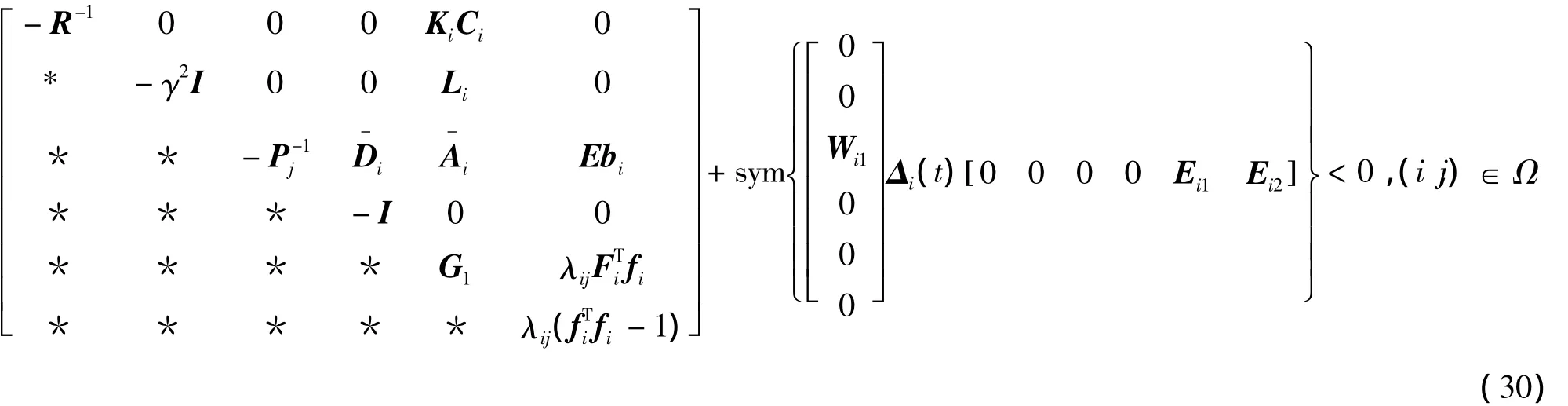
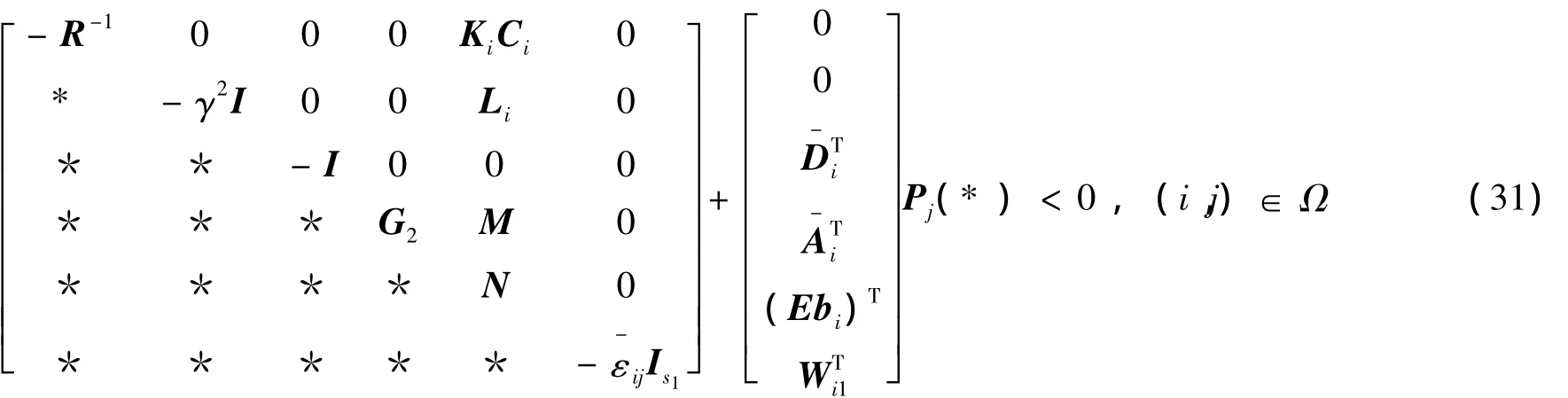
式中，G=-ETP E+λF+E+Q。系

2

iiji1統矩陣與Lyapunov矩陣相耦合。因此以下應用投，(31)影定理消去這種耦合關系 將式 改寫成為

基于投影定理，做如下變量替換:

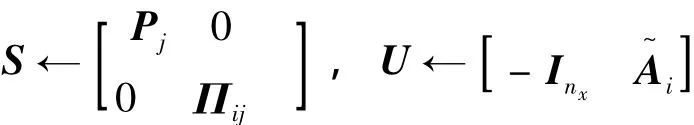
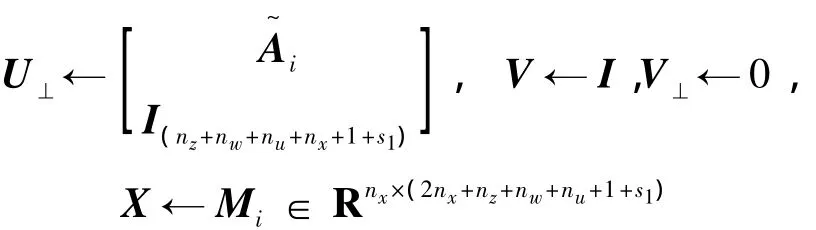
應用引理2的投影定理，得到

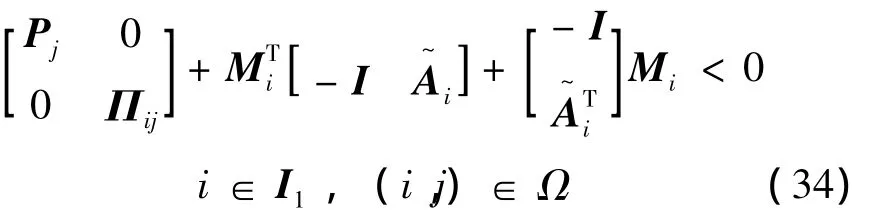
對矩陣 Mi∈ Rnx×(2nx+nz+nw+nu+1+s1)，i∈ I1進行分塊:

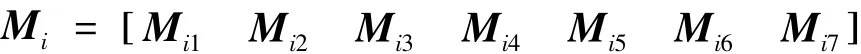
其中:

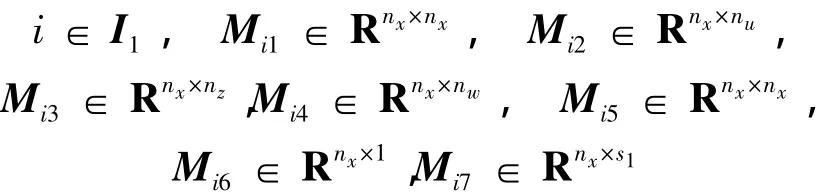
相應矩陣的定義與定理1中給出的形式一樣。結合變量δ1:

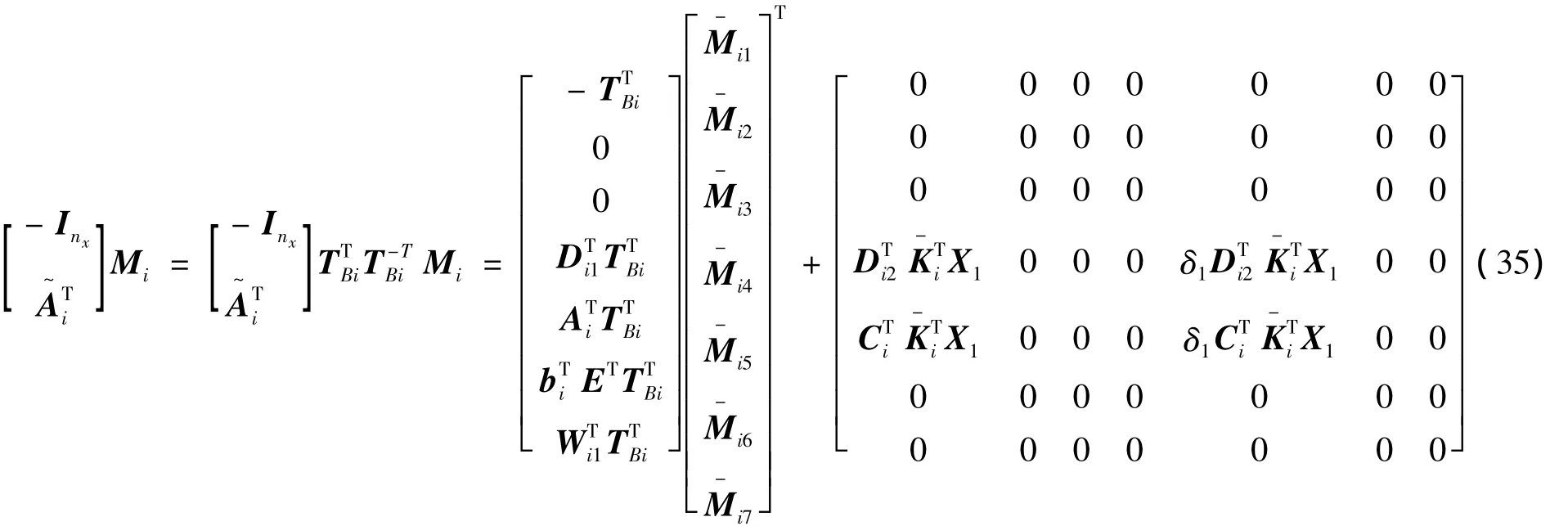
將式(35)代入到式(34)中，并結合所有給定矩陣的定義，最終得到式(18)，第一部分證明結束。

另一方面，從式(17)、(18)可以得到

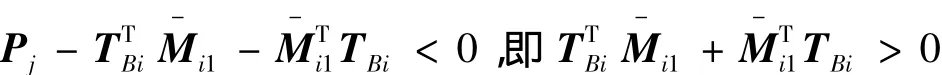
--性，并且由 Mi1是下三角陣，可以得到 Mi1(3)可逆。所以控制器增益能夠得到，定理進一步證明完畢。

定理2 考慮范數有界離散廣義分段仿射系統式(1)，若存在對稱矩陣 Pi∈ Rnx×nx，標量:

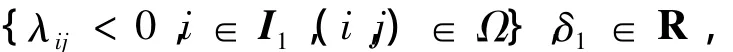
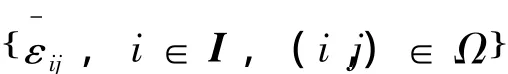
以及

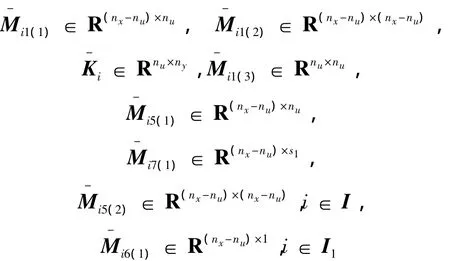
使得式(16)～(18)成立，且滿足以下不等式:

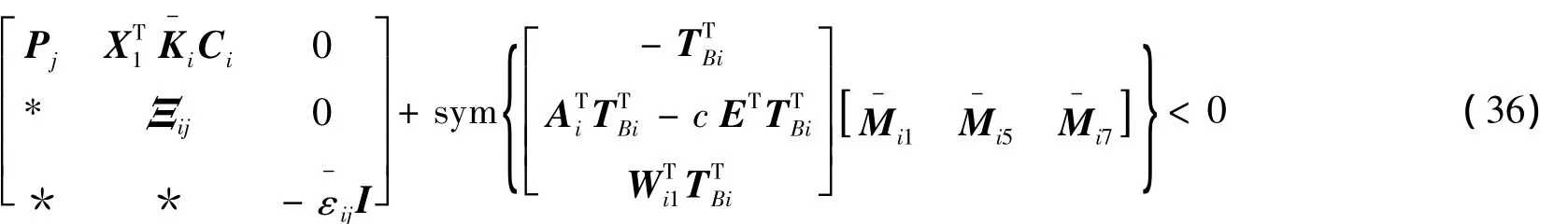
則存在H∞靜態輸出反饋保性能控制器式(12)，使得閉環系統式(13)具有二次D-穩定性，且對于所給二次型性能指標式(14)，Pi為一個二次D-性能矩陣。則閉環系統式(13)的控制器增益:

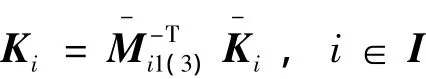
閉環系統式(13)相應的性能上界為

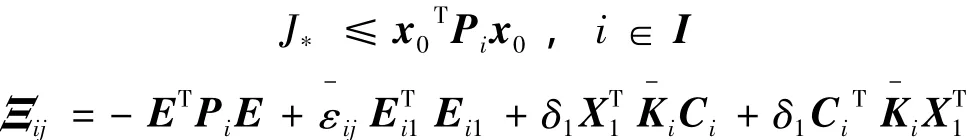
證明 首先，由定義3可知，若一般形式廣義系統式(8)是二次D-穩定的，則存在對稱可逆矩陣Pi必須同時滿足以下2個不等式:

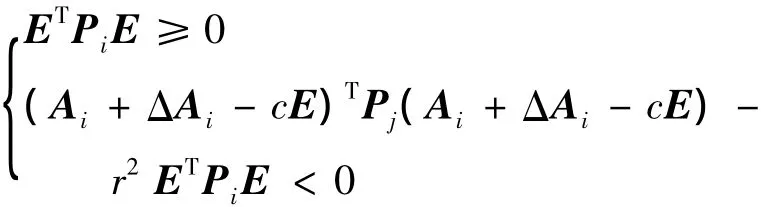
第1個不等式與條件式(16)相同，第2個不等式也等價于:

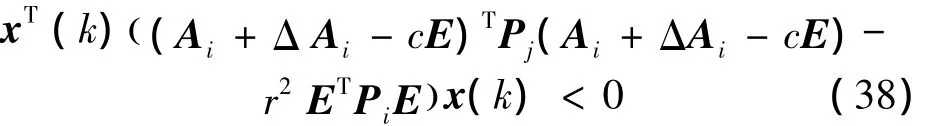
推廣到本文所考慮的離散廣義分段仿射系統式(1)，若使系統式(1)是二次D-穩定的，只需滿足條件式(16)以及以下不等式:

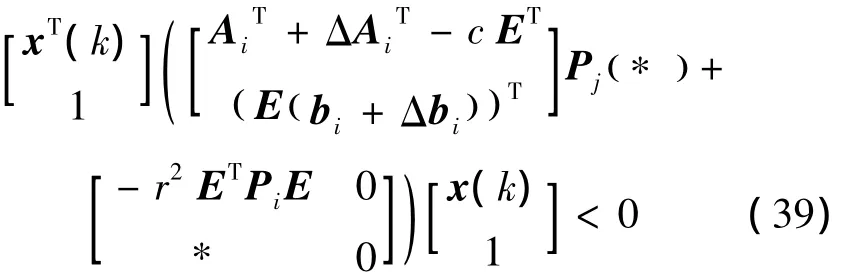
考慮區域信息，將式(7)代入式(39)中，并且應用S-procedure引理，即可得:＞ 0

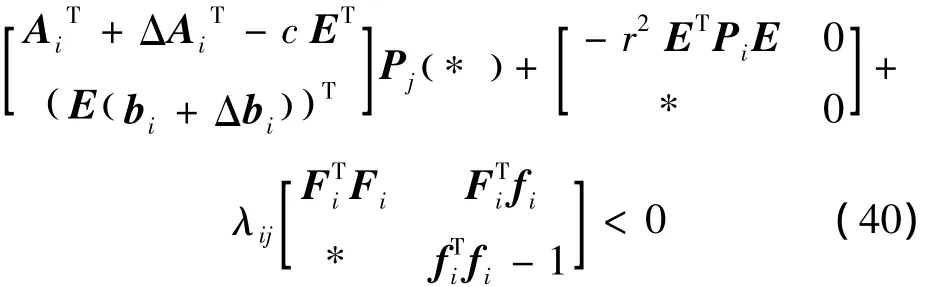
基于定理2，引入一組標量 ，i∈ I1，(i，j)∈Ω，并引用schur補引理，不等式:

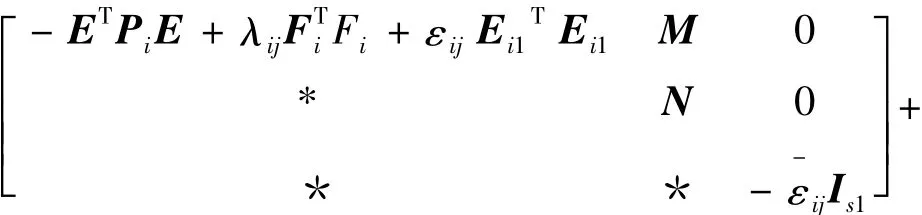
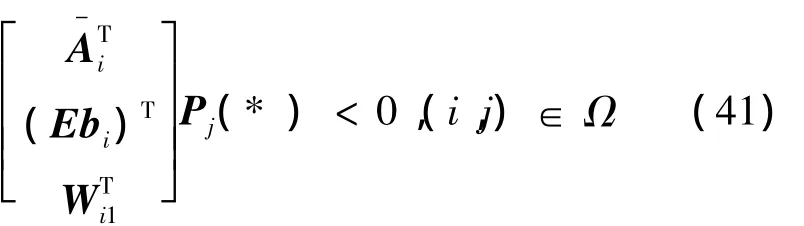
與式(40)等價，其中M和N的定義見定理1。

以下證明方法與定理1相同，去掉系統矩陣和Lyapunov矩陣的耦合關系之后，即可得到條件式(36)、(37)。顯然，根據定理 1，由于 Pi滿足式(16)、(18)，則Pi為閉環系統式(13)的一個二次性能矩陣，而Pi又滿足式(36)、(37)，所以Pi為閉環系統式(13)的一個二次D-性能矩陣，定理2得證。

3 數值仿真

由于本文所考慮離散廣義分段仿射系統存在外部擾動輸入，應用定理1設計得到的控制器，應使得由此構成的閉環系統式(13)具有魯棒H∞性能，且滿足預先給定的二次型性能指標。然而，基于定理2設計控制器的主要思想則是考慮將閉環系統式(13)的極點配置在所期望的位置上，以保證系統具有實際工程中所要求的動態和穩態性能，與此同時，閉環系統式(13)還應滿足一定的H∞性能指標和二次型性能指標。

考慮參數不確定性體現為范數有界形式的離散廣義分段仿射系統式(1)由以下2個子系統組成:

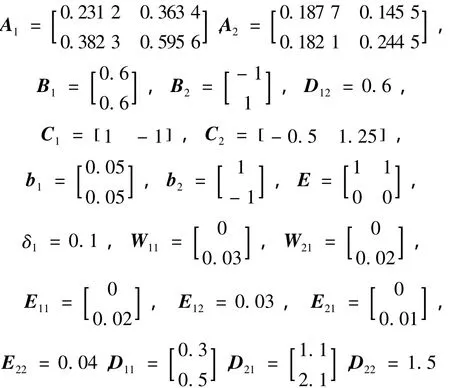
橢圓體系數矩陣:

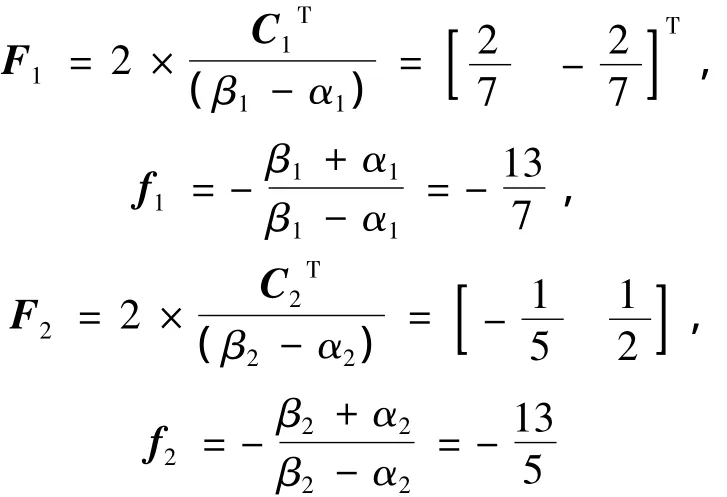
式中:α1=3，β1=10，α2=4，β2=9 ，R=5，Q=。系統初始狀態x0=[1 1]T系統擾動輸入向量w =[2 1]TL1= [0.1 0.2 ]，L2=[0.3 0.4 ]圓盤 D(c，r):c1=-5，c2=-10，r1=5，r2=10應用定理1得到閉環系統式(13)的一個二次性能矩陣以及使閉環系統式(13)容許的H∞靜態輸出反饋保性能控制器增益:

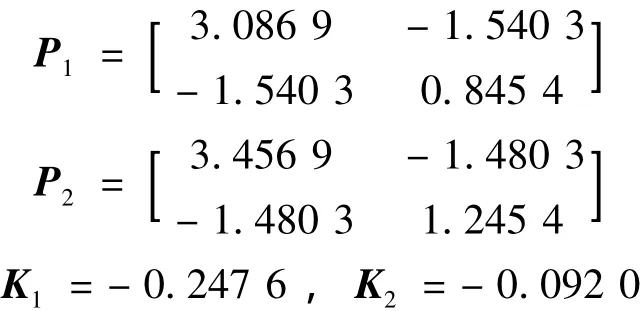
H∞性能指標γ=6.902 5。相應得到系統的一個性能上界:J*≤0.851 7。

圖1為根據定理1得到的H∞輸出反饋保性能控制器所構成閉環系統式(13)的狀態響應曲線:

圖1 根據定理1得到的系統狀態響應曲線Fig.1 State responses of the closed-loop system according to lemma 1

應用定理2得到使閉環系統式(13)具有二次D-穩定性的一個二次D-性能矩陣以及使閉環系統式(13)容許的H∞靜態輸出反饋保性能控制器增益:H∞性能指標γ=13.563。相應得到系統的一個性能上界:J*≤7.041。

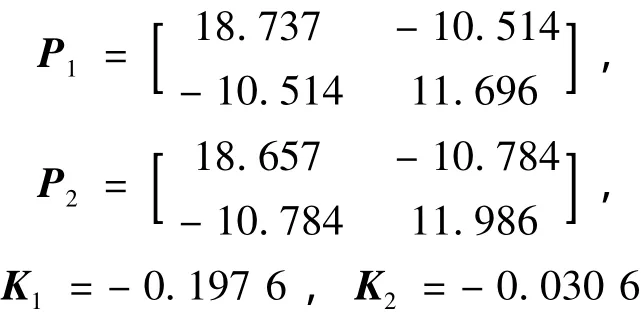
圖2為根據定理2得到的H∞輸出反饋保性能控制器所構成閉環系統式(13)的狀態響應曲線。

圖2 根據定理2得到的系統狀態響應曲線Fig.2 State responses of the closed-loop system according to lemma 2

由通過仿真所得到的數據可以看到，基于定理1所設計的控制器使得閉環系統式(13)H∞擾動抑制度γ=6.902 5，且性能上屆小于0.851 7，滿足先前的設計要求。基于定理2所設計的控制器使得閉環系統式(13)具有二次D-穩定性，同時得到系統的H∞干擾抑制度 γ=13.563，相應性能上屆為7.041。通過分析可以看到，基于定理2的控制器設計方法由于考慮了系統的二次D-穩定性使得H∞性能指標較基于定理1所得到的同類性能指標有所下降，即:閉環系統式(13)具有二次D-穩定性時魯棒性能有所下降。

下面采用一個實際例子進行說明，使用隧道二極管電路作為一個物理映射，證實對范數有界廣義分段仿射系統H∞靜態輸出反饋保性能控制器的求取［14］，定理1比定理2具有更好的系統魯棒控制性能，考慮隧道二極管電路［18］，電容電壓用x1(k)表示，電感電流用x2(k)表示，流過隧道二極管的電流用x3(k)表示。經過離散化得到離散廣義分段仿射系統模型:系統參數的取值參看文獻［14］，其余參數及橢圓區域分段按照第一個數值例子進行選擇，系統擾動輸入向量

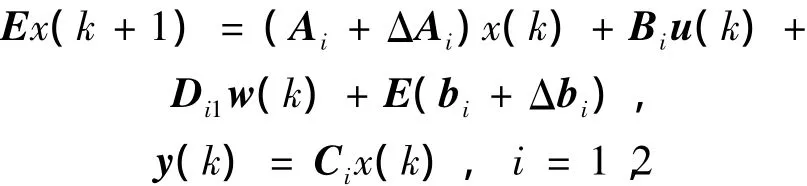
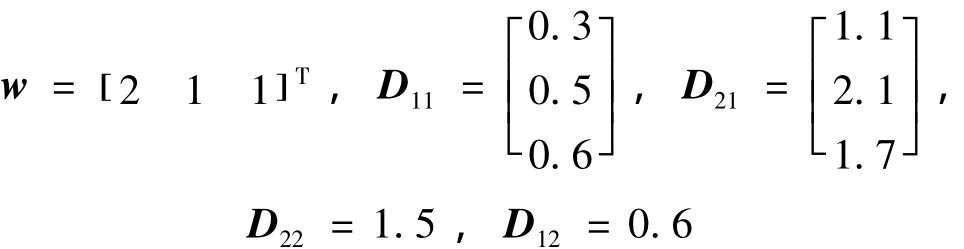
進行實驗仿真可得:基于定理2求取H∞靜態輸出反饋控制器時，利用Matlab軟件無法得到可行解。基于定理1求取廣義分段仿射系統H∞靜態輸出反饋保性能控制器增益:K1=-1.256 6，K2=-0.526 3。H∞性能指標γ=9.563。

從仿真所得數據可以看到基于定理2的控制器設計方法由于考慮了二次D-穩定性使得閉環系統魯棒性能有所下降。

4 結束語

本文在分段仿射Lyapunov函數，投影定理以及幾個處理線性矩陣不等式基本引理的基礎上，設計了使具有范數有界形式參數不確定性的離散時間廣義分段仿射系統容許的H∞輸出反饋保性能控制器，保證了由此構成的閉環系統具有二次D-穩定性。控制器存在的充分條件在所采用算法的基礎上最終體現為LMIs約束的形式，并且求解過程不包含對系統矩陣的分解，這種做法大大減低了算法的保守性，最后的數值仿真給出了H∞靜態輸出反饋保性能控制器的最優解，同時使得閉環系統極點被約束在復平面指定區域上，并注意到由于考慮系統的二次D-穩定性使得系統原本H∞性能指標有所下降。仿真證明了設計方法的有效性。

［1］MASUBUCHI，KAMITANE Y，OHARA A.H∞control for descriptor systems:amatrix inequalities approach［J］.Automatica，1997，33(4):669-673.

［2］De OLIVEIRA M C，GEROMEL JC.A class of robust stability conditions where linear parameter dependence of the Lyapunov function is a necessary condition for arbitrary parameter dependence［J］.Systems Control Letters，2005，54:1131-1134.

［3］QIU J，FENG G，GAO H.Approaches to robust H∞static output feedback control of discrete-time piecewise-affine systems with norm-bounded uncertainties［J］.Int J Robust Nonlinear Control，2011，21:790-814.

［4］PERESP L D，GEROMEl JC.H∞guaranteed cost control for uncertain continuous-time linear systems［J］.Systems and Control Letters，1993，20:413-418.

［5］DAAFOUZ J，BERNUSSOU J.Poly-quadratic stability and H∞performance for discrete systems with time varying uncertainties［C］//Proceedings of the 40th IEEE Conference on Decision and Control.Orlando，FL，USA，2001:267-272.

［6］GEROMEL JC，OLIVEIRA de M C，BERNUSSOU J.Robust filtering of discrete-time linear systems with parameter dependent Lyapunov functions［J］.SIAM JControl Optim，2002，41(3):700-711.

［7］LEITE V JS，PERES P L D.An improved LMI condition for robust D-stability of uncertain polytopic systems［J］.IEEE Trans Automat Control，2003，48(3):500-504.

［8］KIM JH.Delay-dependent robust and non-fragile guaranteed cost control for uncertain singular systems with time-varying state and input delays［J］.International Journal of Control，Automation，and Systems，2009，7(3):357-364.

［9］REN Junsheng，ZHANG Xianku.Guaranteed cost control of nonlinear singular system with time delays using T-S Fuzzy model［J］.Applied Mathematics ＆ Information Sciences，2013，7(4):1615-1622.

［10］ZHU X L，YANGG H.Integral inequality approach to stability analysis of continuous-time systems with time-varying delay［J］.IET Control Theory，2008，2(6):524-534.

［11］DONG J，YANG G H.Robust static output feedback control for linear discrete-time systems with time-varying uncertainties［J］.Systems and Control Letters，2008，57(2):123-131.

［12］BARBOSA K A，SOUZA C E de.Robust H∞filtering for discrete-time with uncertainty nonlinear systems using parameter-dependent Lyapunov functions［C］//Proceedings of the American Control Conference.Alaska，USA，2002:3224-3229.

［13］DONG J，YANG G H.Static output feedback control synthesis for linear systems with time-invariant parametric uncertainties［J］.IEEE Transactions on Automatic Control，2007，52(10):1930-1936.

［14］WANG Mao，WEI Yanling，QIU Jianbin.Static output feedback control of discrete-time piecewise affine singular systems［J］.Journal of Harbin Institute of Technology，2013，45(3):14-21.

［15］HSIUNG K L，LEE L.Lyapunov inequality and bounded real lemma for discrete-time descriptor systems［J］.IEEE Proc-Control Theory，1999，146(4):327-331.

［16］杜寶珠.不確定廣義系統的保性能控制［D］.沈陽:東北大學，2006:37-40.DU Baozhu.Guaranteed cost control for uncertain singular systems［J］.Shenyang:Northeastern University，2006:37-40.

［17］BOYD S，EL G L，FERON E，et al.Linearmatrix inequality in systems and control theory［M］.SIAM:Philadelphia，PA，1994.

［18］RODRIGUES L，BOYD S.Piecewise-affine state feedback for piecewise-affine slab systems using convex optimization［J］.Systems and Control Letters，2005，54(9):835-853.