彈性支撐階梯柱側(cè)向位移與穩(wěn)定性的精確分析

都亮，陸念力，蘭朋

(哈爾濱工業(yè)大學(xué)機(jī)電工程學(xué)院，黑龍江哈爾濱150001)

在工程起重機(jī)、鋼結(jié)構(gòu)橋梁、以及房屋建筑中，為合理地利用材料和減輕重量，梁柱的截面經(jīng)常沿軸向發(fā)生變化，呈階梯柱或截面連續(xù)變化的形式。對(duì)于該類(lèi)結(jié)構(gòu)的穩(wěn)定性問(wèn)題，許多學(xué)者進(jìn)行了深入研究［1-4］。中國(guó)起重機(jī)設(shè)計(jì)規(guī)范 GB/T3811-2008中，起重機(jī)伸縮臂的失穩(wěn)計(jì)算模型為變截面梯形柱［5］，其失穩(wěn)臨界力采用精確有限元法計(jì)算得到［6］。但上述研究均將假設(shè)邊界約束條件為剛性或鉸接，實(shí)際工程中箱形伸縮臂的邊界約束條件并非完全鉸接或固支，往往具有一定的彈性［7-9］。Timoshenko和Iyengar等對(duì)具有彈性約束的等截面梁屈曲問(wèn)題進(jìn)行了研究［1，10］。陸念力等［11］就兩端彈性約束簡(jiǎn)支等截面壓彎梁和彈性嵌固等截面懸臂壓彎梁進(jìn)行了分析;Vaziri等［12］研究了非均布軸向載荷作用下變截面梁柱的屈曲問(wèn)題。LIQ S等［13-14］利用一系列等截面構(gòu)件逼近的方法，提出了一種用于具有端部彈性支撐和分布力共同作用的變截面梁柱的穩(wěn)定性分析方法并給出了具有特定形狀的無(wú)側(cè)向約束變截面懸臂梁穩(wěn)定性分析的精確解析解。

本文針對(duì)端部彈性約束的變截面階梯柱模型，通過(guò)微分方程法，基于二階效應(yīng)在變形后位形上建立平衡方程，得到頂端撓度精確解析表達(dá)式和失穩(wěn)特征方程的精確遞推公式，從而獲取屈曲臨界力。

1 計(jì)及二階效應(yīng)的彈性支撐變截面階梯柱失穩(wěn)特征方程

圖1(a)所示的油缸變幅箱形伸縮臂平面內(nèi)受力模型，假設(shè)變幅油缸剛度無(wú)窮大，則伸縮臂l0段連同變幅油缸可以等效為如圖1(b)所示的轉(zhuǎn)動(dòng)剛度K0，則1(a)所示的箱形伸縮臂平面內(nèi)剛度與穩(wěn)定性問(wèn)題轉(zhuǎn)化為彈性約束下箱形伸縮臂側(cè)向剛度與縱向穩(wěn)定性問(wèn)題。首先以圖1(b)所示的彈性約束情況下變截面階梯柱模型為研究對(duì)象進(jìn)行剛度與穩(wěn)定性分析。設(shè)各節(jié)臂截面慣性矩為Ii(i=1，2，3…n)，階梯柱承受頂端彎矩M，側(cè)向力Q和軸向力P，則其基于縱橫彎曲理論建立的各節(jié)臂撓曲微分方程列為

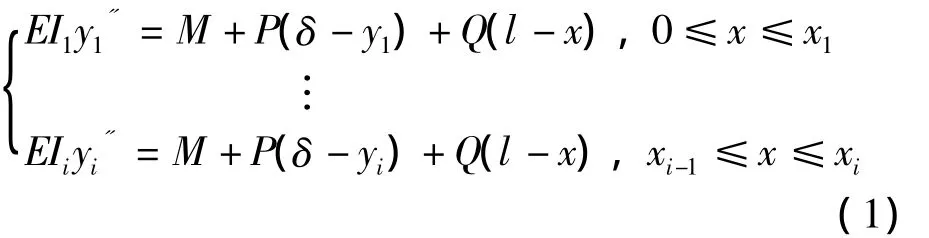
上式可統(tǒng)一表示為

式中:k=

i。方程(2)的通解為

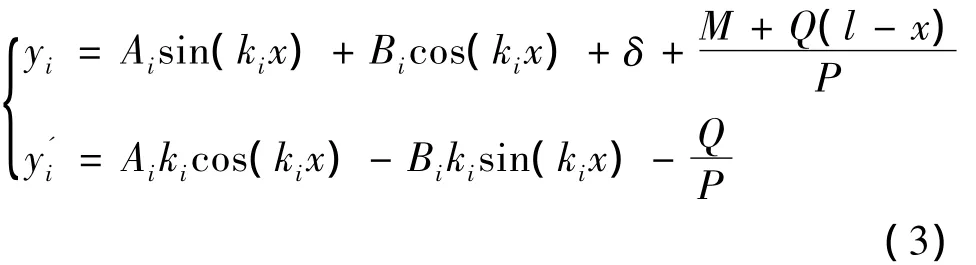
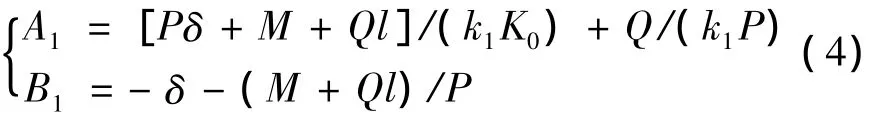
由x=xi時(shí)各段連接處變形諧調(diào)條件:yi=yi+1，＇=yi+1＇，得到

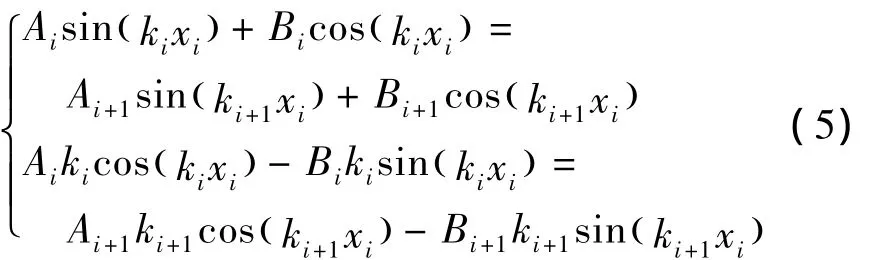
將式(5)用矩陣形式表達(dá)為

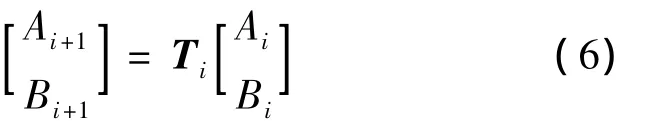
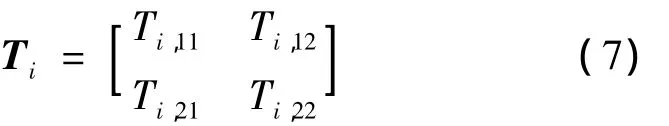
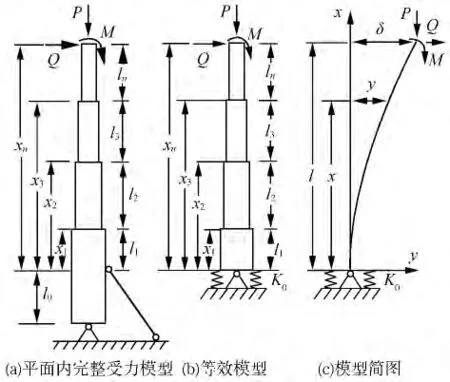
圖1 起重機(jī)伸縮臂及等效彈性支撐階梯柱模型Fig.1 M odel of crane telescopic boom and stepped colum n with elastically restrained

式中:

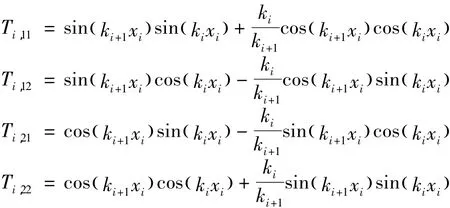
因此可得到積分常數(shù)An和Bn的遞推表達(dá)式:

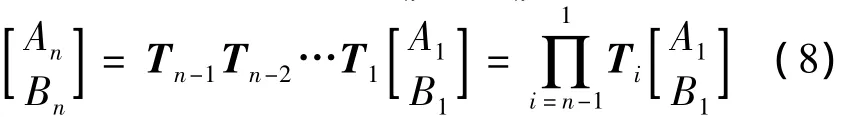
又由x=xn=l時(shí)伸縮臂頂部條件yn=δ得

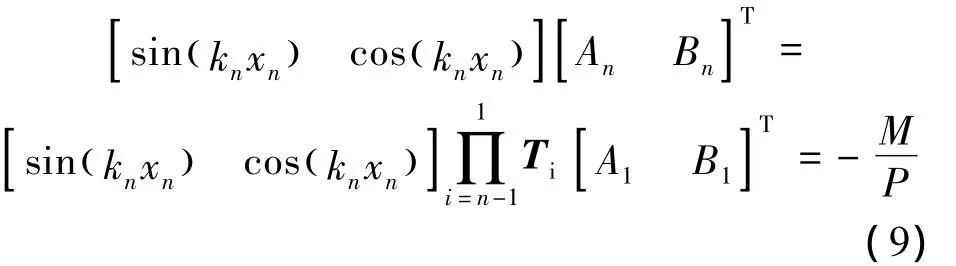
將式(4)中 A1、B1代入式(9)得

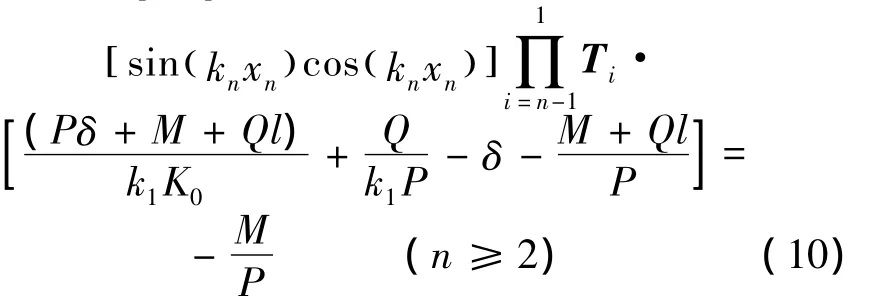
求解式(10)可得階梯柱自由端部撓度δ:

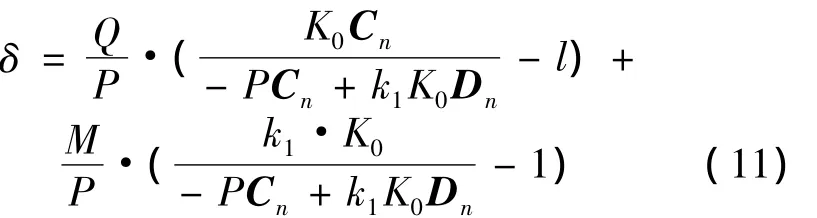
式中:

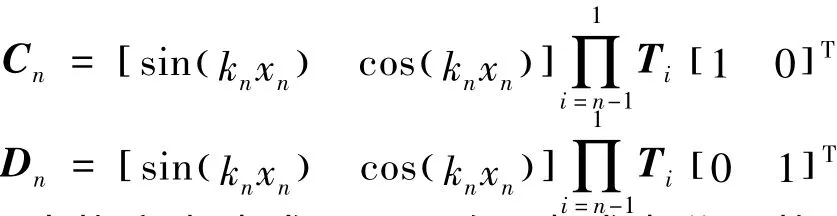
由撓度表達(dá)式(11)可知，當(dāng)式中分母趨于0時(shí)，對(duì)應(yīng)的撓度表達(dá)式皆表現(xiàn)為0/0不定式或者無(wú)窮大，結(jié)構(gòu)失穩(wěn)，從而有失穩(wěn)特征方程:

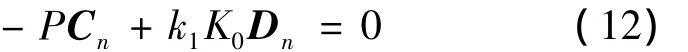
若K0已知，式(12)是以ki為未知量的非線性超越方程，解此方程可得結(jié)構(gòu)失穩(wěn)臨界力:

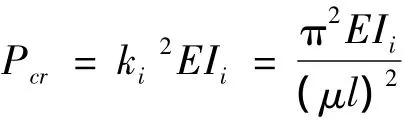
2 平面內(nèi)失穩(wěn)特征方程的顯式表達(dá)

前述得出的失穩(wěn)特征方程涉及到根部轉(zhuǎn)動(dòng)剛度K0，該轉(zhuǎn)動(dòng)剛度可由圖1(a)模型中油缸支撐段求得。文獻(xiàn)［1］給出長(zhǎng)度為l0的兩端鉸接壓彎柱在一端受力矩為M時(shí)的柱端轉(zhuǎn)角:

當(dāng)令M=1，得到柱端柔度，其倒數(shù)即為對(duì)應(yīng)的轉(zhuǎn)動(dòng)剛度:

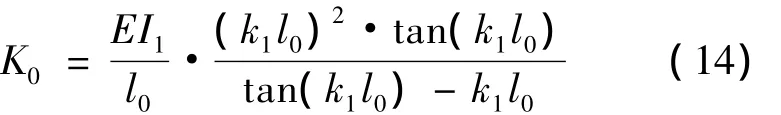
將此彈性支撐階梯柱根部等效剛度K0的表達(dá)式代入失穩(wěn)特征方程，可得到伸縮臂平面內(nèi)失穩(wěn)特征方程的完整精確表達(dá)。顯然彈性約束伸縮臂的臨界力取決于臂節(jié)幾何參數(shù)及臂節(jié)數(shù)n，式(15)～(19)給出了工程中常見(jiàn)的5節(jié)以?xún)?nèi)起重機(jī)伸縮臂失穩(wěn)特征方程的顯式表達(dá)。

當(dāng)n=1時(shí)，失穩(wěn)特征方程式(12)可表示為

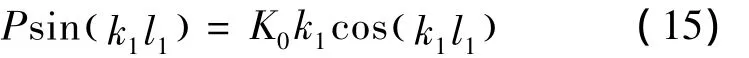
當(dāng)n=2時(shí)，起重臂的失穩(wěn)特征方程可表示為

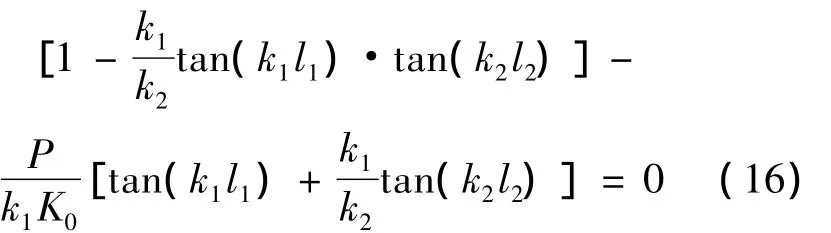
當(dāng)n=3時(shí)，起重臂的失穩(wěn)特征方程可表示為

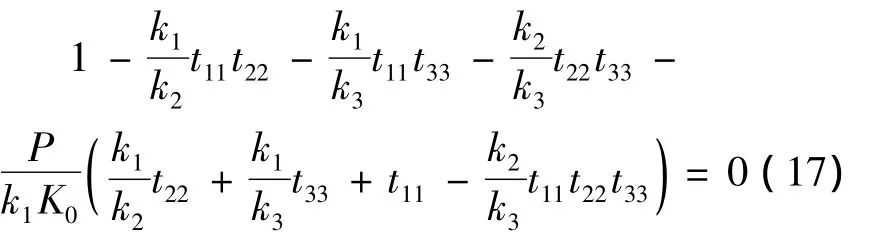
當(dāng)n=4時(shí)，起重臂的失穩(wěn)特征方程可表示為

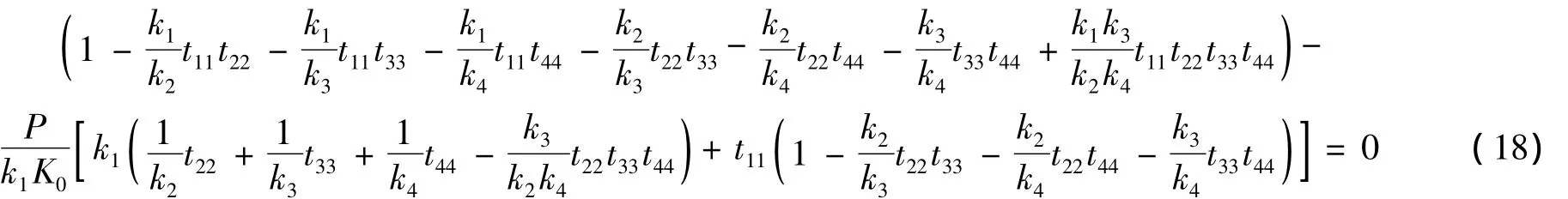
當(dāng)n=5時(shí)，起重臂的失穩(wěn)特征方程可表示為

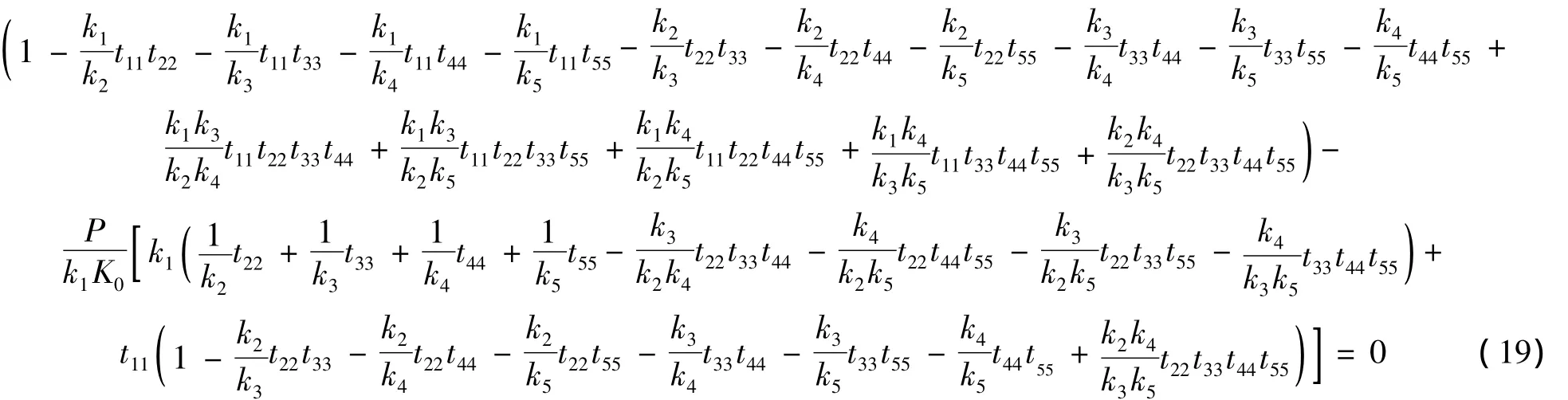
以上各式中采用符號(hào)tii=tan(kili)，li表示各節(jié)伸縮臂的長(zhǎng)度，li=xi-xi-1，l1=x1，l=xn。

3 根部約束四級(jí)階梯柱分析算例

應(yīng)用前文得到的方法，對(duì)圖2所示根部彈性約束四節(jié)臂變截面階梯柱進(jìn)行撓度與臨界力計(jì)算。用有限元軟件ANSYS分析對(duì)比，將每節(jié)臂分為10個(gè)單元計(jì)算，比較驗(yàn)證方法的精度與準(zhǔn)確性。

如圖2所示具有彈性約束的變截面階梯柱，彈性模量E=206 GPa，階梯柱長(zhǎng)L=10 m，a1=0.34，a2=0.56，a3=0.78，I4=3.58 ×10-6m4，I1=2.2I2，I2=1.9I3，I3=1.3I4;載荷 Q=500 N，M=1 kN·m，P=5 kN 。

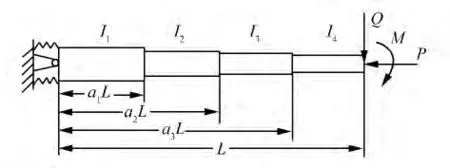
圖2 四節(jié)臂彈性支撐變截面階梯柱模型Fig.2 Model of four sectioned stepped column

以下將從2個(gè)方面對(duì)本文方法進(jìn)行驗(yàn)證:

1)彈性支撐變截面階梯柱之變形驗(yàn)證。引入無(wú)量綱彈性嵌固系數(shù)ξ=K0l/(EI1)，在不同彈性嵌固系數(shù)下，計(jì)算結(jié)果列于表1。由表中可見(jiàn)，所得計(jì)算結(jié)果與ANSYS幾無(wú)差別。通過(guò)與ANSYS線性解即不考慮二階效應(yīng)時(shí)結(jié)果的比較，表明二階效應(yīng)對(duì)側(cè)向剛度的影響。

2)彈性支撐變截面階梯柱之屈曲驗(yàn)證。表2給出了不同彈性支撐情況下變截面階梯柱臨界力的計(jì)算長(zhǎng)度系數(shù)μ值。計(jì)算結(jié)果與ANSYS分析結(jié)果完全一致。

表1 具有彈性約束的變截面階梯柱自由端撓度Table 1 The deflection of variable cross-section stepped column with elastically restrained

表2 具有彈性約束的變截面階梯柱的計(jì)算長(zhǎng)度系數(shù)μ值Tab le 2 The effective length factorμ of variable cross-section stepped column with elastically restrained

4 結(jié)束語(yǔ)

本文對(duì)箱形伸縮臂平面內(nèi)的受力模型進(jìn)行了合理等效，得到了彈性約束條件下變截面階梯柱失穩(wěn)計(jì)算模型，彈性約束下變截面階梯柱屈曲特征方程的精確遞推公式。通過(guò)本文方法與ANSYS對(duì)實(shí)際算例進(jìn)行分析比較發(fā)現(xiàn)，兩者得到的穩(wěn)定性分析結(jié)果完全一致，且在進(jìn)行非線性撓度分析時(shí)誤差隨著彈性約束的剛度增加而逐漸減小，對(duì)于本文給出的實(shí)際模型其最大誤差小于0.002%;ANSYS線性分析結(jié)果與本文非線性結(jié)果最大誤差達(dá)19.8%，遠(yuǎn)超過(guò)工程應(yīng)用5%的誤差允許范圍。算例表明本文針對(duì)彈性約束的變截面階梯柱剛度與穩(wěn)定性問(wèn)題的理論推導(dǎo)是正確和必需的。

［1］TIMOSHENKO SP，GERE JM.Theory of elastic stability［M］.2nd ed.New York:McGraw-Hill，1961:100-116.

［2］ZHANG Hongsheng，LU Nianli，LAN Peng.Buckling of stepped beams with elastic supports［J］.Journal of Harbin Institute of Technology，2009，16(3):436-440.

［3］張氫，盧耀祖，石來(lái)德.承受大噸位載荷的門(mén)框形立柱穩(wěn)定性分析［J］.同濟(jì)大學(xué)學(xué)報(bào)，2003，31(9):1068-1073.ZHANG Qing，LU Yaozu，SHILaide.Nolinear buckling analysis of potal frames with large work loads［J］.Journal of Tongji University，2003，31(9):1068-1071.

［4］PARK JS，STALLINGS JM.Lateral-torsional buckling of stepped beams with continuous bracing［J］.Journal of Bridge Engineering，2005，10(1):87-95.

［5］全國(guó)起重機(jī)械標(biāo)準(zhǔn)化技術(shù)委員會(huì).GB/T3811-2008，起重機(jī)設(shè)計(jì)規(guī)范［S］.北京:中國(guó)標(biāo)準(zhǔn)出版社，2008.

［6］陸念力，蘭朋，白樺.起重機(jī)箱形伸縮臂穩(wěn)定性分析的精確理論解［J］.哈爾濱建筑大學(xué)學(xué)報(bào)，2000，33(2):89-93.LU Nianli，LAN Peng，BAIHua.Precise stability analysis of telescopic boom［J］.Journal of Harbin University of Civil Engineering and Architecture，2000，33(4):89-93.

［7］陸念力，孟麗霞.基于二階理論的彈性約束變截面懸臂梁剛度與穩(wěn)定性分析［J］.工程力學(xué)，2012，29(12):365-369.LU Nianli，MENG Lixia.The stiffness and stability analysis of a tapered beam with elastic restraint considering secondorder effects［J］.Engineering Mechanics，2012，29(12):365-369.

［8］LEE S Y，KUO Y H.Elastic stability of non-uniform columns［J］.Sound Vibration，1991，148(1):11-24.

［9］LI Q S，CAO H，LI G.Static and dynamic analysis of straight bars with variable cross-section［J］.Comput and Struct，1996，59:1185-1191.

［10］IYENGAR NG R.Structural stability of columns and plates［M］.New York:John Wiley and Sons，1988:40-55.

［11］陸念力，羅冰，夏擁軍.基于二階理論的兩端彈性約束壓彎梁的穩(wěn)定性分析和最大彎矩計(jì)算［J］.起重運(yùn)輸機(jī)械，2009(5):8-11.LU Nianli，LUO Bing，XIA Yongjun.Stability analysis and maximum bending moment calculation of free beam with elastic constrains at both ends based on second-order theory［J］.Hoisting and Conveying Machinery，2009(5):8-11.

［12］VAZIRIH H，XIE J.Buckling of columns under variably distributed axial loads［J］.Comput Struct，1992，45(3):505-509.

［13］LIQ S.Buckling analysis of multi-step non-uniform beams［J］.Adv Struct Engng，2000，3(2):139-144.

［14］LIQ S.Buckling of multi-step non-uniform beams with elastically restrained boundary conditions［J］.Journal of Constructional Steel Research，2001，57(7):753-777.