三階非線性三點邊值問題的正解

孔令彬，金前德

(東北石油大學數學與統計學院，黑龍江大慶 163318)

三階非線性三點邊值問題的正解

孔令彬，金前德

(東北石油大學數學與統計學院，黑龍江大慶 163318)

利用Krasnoselskii不動點定理及Ascoli-Arzela定理，研究含參數的非線性三階三點邊值問題，證明當參數取值范圍不同時，該邊值問題的正解存在性與不存在性.

非線性三階三點邊值問題；存在性；正解

0 引言

非線性三階三點邊值問題來源于應用數學與物理等領域，已受到人們重視和研究[1-15].Sun Y在文獻[16]研究下述非線性三階三點邊值問題，即

式(3)、(4)較式(1)、(2)更一般些.當ρ=0時，式(3)、(4)與式(1)、(2)相類似，可采用文獻[16]的方法考慮正解存在性.筆者考慮ρ＞0情形，通過適當變換，再利用Krasnoselskii不動點定理和Ascoli-Arzela定理，討論參數變化時式(3)、(4)是否存在正解，所采用的方法與文獻[16]不同，獲得新結果.

假設：

(H1)對每個固定的u∈[0，+∞)，f(t，u)在t∈[0，1]上非負連續，對幾乎所有的t∈[0，1]，f(t，u)關于u≥0單調非增；

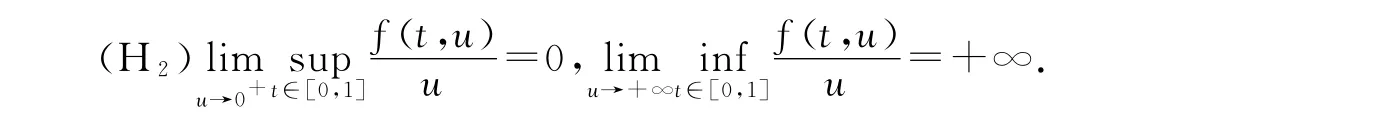
定義 稱函數u(t)為式(3)、(4)的一個正解，如果它滿足

(ⅰ)u∈C1[0，1]∩C2(0，1)并在(0，1)內u(t)＞0；

(ⅱ)u(t)滿足式(3)和式(4).

主要結論為

定理1 假設(H1)、(H2)成立，則存在λ*∈(0，+∞).當λ∈(0，λ*]時，式(3)、(4)至少存在一個正解；當λ∈(λ*，+∞)時，式(3)，(4)不存在正解.

1 式(3)、(4)的等價形式及預備引理

設C[0，1]是[0，1]上連續函數構成的Banach空間，C+[0，1]={v∈C[0，1]；v(t)≥0}，定義映射J：C+[0，1]→C+[0，1]，則

容易知道，若u(t)滿足式(3)、(4)，令u′(t)+ρu(t)=-v(t)，則v(t)滿足式(6)、(7)，其中Jv(t)由式(5)給出.反之，若v(t)滿足式(6)、(7)，令u(t)=Jv(t)，則u(t)滿足式(3)、(4)，因此邊值問題式(3)、(4)與邊值問題式(6)、(7)等價.

為證明文中主要結論，給出5個引理.

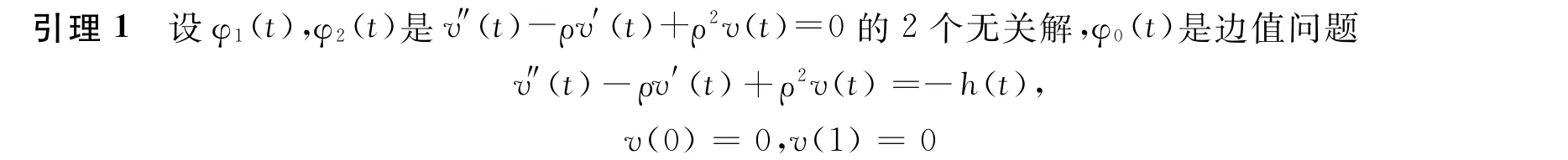
的解，則v″(t)-ρv′(t)+ρ2v(t)=-h(t)的任何解可表示為v(t)=C1φ1(t)+C2φ2(t)+φ0(t)，其中h∈C+[0，1]，C1，C2是任意常數.

證明 直接驗證即可.

2 定理1的證明

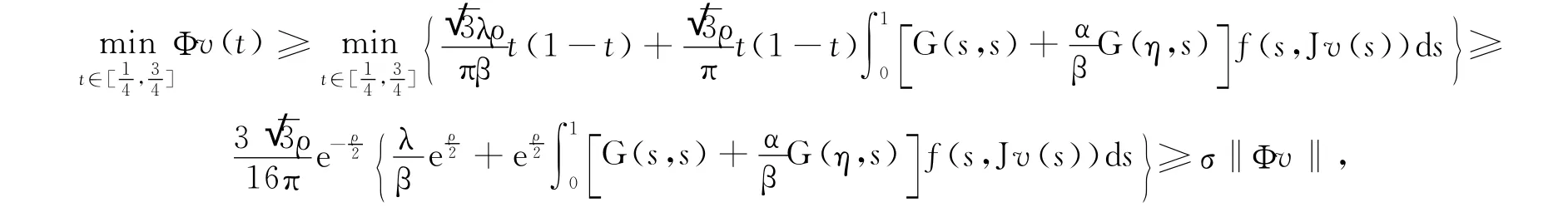
即Φv∈K或Φ(K)?K.另外，易證Φ是全連續的.

引理7 假設(H1)、(H2)成立，若λ充分大，則式(6)、(7)無正解.

3 結束語

研究含參數的非線性三階邊值問題，給出該問題的Green函數，進而將該邊值問題轉化為等價的積分方程，在適當的空間上定義映射，通過利用Green函數的性質和錐不動點定理，證明正解的存在性.

[1] Graef J R，Yang B.Multiple positive solutions to a three point third order boundary value problem[J].Discrete Contin.Dyn.Syst，2005(S1)：1-8.

[2] Guo L，Sun J，Zhao Y.Existence of positive solution for nonlinear third-order three point boundary value problem[J].Nonlinear A-nal，2007(14)：93-111.

[3] Boucherif A，Al-Malki N.Nonlinear three-point third order boundary value problems[J].Appl.Math.Comput，2007(190)：1168-1177.

[4] Sun Y.Positive solutions of singular third order three point boundary value problems[J].J.Math.Anal.Appl，2005(306)：589-603.

[5] Yu H，Lu H，Liu Y.Multiple positive solutions to third-order three-point singular semi positive boundary value problem[J].Proc. Indian Acad.Sci.Math.Sci，2004(114)：409-422.

[6] Guo L J，Sun J P，Zhao Y H.Existence of positive solutions for nonlinear third-order three-point boundary value problems[J].Nonlinear Anal，2008(68)：3151-3158.

[7] Graef J R，Webb J R.Third order boundary value problems with nonlocal boundary conditions[J].Nonlinear Anal，2009(71)：1542-1551.

[8] Graef J R，Yang B.Positive solutions of a third order nonlocal boundary value problem[J].Discrete Contin.Dyn.Syst.Ser，2008 (S1)：89-97.

[9] Stanek S.On a three-point boundary value problem for third order differential equations with singularities in phase variables[J]. Georgian Math.J，2007(14)：361-383.

[10] Graef J R，Henderson J，Wong P J，et al.Three positive solutions of an n-th order three point focal type boundary value problem[J]. Nonlinear Anal，2008(69)：3386-3404.

[11] Erbe L H，Wang H.On the existence of positive solutions of ordinary differential equations[J].Proc.Amer.Math，1994(120)：743 -748.

[12] 孫建平，張小麗.非線性三階三點邊值問題正解的存在性[J].西北師范大學學報：自然科學版，2012，48(3)：14-21.

Zhang Jianpin，Zhang Xiaoli.Existence of positive solutions for a class of third-order Three-point boundary value problem[J].Journal of Northwest Normal University：Natural Science Edition，2012，48(3)：14-21.

[13] 張立新，孫博，張洪.三點邊值問題的兩個正解的存在性[J].西南師范大學學報：自然學科版，2013，16(10)：30-33.

Zhang Lixin，Sun Bo，Zhang Hong.Existence of two positive solution for three-point third order boundary value problems[J].Journal of Southwest China Normal University：Natural Science Edition，2013，16(10)：30-33.

[14] 姚慶六.一類復合型奇異三階三點邊值問題正解的存在性[J].浙江大學學報：理學版，2012，39(4)：381-384.

Yao Qingliu.Existence of positive solution for a kind of composite singular three order three point boundary value problem[J].Journal of Zhejiang University：Science Edition，2012，39(4)：381-384.

[15] 張曉萍，孫永平.三階三點邊值問題正解的存在性[J].數學的實踐與認識，2014，44(2)：181-185.

Zhang Xiaoping，Sun Yongping.Existence of positive solutions for a class of third-order three-point boundary value problem[J]. Mathematics in Practice and Theory，2014，44(2)：181-185.

[16] Sun Y.Positive solutions for third-order three-point nonhomogeneous boundary value problems[J].Appl.Math.Lett，2009(22)：45-51.

O175.8

A

2095-4107(2014)05-0121-06

DOI 10.3969/j.issn.2095-4107.2014.04.015

2014-04-09；編輯關開澄

黑龍江省教育廳科學技術研究項目(12541076)

孔令彬(1956-)男，碩士，教授，主要從事非線性微分方程邊值問題方面的研究.