金水溝特大橋彈塑性抗震分析

岳迎九

(中鐵第一勘察設計院集團有限公司橋隧處， 西安 710043)

金水溝特大橋彈塑性抗震分析

岳迎九

(中鐵第一勘察設計院集團有限公司橋隧處， 西安 710043)

為了深入了解高墩大跨預應力混凝土剛構連續梁橋在罕遇地震下結構的反應特征，利用Midas/Civil軟件，混凝土和鋼筋分別采用Mander本構關系和修正梅內戈托與平托本構關系，建立結構的纖維模型，對金水溝特大橋進行罕遇地震下的彈塑性抗震分析。分析結果表明，纖維模型可以有效模擬結構地震下的反應，在罕遇地震下的強度與變形均滿足規范，滿足“大震不倒”的抗震設防要求，并且還有一定的安全儲備；對于金水溝這類高墩大跨剛構連續梁橋，橫橋向墩底為控制截面，順橋向連續梁墩墩底、剛構墩的墩頂與墩底均為控制截面，并且結構順橋向的地震力較橫橋向更為控制結構設計。

剛構連續梁橋；纖維模型；罕遇地震；彈塑性抗震分析；本構模型

1 概述

鋼筋混凝土結構的抗震分析方法，經歷了從靜力到動力，從線性到非線性，由彈性到彈塑性的發展過程[1]。并且隨著社會的進步與科技的發展，抗震分析手段也取得了長足的進步，利用計算機基于一些專業軟件，可以模擬復雜結構在地震力作用的反應。目前，對于比較重要的大型結構，一般要求對結構在罕遇地震下的抗震性能做出評價，即對結構進行罕遇地震下的非線性動力彈塑性時程分析。

在橋梁分析中，常用的彈塑性有限元方法，有基于集中鉸模型的桿系有限元法和基于纖維模型的桿系有限元法。基于集中鉸模型的桿系有限元分析方法需要預先定義塑性鉸及其位置，并給定塑性鉸的滯回曲線。這種分析模型雖然應用廣泛，但是存在一些問題：一是塑性鉸長度取值各國規范計算的值往往差異顯著，二是塑性鉸的滯回曲線關系往往需要基于大量的試驗結果，還有就是模型不能考慮構件軸力與彎矩之間的相互關系。基于纖維模型的桿系有限元分析方法，是將桿件截面劃分成若干纖維，每個纖維均為單軸受力，并用材料單軸應力應變關系來描述該纖維的受力特性，纖維間的變形協調采用平截面假定。對于長細比較大的鋼筋混凝土桿系結構，纖維模型有以下優點：纖維模型將構件截面劃分為若干混凝土纖維和鋼筋纖維，通過用戶自定義每根纖維的截面位置、面積和材料的本構模型，可適用于各種截面形狀；纖維模型可以準確考慮軸力和單向或雙向彎矩的相互關系；通過采用受橫向約束的混凝土單軸應力應變本構模型，可以考慮在箍筋等橫向約束作用下對構件恢復力特性的影響[2]。因此，基于纖維模型的結構彈塑性分析在結構抗震分析中的應用越來越廣泛。

2 工程實例

位于西北地區黃土沖溝內的金水溝鐵路特大橋，其主橋孔跨布置為(80+3×140+80) m，聯長581.8 m，主橋3、4號主墩為剛構墩，2、5號次主墩及1、6號邊墩為連續梁墩，整體結構為剛構連續梁橋。橋面與地面的最大高程差約93 m，3、4號墩墩高均為80 m，2、5號墩高均為55 m，立面布置如圖1所示。橋址處的地震動峰值加速度值為0.152g，相當于地震基本烈度7度，地震動反應譜特征周期為0.43 s。由于主橋墩高聯長，屬于技術復雜、修復困難的特殊結構橋梁[3]，并且地震動峰值加速度為0.152g，需對全橋進行專門的抗震分析，對其在罕遇地震下的抗震性能做出評價。為了更真實地模擬主橋整個結構在地震下的反應，擬采用基于纖維模型的動力彈塑性時程分析方法，分析結構在罕遇地震下的抗震性能。

3 本構模型

目前，關于混凝土與鋼筋的本構模型眾多，本構模型的選取影響計算分析的可信度，應根據結構的特點，選取最適用本橋的常用本構模型。

3.1 混凝土本構模型

混凝土模型應考慮縱向鋼筋特別是箍筋對其的約束作用，由于提供結構延性的橋墩截面為異型，并且結合公路抗震規范[4]中混凝土極限壓應變公式的選取，選用Mander模型(圖2)作為混凝土的本構關系模型[5]，公式具體形式如下。

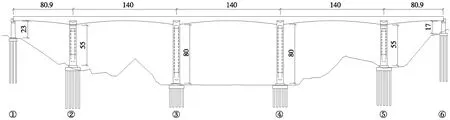
圖1 主橋孔跨布置(單位：m)

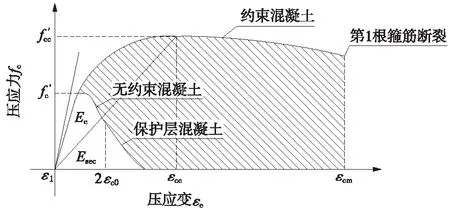
圖2 Mander混凝土纖維本構模型

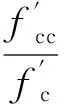
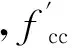
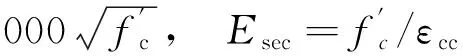
3.2 鋼筋本構模型

鋼材的本構模型采用使用最為廣泛的修正梅內戈托與平托模型(Modified Menegotto & Pinto Steel Model)[6]，本模型(圖3)具有計算效率高、與試驗結果吻合較好的特點。本構模型形狀為逐漸逼近按照隨動硬化(kinematic hardening)準則定義的雙折線的曲線，各加載路徑和應變-硬化區間的漸進線之間的轉移區段呈曲線狀態。2條漸進線的交點和卸載方向上最大應變點之間的距離越遠，轉移區段的曲線越光滑。 可利用這樣的特性模擬包辛格效應，該種本構關系可用下列公式確定[7]。

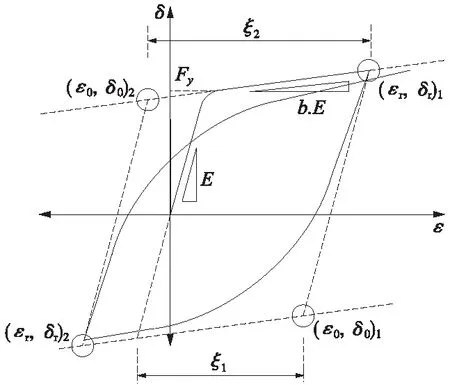
圖3 鋼材纖維本構模型

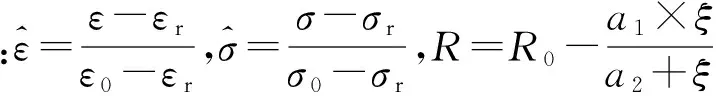
式中，ε表示鋼纖維的應變；σ表示鋼纖維的應力； (εr，σr)為卸載點，在初始彈性狀態時假設為(0， 0)；(ε0，σ0)定義當前加載或卸載路徑的2條漸進線的交點；b為剛度折減率；R0，a1，a2為常量；ξ為荷載加載或卸載方向上的最大應變與ε0的差值(絕對值)，最大應變的初始值設定與±(Fy/E)相同。

4 彈塑性抗震分析

4.1 模型的建立

采用Midas/Civil 2010橋梁有限元軟件，建立主橋結構的有限元模型。主梁采用一般空間梁單元，橋墩采用纖維桿系單元。MIDAS/Civil中彈塑性纖維梁單元使用了下面的幾個假定：基于幾何線性小變形假定；滿足平截面假定；鋼筋與混凝土粘結良好，忽略粘結滑移和剪切滑移影響；剪切變形是彈性的[8]。鋼筋混凝土桿件截面可以被劃分成約束混凝土纖維、非約束混凝土纖維以及鋼筋纖維，纖維材料的非線性特性可采用上節中混凝土與鋼筋的本構關系來體現[9]。圖4給出了劃分好的纖維截面，截面中的點即為按照實際鋼筋的直徑與間距定義的鋼筋纖維，方格為劃分的混凝土纖維。

圖4 橋墩截面纖維劃分

用M法計算樁基對承臺的彈性支承剛度[10]，在模型承臺底加上6個自由度的彈性支承[11]，全橋整體計算模型如圖5所示。

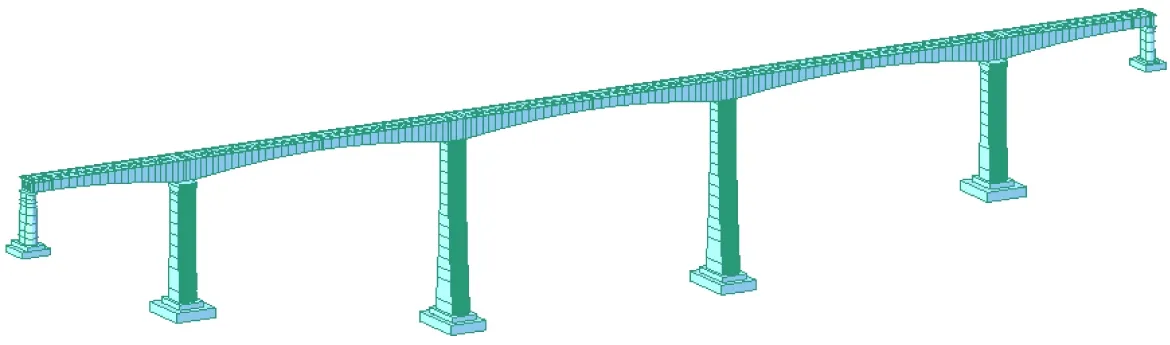
圖5 計算模型

4.2 地震波來源

由于主橋結構的特殊性，對其橋址區做了專門的地震安全性評價工作。采用擬合基巖反應譜的三角級數迭加法合成場地基巖地震動時程，給出了50年超越概率63%、10%和2%三種設防概率水平的合成場地基巖地震動加速度時程，每種概率水平各給出了3條加速度時程。由于本橋墩高聯長，屬于修復困難的重點橋渡，并且橋址屬于0.15g的7度區，因此擬采用3條超越概率2%的人工合成波，來進行全橋的地震反應分析。圖6僅示出了50年超越概率為2%的一條時程曲線。

5 計算結果分析

將50年超越概率為2%的3條時程曲線分別輸入，在Midas中采用直接積分法，得到罕遇地震下順橋及橫橋向主橋的地震反應。當采用3條時程波計算時，時程分析的最終結果應取3組計算結果的最大值[4]。

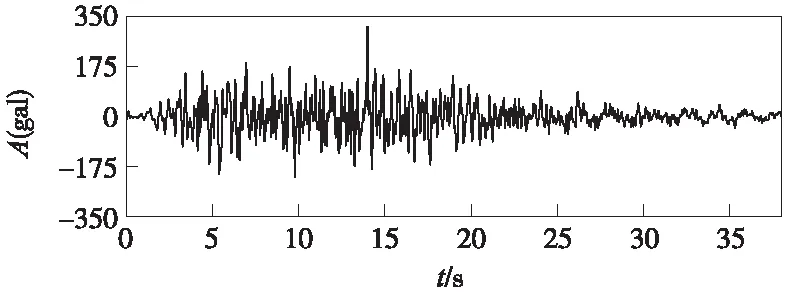
圖6 水平地震動時程曲線(2%)

5.1 截面特性分析結果

先求出纖維截面在地震力下所受的軸力，在Midas中可以直接得到截面的理想彈塑性軸力-彎矩-曲率(p-M-f)曲線，從中可以得到截面開裂、屈服及極限狀態下的彎矩和曲率，從而對截面的抗震性能做出初步了解。選取了9個可能出現塑性鉸的代表性截面，表1和表2分別列出了9個代表性截面在順橋向與橫橋向的截面特性。

表1 順橋向截面特性

表2 橫橋向截面特性

5.2 彈塑性地震響應分析結果

對全橋進行彈塑性地震響應分析，可以得到橋墩各纖維單元的內力及變形。對橋梁結構進行抗震性能評價，首先是評價標準的選取問題，規范一般都是對地震下結構的強度和變形做了規定。《鐵路工程抗震設計規范》[3]中，對強度概括性的要求是“大震不倒”。地震下，一般來說彎矩對強度起控制性因素。當計算彎矩未超過截面的極限彎矩或屈服彎矩時，鋼筋未達到屈服狀態，此時混凝土一般不會出現壓潰現象，可以認定此時結構未完全喪失承載力，即滿足“大震不倒”的要求。地震下結構變形過大，可加速結構喪失承載力，即使未發生倒塌，也可能危及結構上車輛及行人的安全，因此雖然延性設計中需要結構提供一定的變形能力用以消耗地震的能量，但是需要對結構的最大變形做出限制。鐵路抗震規范中，對變形的規定為延性比，即橋墩的非線性響應最大位移與屈服位移比值小于4.8。以上規定主要是針對一般單墩結構，并且是對整體變形的要求，對于本工程實例中在墩頂也可能出現塑性鉸的剛構連續梁橋并不適用。《公路橋梁抗震設計細則》[4]中規定，在E2地震作用下，潛在塑性鉸區域的塑性轉角θp，應小于等于塑性鉸區域的最大允許轉角θu。顯然，公路規范的規定更加適合，因此選用公路規范中的規定來作為結構的變形控制條件。表3與表4分別給出了橋墩9個截面順橋向與橫橋向罕遇地震下的最大彎矩與最大轉角。

表3 順橋向截面彎矩與轉角

由表3看出，所選截面順橋向的計算彎矩均超過開裂彎矩但未達到屈服彎矩，說明橋墩在罕遇地震下混凝土發生開裂，結構進入塑性狀態，但是鋼筋未發生屈服。屈服彎矩與計算彎矩的最小比值1.34，說明在不考慮計算與實際模擬誤差下，強度還有一定的安全儲備，可以滿足“大震不倒”的抗震要求。塑性區的容許轉角與實際最大轉角的最小比值1.05，順橋向變形滿足要求。

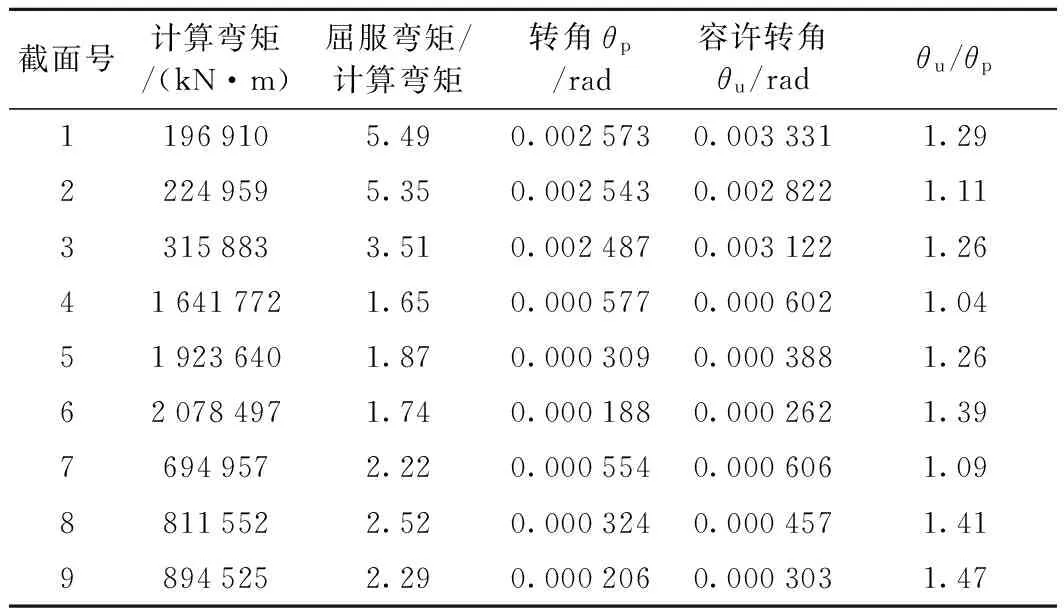
表4 橫橋向截面彎矩與轉角

由表4看出，1～3號截面在橫橋向的計算彎矩還未超過開裂彎矩，處于彈性狀態；6～9號截面橫橋向的計算彎矩雖然超過開裂彎矩但未達到屈服彎矩，橫橋向結構的強度也不存在問題，也完全能滿足“大震不倒”的抗震要求。塑性區的容許轉角與實際最大轉角的最小比值1.04，橫橋向變形也滿足要求。

由表3可知，1號、6號和9號截面屬于控制截面，圖7～圖9給出了地震下3個截面的彎矩曲率曲線即滯回曲線。

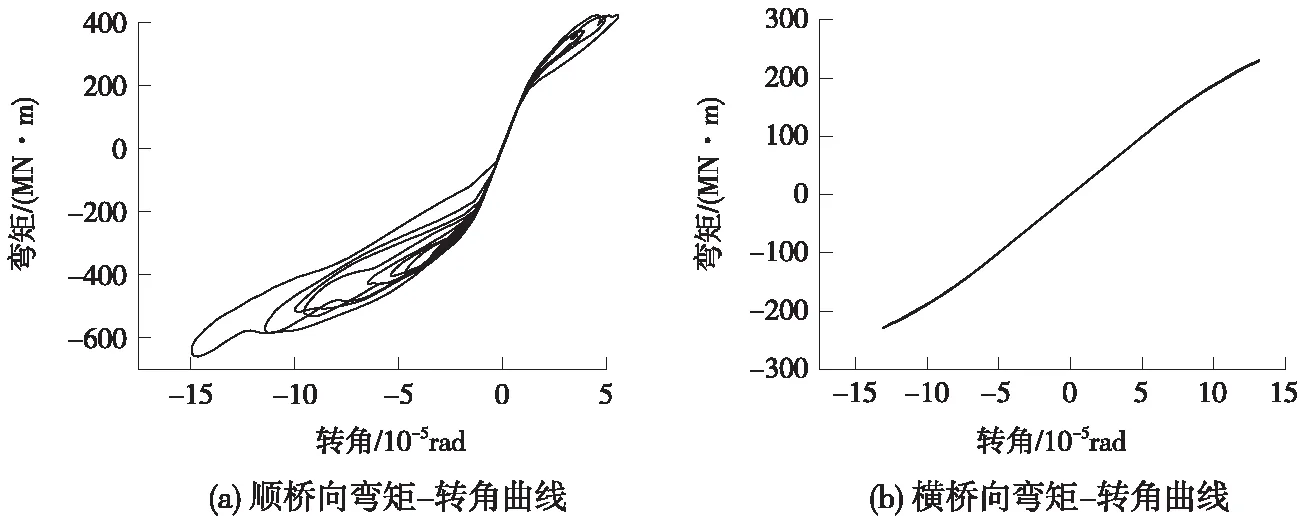
圖7 主墩墩頂截面(1號截面)滯回曲線

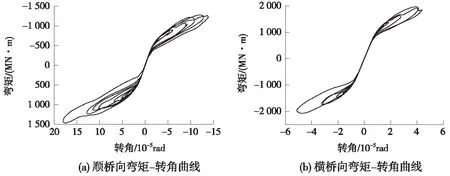
圖8 主墩墩底截面(6號截面)滯回曲線

圖9 次主墩墩底截面(9號截面)滯回曲線

結構處于彈性狀態時，力解除后位移可以歸零，力-位移曲線為一條直線(線彈性狀態)或曲線(非線性彈性狀態)；結構進入塑性后，力解除后存在殘余變形，力-位移曲線為包絡線形狀，并且曲線包絡的面積越大，塑性發展程度越大，結構吸收外部的能量越多[12]。對比圖7～圖9發現，順橋向主墩墩底截面的滯回曲線所包圍的面積最大，說明截面的塑性發展最大，從表3中的屈服彎矩與計算彎矩的比值可以看出，墩底截面的彎矩更加接近理想屈服彎矩，即截面的塑性程度更大，這與滯回曲線反應的內容吻合。對于結構橫橋向，主墩墩頂的滯回曲線為一條略呈“S”形的曲線，說明截面處于彈性狀態，主墩墩底滯回曲線包絡的范圍比次主墩的要大，說明主墩墩底的塑性發展要大，這與表4中反映的情況也是一致的。另外，對比上述3個截面的滯回曲線，可以看出順橋向的滯回曲線包絡的范圍明顯比橫橋向的要大，說明橋墩順橋向塑性發展程度要大，也從側面反映了在地震作用下，對于橋墩截面，順橋向的地震力更為控制設計。這是由于結構是剛構連續梁橋，順橋向的地震力主要由2個剛構主墩來承擔，而橫橋向的地震力主要由主墩及次主墩4個橋墩來承擔。

6 結語

利用Midas/Civil軟件，對金水溝鐵路特大橋，進行了罕遇地震下基于纖維模型的彈塑性地震響應分析，得到如下結論：在進行橋梁的動力彈塑性有限元抗震分析中，基于纖維模型的桿系有限元法較基于集中鉸模型的桿系有限元法具有一定的優勢；對于具有異形截面橋墩的橋梁結構，建立纖維模型時，推薦混凝土與鋼筋分別采用Mander本構關系和修正梅內戈托與平托本構關系；對于剛構連續梁橋，公路抗震規范對于變形的規定比鐵路規范要合理；分析結果表明，主橋結構強度與變形均滿足規范要求，滿足“大震不倒”的抗震設防要求；在橫橋向，連續梁與剛構墩的墩底為控制截面，在順橋向，連續梁墩墩底、剛構墩的墩頂與墩底均為控制截面，塑性發展程度大，需加強抗震構造措施，并且對于這種剛構連續梁橋，順橋向比橫橋向的地震力更加控制設計；通過Midas/Civil軟件直接求出纖維截面的理想彈塑性軸力-彎矩-曲率曲線，其與截面滯回曲線反映的截面抗震性能吻合，因此可用其對截面的抗震性能做出初步評價。

[1] 柳春光.橋梁結構地震響應與抗震性能分析[M].北京：中國建筑工業出版社，2009．

[2] 秦從律，張愛暉.基于截面纖維模型的彈塑性時程分析方法[J].浙江大學學報：工學版，2005，39(7)：1003-1008．

[3] 中華人民共和國住房和城鄉建設部.GB 50111—2006 鐵路工程抗震設計規范[S].北京：中國建筑工業出版社，2006．

[4] 中華人民共和國交通運輸部.JTG/T B02—01—2008 公路橋梁抗震設計細則[S] .北京：人民交通出版社，2008.

[5] 徐庶，蔣新山.應用ANSYS研究受約束鋼筋混凝土承載力性能[J].工程施工技術，2008(4)：92-94.

[6] 禚一,王菲.E2地震作用下減隔振橋梁的抗震設計[J].鐵道標準設計，2013(1)：52-56.

[7] 邁達斯技術有限公司.Midas Civil 2010分析設計原理[M].北京：邁達斯技術有限公司，2010.

[8] 胥開軍.基于纖維模型的鋼筋混凝土柱彈塑性數值模擬[J].四川建筑，2010(2)：106-107.

[9] 邱順冬.橋梁工程軟件Midas Civil常見問題解答[M].北京：人民交通出版社，2009.

[10] 中華人民共和國鐵道部.TB 10002.5—2005 鐵路橋涵地基和基礎設計規范[S].北京：中國鐵道出版社，2009.

[11] 劉俊.長聯多跨剛構-連續梁橋的抗震設計[J].鐵道標準設計，2012(7)：74-81.

[12] 范立礎，卓衛東.橋梁延性抗震設計方法[M].北京：人民交通出版社，2001.

Elastic-plastic Seismic Analysis of Extra-long Jinshuigou Bridge

YUE Ying-jiu

(Bridge & Tunnel Design Department， China Railway First Survey and Design Institute Group Co.，Ltd.，Xi’an， 710043)

In order to understand the respond characteristics of pre-stressed large-span concrete bridge with continuous rigid frame girder and high piers， structural fiber model is established with the application of Midas/Civil software， and Mander constitutive relation and modified Menegotto & Pinto constitutive relation for concrete and reinforcement respectively， to conduct elastic-plastic seismic analysis of the extra-long Jinshuigou Bridge. Results of the analysis show that such micro model can be effectively analog structural seismic reaction and the strength and deformation of the structure under rare earthquake meet the specifications with certain safety reservation. The bottom of pier is dangerous in transverse direction. The top and bottom of the rigid pier and the bottom of the continuous beam pier are all dangerous in longitudinal direction. The earthquake force in longitudinal direction more controls the design of the structure.

Rigid frame continuous bridge; Fiber Model; Rare Earthquake; Elastic-plastic seismic analysis; Constitutive model

2013-12-30；

：2014-01-13

岳迎九(1969—)，男，高級工程師，1990年畢業于西南交通

大學橋梁工程專業，工學學士，E-mail：954910260@qq.com。

1004-2954(2014)09-0079-06

U442.5+5

：A

10.13238/j.issn.1004-2954.2014.09.020