基于單相交錯式并聯PFC的Saber仿真應用研究

范立榮，孫豐濤，李 輝

（珠海格力電器股份有限公司，廣東 珠海519070）

0 引 言

隨著電力電子技術的發展，電力電子技術裝置在工業、農業、國防、科技等領域都得到了廣泛的應用，但電力電子技術裝置本身屬于非線性設備，這些非線性設備的大量使用給用電設備帶來的公共諧波污染不可忽視，并在一定程度上影響了電網供電質量和用戶的使用安全。因此，功率因數校正是目前比較流行的一個專業術語，它的作用不僅僅是提高線路或系統的功率因數，更重要的是可以解決電磁干擾（EMI）和電磁兼容（EMC）問題［1］。

PFC分為有源PFC和無源PFC兩大類，無源PFC雖然結構簡單，成本低，但是輸出直流DC電壓紋波大，質量較差，功率因數也不能做的很高［2］，因此電流諧波成分并不能完全達到國家對諧波的要求，因此目前較流行的是有源PFC技術。

傳統的Boost APFC雖然在1～3 k W的功率范圍可以達到最佳的設計效果，但由于EMI濾波器和電感體積較大，使得它應用在3 k W以上的電路優化設計中會變得很困難，而且它不能適應全負載范圍高效的要求。面對這些挑戰，交錯式PFC能很好地解決這些難題。

Saber軟件是美國Synopsys公司開發的一款EDA軟件，它為復雜的混合信號設計與驗證提供了一個功能強大的混合仿真器，可以解決從系統開發到詳細設計、驗證等一系列問題［3］。本文充分利用Saber的數模混合仿真功能（可以兼容模擬、數字、控制量的混合仿真）對6 k W兩路交錯并聯CCM Boost PFC進行了仿真應用研究。

1 交錯式PFC原理

本文使用Boost PFC變換器拓撲結構為主電路的有源PFC電路，實際應用中交錯PFC控制芯片可采用安森美的NCP1631或TI的UCC28070。圖1給出交錯并聯PFC拓撲原理圖。

圖1 交錯并聯Boost PFC拓撲結構圖

交錯式PFC控制是將工作頻率相同的多個開關功率變換器單元交錯連接的控制策略。在每個開關周期內，每個開關功率變換器單元都只工作相同的時間，但是工作的時間和順序在這個開關周期內呈現有規律的交錯狀態［4］。這種控制策略能在不增加功率開關器件和損耗的前提下，有效降低系統功率總線電流紋波的幅值，提高了功率總線電流紋波的頻率，因此也可以簡化輸入EMI濾波器的設計。

2 基于Saber的交錯式PFC電路仿真

2.1 參數計算

本文設計參數規格如下：

輸入電壓：Uin＝172～270 V，額定電壓為220 V（考慮電網電壓±20%波動），PFC輸出電壓Upfc＝410 V，電網頻率為50 Hz，最大輸出功率Pout＝6 000 W，PFC效率η＝0.90，開關頻率fs＝200～300 k Hz，這樣可以使功率級主電路小型化，為了減小失真，保持高效率，這里采用200 k Hz。

電感的大小決定了輸入端紋波電流的總量。因此可按照給出的紋波電流值來計算電感值。設最大峰值電流Ipk為

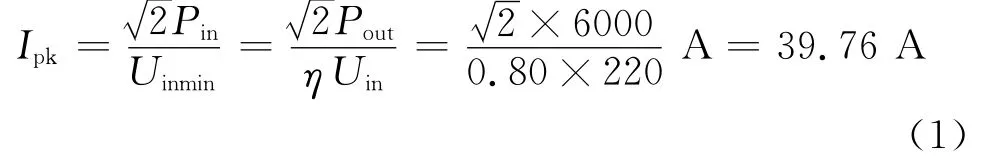
電感中的紋波電流通常選擇在最大峰值電流的20%左右，電感值根據輸入電壓和開關頻率的占空比來選擇，占空比D的計算公式為：

則最小電感值公式為：

取L1＝L2＝400μH，式（3）中fs為開關頻率，ΔI為紋波電流峰峰值。

通常選擇大電解電容作為輸出電容，和輸出電容選擇相關的參數有開關頻率fs，紋波電流峰峰值ΔI，直流輸出電壓Uo，輸出紋波電壓ΔU和維持時間Δt。維持時間是指在輸入電源被關閉后，輸出電壓仍然保持在規定范圍內的時間，通常取15～50 ms，這里可以取為15 ms，則電容值為：

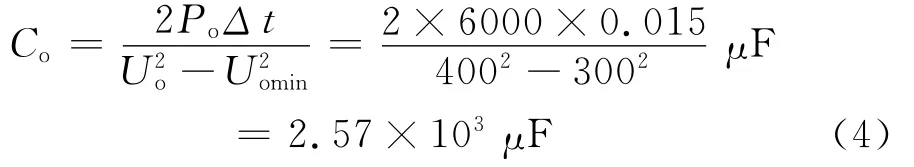
仿真取2 820μF。

開關管是速電壓型，其反向恢復時間為200 ns，擊穿電壓為600 V，正向電流有效值為50 A，選用IXFN64 N60P。

2.2 系統原理圖

如圖2所示，系統由2個電流內環和一個電壓外環構成，開關管暫用Saber中理想開關管sw1＿l4＿1代替，每個Boost電感都工作在恒頻、恒調節占空比的模式，能夠自動實現輸入的功率因數校正。在一個開關周期內，開關管Q1的驅動信號滯后開關管Q2的驅動信號半個周期。因此，總線上的電流為每個單元電感電流之和。在相同輸出功率條件下，紋波的幅值會減小，且紋波的頻率增加為開關頻率的二倍，因此能大大減小輸入濾波器的體積和每個開關管上的電流應力，特別適用于大電流、低電壓場合。

2.3 系統仿真

2.3.1 直流分析

DC分析旨在為系統找到電路的工作點，即為系統提供一個靜態工作點，圖3給出進行DC分析的部分結果。

2.3.2 瞬態分析

利用Saber軟件對圖2電路進行瞬態仿真分析（進行瞬態分析之前必須先進行DC分析），Saber的數模混合仿真要注意模擬量與數字量之間的轉換，模擬量是有量綱的，而數字量是無量綱的，因此在轉換成數字量時必須通過v2var（電壓變換成數字）或i2var（電流變換成數字），反之同理，同時設置好電壓外環與電流內環的PI及抗飽和積分限幅數。圖4上方粗實線即為PFC輸出電壓采樣波形，從圖4可以看出，PFC采樣電壓穩定在2.5 V上下（偏差0.15 V），說明輸出電壓基本穩定；圖4下方波形即為整流輸出采樣電壓波形。

圖5為輸入電壓采樣與2電感支路電流波形，此波形是從交流全波整流后采樣得到的正弦半波。此波形通過相關運算進入電流測定比較器，控制電感電流使之跟蹤交流輸入電流。從圖5可看出，2支路電感電流均能很好跟蹤交流輸入電流，從而達到控制功率因數的目的。

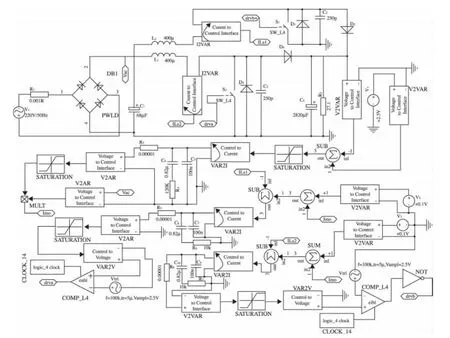
圖2 交錯并聯Boost PFC Saber仿真原理圖

圖3 DC分析部分結果

圖4 PFC輸出與整流輸出采樣電壓波形

圖6 為驅動上下開關管的驅動電壓與2支路電感電流波形，從圖6可以看出，DRVA與DRVB兩路移相180°驅動信號，最小占空比為0.4488，2支路電感紋波分別為3.2503 A和3.2102 A，相差0.04 A左右，可見2路電感取值相同時對各個支路紋波影響較小。

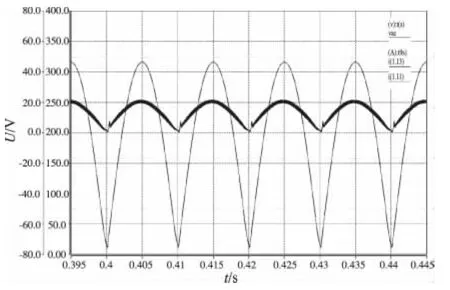
圖5 交流輸入電壓與2電感支路電流采樣波形

圖6 2路驅動信號與2路電感支路電壓波形

圖7 （a）為輸入總電流與2支路電感電流波形，圖7（b）為其展開波形，從7（b）放大后可以看出，2電感支路紋波電流分別為2.279 3 A與2.282 6 A，而總電流紋波電流為1.4484 A，即通過交錯式PFC控制，能使2支路電感紋波電流相互抵消，從而使總電流紋波下降。

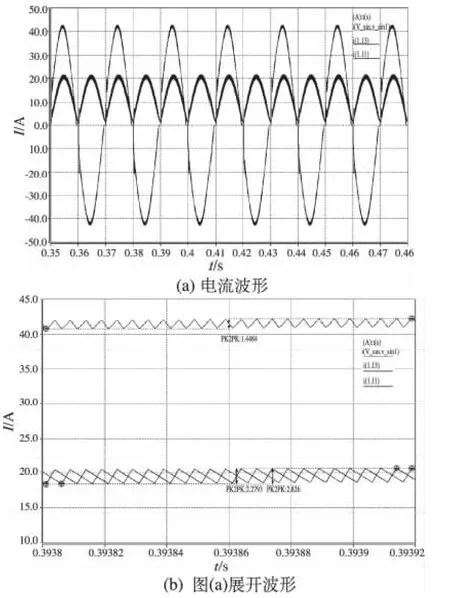
圖7 輸入電流與2電感支路電流波形

圖8 為輸入電壓與輸入電流波形，從中可以看出，輸入電流波形與輸入電壓波形反相，輸入電流波形能很好地跟蹤輸入電壓波形，電流畸變率已經很小（僅在開關關斷時有毛刺），因此驗證了交錯式PFC在中大功率（超過3 k W）上應用的優越性。

2.3.3 參數掃描分析

以上仿真是建立在2路電感參數完全一致的情況下，但實際中由于材料及加工工藝的不同，2路電感不可能完全相同。因此為考慮2路電感有偏差的時候對其支路及其輸入電流紋波的影響，對L1或L2任一進行參數掃描分析，如圖9是其設置框圖。對L1進行參數掃描，考慮±10%的誤差，對L1取值從360μH到440 μH進行掃描，每次步進40μH，即分別對L1＝360 μH、400μH和440μH進行3次瞬態分析，觀察2路電感取值存在一定誤差時對其支路電流和輸入電流紋波的影響，圖10是取L1＝440μH即影響比較明顯的波形。

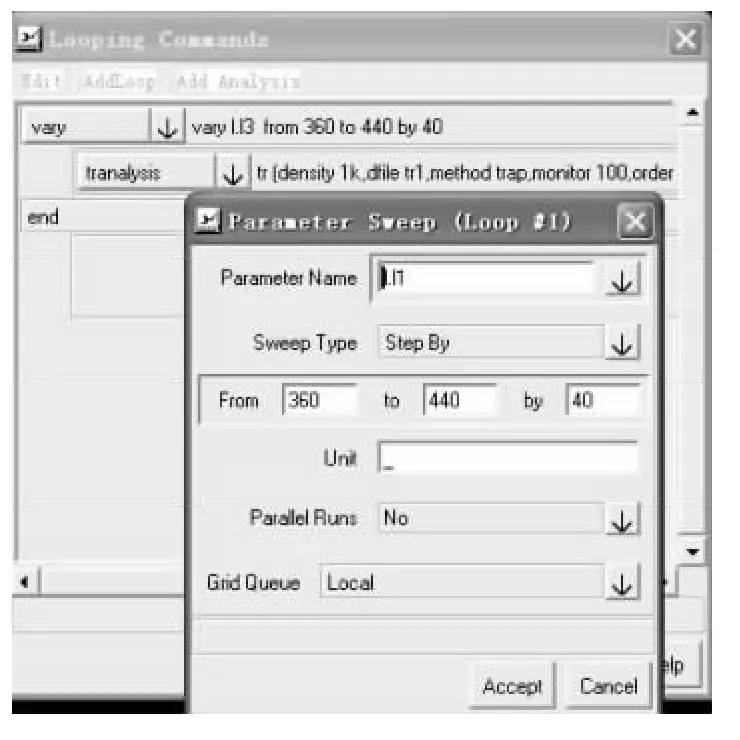
圖9 對電感L 1進行參數掃描設置

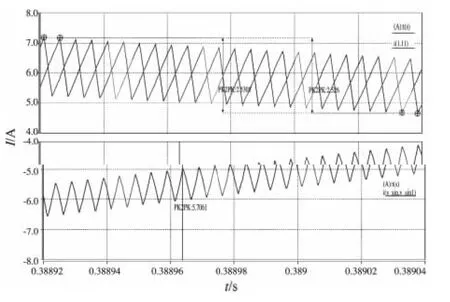
圖10 取L 1＝440μH時2支路電感電流與輸入電流局部波形

從圖10可以看出，2電感支路紋波電流分別為2.5305 A與2.526 A，較之前的2.2793 A與2.2826 A明顯增大，且總輸入電流紋波變為5.7061 A，較電感支路相同的1.4484 A增加顯著，因此交錯式PFC控制2電感支路電感必須上下對稱（即電感取值誤差不能超過±10%，應在盡量小的范圍）。仿真發現，2支路電感若在±5%范圍內對其輸入電流紋波影響不大。

2.3.4 FFT分析

利用Saber仿真軟件可以方便地對其進行FFT分析，在瞬態分析取得足夠長的周期（保證FFT分析時數據采樣的準確）時，可進行FFT分析，觀察輸入電流的TDH及各次諧波電流的幅值是否滿足要求，圖11是其FFT分析波形。

從圖11可以看出，基波幅值為42.719 A，其余各次諧波均為基次諧波（2 N－1，N從1開始），無偶次諧波，利用Saber的圖形觀測器測得其前30次諧波幅值如表1所示。

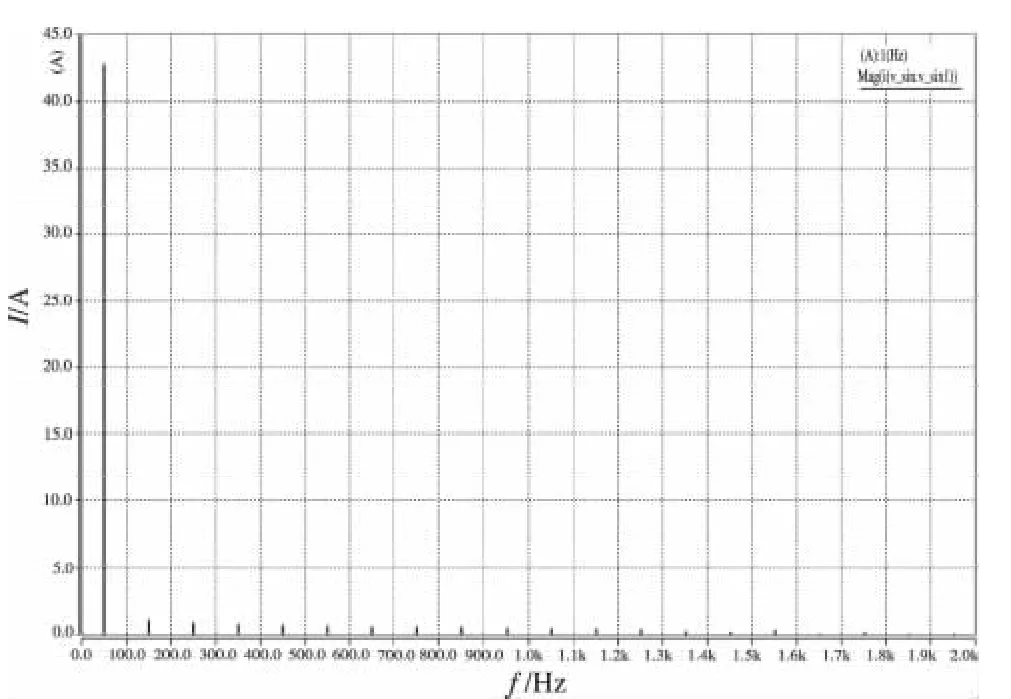
圖11 FFT分析波形

從表1可以看出，前20次諧波幅值均在0.50 A以上，20次以后均小于0.50 A，因此主要濾除20次以內的基次諧波，而20次以內又主要以濾除3、5、7、9、11、13次，因此計算前20次諧波畸變率為：

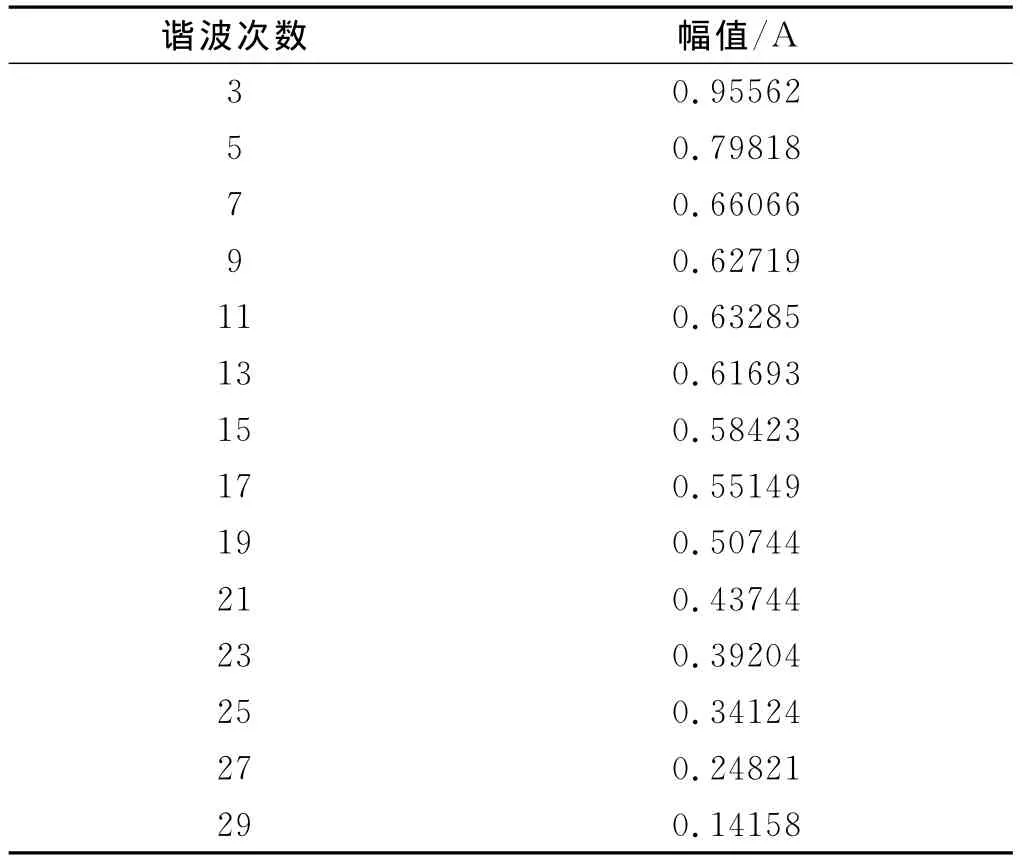
表1 FFT分析各次諧波幅值

即THD＝4.7%，小于GB（＜5%）要求，因此設計滿足要求。同時為進一步減小諧波，可以在電源輸入側加裝濾波器進行濾除。關于前面EMC濾波器設計，因本文主要研究交錯式PFC設計，故這里不再介紹。

3 結束語

本文主要借助Synosys公司強大的數模混合仿真軟件對單相交錯并聯式PFC電路進行了深入的仿真應用研究，在分析單相交錯式PFC原理的基礎上利用Saber仿真軟件對6 k W兩路交錯式PFC先是進行了詳細的設計和參數計算，之后通過Saber仿真，使設計達到了要求。同時仿真結果不僅驗證了交錯并聯式PFC原理的正確性，而且對于縮短開發周期，降低設計成本及軟件的工程調試也有一定的指導意義。

［1］ 楊潮暉.Boost－PFC電路拓撲和數字控制的研究［D］.哈爾濱：哈爾濱工業大學碩士學位論文，2010.

［2］ 魯 曄，郭穎娜，程為彬.基于Saber的Boost APFC電路設計與仿真［J］.模擬應用，2009，02：21－23.

［3］ 朱娟娟.基于Saber的單相Boost電路仿真與設計［J］.科技廣場，2007，11：213－215.

［4］ 劉 晟.有源功率因數校正的新型控制策略研究［D］.南京：河海大學碩士學位論文，2007.