弧齒錐齒輪參數化設計
邵立新
(河南職業技術學院,河南 鄭州 450000)
弧齒錐齒輪是能夠完成相交軸之間傳動的一種新型齒輪,由于該種齒輪在兼顧加工工藝性的基礎上選擇準線,不僅形成的齒廓面為便于加工的規律曲面,而且仍具有一般錐齒輪的優良傳動性,目前已廣泛應用在航空、航天、冶金、礦山機械、起重運輸機械等大型機械中。但圓弧錐齒輪加工的復雜性是當前的難題,而數控加工技術對加工高精度、高難度的零件提供了方便,文章研究對數控加工提供了很好的條件。同時也為以后進一步進行齒輪噪聲控制和優化設計奠定基礎,從而提高產品設計效率和精度,縮短新產品開發周期,這有著非常廣泛的應用前景和十分重要的社會效益和經濟效益。
1 弧齒錐齒輪的參數化建模
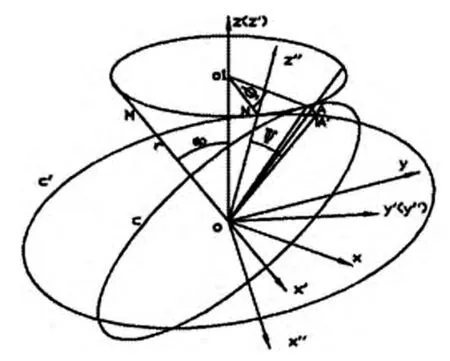
圖1 球面漸開線形成方式
錐齒輪的齒廓理論上為復雜的空間曲線,即球面漸開線。弧齒錐齒輪的理想齒面是由一簇相似的球面漸開線組成,由于齒廓曲線不是平面曲線,并且輪齒沿著齒寬方向也是變化的,球面無法展開成平面,所以圓錐齒輪的設計和制造一般都采用與球面漸開線非常接近的錐面漸開線代替球面漸開線,影響設計精度。由球面漸開線的形成原理和基本特性入手推導球面漸開線方程和與弧齒錐齒輪幾何尺寸相關的計算公式,利用UG的表達式功能,
建立相應表達式生成球面漸開線曲線及其他相互關聯的曲線。并通過特征操作實現弧齒錐齒輪的參數化設計,精準地建立弧齒錐齒輪的三維模型。
根據設計需要,更改相應參數,就可以更新三維模型,從而提高設計效率,為弧齒錐齒輪的嚙合仿真分析、有限元分析打下基礎。
2 球面漸開線的數學模型
弧齒錐齒輪的傳動原理是由兩個圓錐體的摩擦機構來體現的。就單一的弧齒錐齒輪而言,其運動就是基圓錐相對于平面進行的純滾動。但是,以一對相互嚙合的弧齒錐齒輪而言,其運動即為空間球面運動。因此,對于兩個相互嚙合的弧齒錐齒輪,只有與弧齒錐齒輪頂點等距離的各對應點才互相嚙合,即弧齒錐齒輪齒廓應為球面漸開線。這是弧齒錐齒輪副嚙合的基本特點。如圖1所示,圓平面C(圓心為O,半徑為外錐距R,與基錐M相切的平面)與基錐角為的基錐M相切于OA,當C沿M按一個方向滾動時(圖中為順時針方向),平面C上的任一徑向直線將在空間畫出球面漸開線的錐面,圓平面C的圓周點A滾動生成的曲線就是球面漸開線。
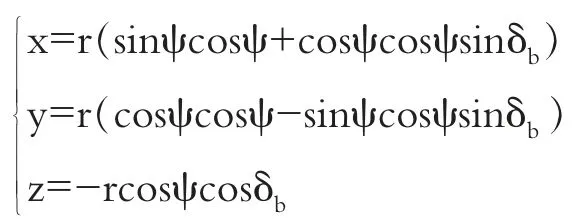
式1中,r為錐齒輪的外錐距即球面半徑;為基錐角;φ 為嚙合面上起始線段與瞬時回轉軸之間的夾角,在基圓錐上φ 為零。
3 弧齒錐齒輪的創建
計算弧齒錐齒輪的基本參數,通過球面漸開線方程和分錐面螺旋線方程,建立弧齒錐齒輪的各個參數之間的方程,利用UG表達式方式進行參數化建模。主要步驟如下:

圖2 主動輪模型
(1)新建模型文件,在表達式界面中輸入齒輪的基本參數,然后輸入兩端面的球面參數方程和分錐面螺旋線以及各個參數間的關系式并保存。
(2)創建直徑相對應的齒根圓、分度圓和齒頂圓。
(3)由規律曲線功能,創建漸開線以及分度圓錐螺旋線,修剪曲線得到齒廓曲線。
(4)將齒廓曲線掃掠成單齒。
(5)根據齒輪的參數運用“回轉”功能,生成齒坯。
(6)把生成的單齒實體繞z軸旋轉,角度為360/z度,選擇副本數為z-1即可生成要求的齒輪實體,如圖2所示。
(7)根據以上參數化建模過程,把該弧齒錐齒的表達式導出,新建模型后導入已經導出的表達式,修改對應的齒輪參數值,按照同樣的方法,即可建立與之相嚙合的從動弧齒錐齒輪的三維實體模型。
文章以三維設計軟件UG為平臺,在研究弧齒錐齒輪的數學模型的基礎上,實現了弧齒錐齒輪的三維造型。從而保證弧齒錐齒輪造型的精確性和快速性,為后續工作奠定了基礎。對所生成的弧齒錐齒輪進行運動仿真分析,不僅驗證了設計的合理性,而且可導出視頻文件直觀的了解其運動原理。最后對所生成的弧齒錐齒輪進行有限元模態分析,得到弧齒錐齒輪的低階固有振動頻率和主振型,反映了弧齒錐齒輪的動力學性能,利用分析結果還可直觀的分析齒輪的動態特性、發現薄弱環節,為齒輪的動態性能實驗、設計、維護提供理論依據的同時也為系統的動態響應計算和分析打下基礎。
[1]陳霞.直齒錐齒輪修形方法研究[D].武漢:華中科技大學,2008.
[2]谷鳳民,周亮,段建中,等.弧齒錐齒輪的一種新型精確設計方法[J].機械設計與制造, 2008,(12): 12-13.
[3]數字化手冊編委會.機械設計手冊(新編軟件版)[D].北京:化學工業出版社,2008.
[4]何雪明,吳曉光,王宗才.機械CAD/CAM 基礎[M].武漢:華中科技大學出版,2008.

