雙Y移30°PMSM兩電機串聯系統的諧波效應

劉陵順， 張少一， 劉華菘

(海軍航空工程學院控制工程系，山東煙臺 264001)

0 引言

全電艦船、多電飛機概念的提出，以及機車牽引、機器人、紡織、造紙等工業用電系統的應用要求，需要研究解耦運行的多電機交流傳動系統，為此提出了一種基于廣義零序諧波分量的單逆變器驅動雙Y移30°PMSM兩電機串聯系統。該系統是由兩臺雙Y移30°PMSM按照一定的定子繞組聯結規則串聯而成，可在同一逆變器和同一套控制平臺下實現各臺電機的解耦運行，有助于節省控制驅動裝置及其外圍電路，降低了系統的體積、重量與成本。目前對于單逆變器驅動多電機串聯系統的研究多以原理可行性探索為主，研究對象主要集中在多相感應電動機串聯系統，對于多相PMSM串聯系統的研究還較為少見［1］，已有文獻主要研究了理想正弦波磁場分布下多電機串聯系統的基本原理和控制策略［2－5］。由于電機的實際氣隙磁場通常存在著一系列的高次諧波，將對串聯系統的解耦控制產生影響。為此，文獻［6］采用虛擬多電機機電耦合的概念就五相PMSM反電動勢諧波對串聯系統矢量控制的影響進行了分析，文獻［7］分別研究了2臺五相電機串聯系統以及對稱六相串聯三相電機系統的定子繞組設計特點。考慮到雙Y移電機可靠性更強，其力矩脈動平均值只有對稱六相電機的14%，諧波電流較小，雙Y移30°PMSM兩電機串聯系統具有更大的軍事應用價值。本文以定子集中繞組的雙Y移30°PMSM為研究對象，利用繞組函數的概念，研究了不同類別的高次空間諧波與另一臺相串聯的雙Y移30°PMSM基波磁動勢相互作用對系統解耦運行產生的影響規律，建立了該串聯系統中其中一臺PMSM包含5、7次空間諧波的多維空間數學模型，進行了變速、變負載的仿真研究，揭示了該串聯系統多相PMSM定子繞組必須為正弦波分布的根本原因。

1 高次空間諧波的耦合效應分析

正弦波分布的雙Y移30°PMSM基于自然坐標系下的數學模型經過全維空間解耦矩陣運算后，變換到由dq－xy－o1o23個正交基組成的正交平面上，其中電機的電磁轉矩完全是由dq電流分量決定，而與它們的xy電流分量和o1o2零序分量無關［8－12］。因此，雙Y移30°PMSM的磁通和轉矩控制只需要dq平面上的兩個電流分量即可，而xy平面的2個電流分量可以用來控制另一臺雙Y移30°PMSM，為此需將另一臺電機的定子繞組與第一臺電機的定子繞組通過適當的相序轉換串聯在一起，保證第一臺電機的磁通和轉矩生成電流分量不會在在第二臺電機中生成磁通和轉矩，反之亦然。2臺雙Y移30°PMSM串聯系統與逆變器的聯結圖如圖1所示。

為了分析圖1串聯PMSM定子繞組必須為正弦分布，下面利用PMSM1含有所有諧波的集中繞組研究各類諧波對解耦運行的影響情況，假設定子繞組分布不對稱，則PMSM1中的高次諧波主要有:12i±1次(i=1，2，3，…)以及6i±1次(i=1，3，5，…)兩大類奇次諧波以及各偶次諧波。

圖1 兩臺雙Y移30°PMSM串聯系統Fig.1 Dual Y shift 30°PMSM series-connected system

根據圖1中的聯結關系，假設兩臺電機的基波電流的初始相位為零，則可得逆變器輸出電流與2

臺串聯電機電流的關系為［7］

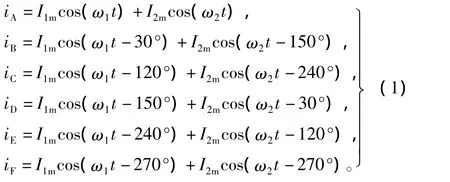
其中，I1m，I2m分別為2臺電機基波電流分量的幅值，ω1，ω2分別為2臺電機基波電流分量的角頻率。

假定PMSM1短距集中繞組下a相的繞組函數如圖2所示。

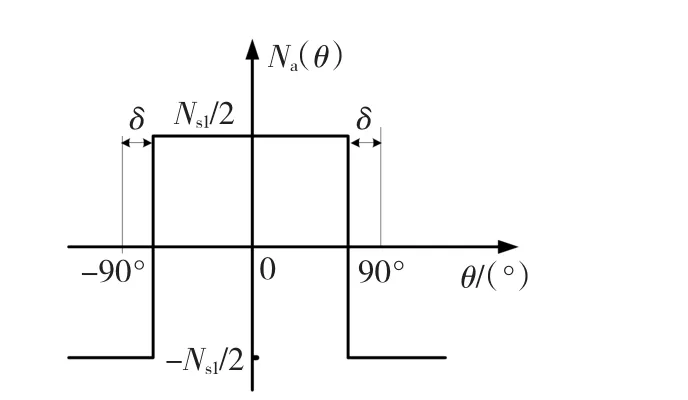
圖2 短距集中繞組下a相的繞組函數波形Fig.2 Winding function waveform of short-pitched concentrated coil

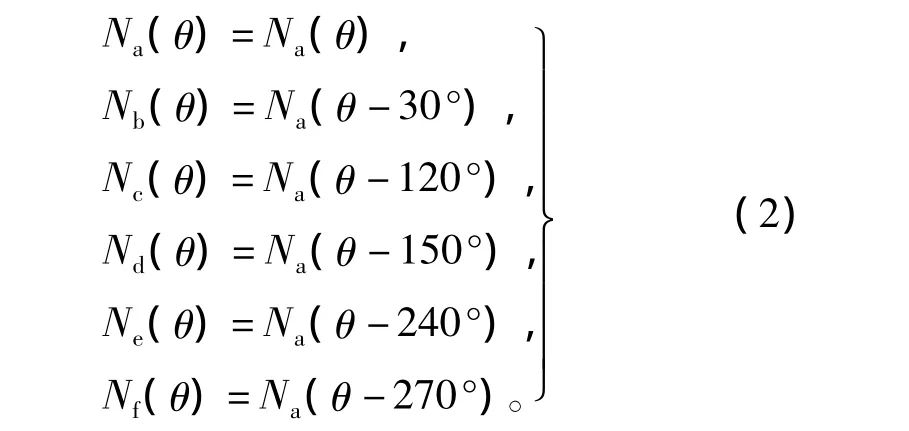
設PMSM1每相繞組的總有效匝數為Ns1，δ為短距角度，各相繞組函數之間的關系為

所以PMSM1定子繞組的傅里葉函數推導為

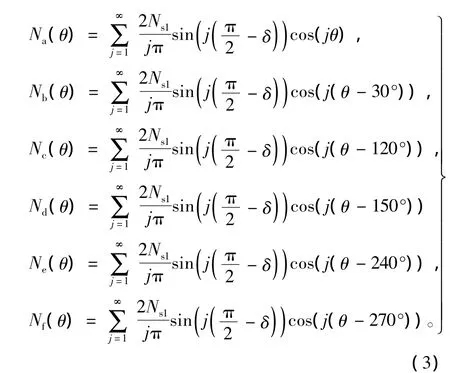
利用式(1)中PMSM2的磁通、轉矩基波電流以及式(3)，可得PMSM1中的第j次諧波與PMSM2基波電流產生的磁動勢表達式為

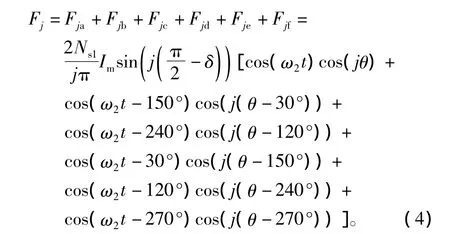
據此可以推導出PMSM1氣隙磁場中各類諧波與PMSM2的耦合作用，具體討論如下:

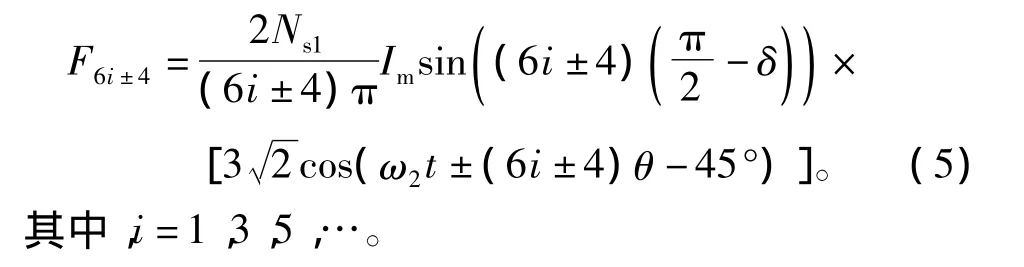
據此，PMSM1的(6i±4)次諧波(i=1，3，5，…)與PMSM2的基波電流耦合在PMSM1內產生旋轉磁場。(6i+4)次諧波產生的旋轉磁場轉向與PMSM2的基波磁場相反，(6i－4)次諧波產生的旋轉磁場轉向與PMSM2的基波磁場相同。

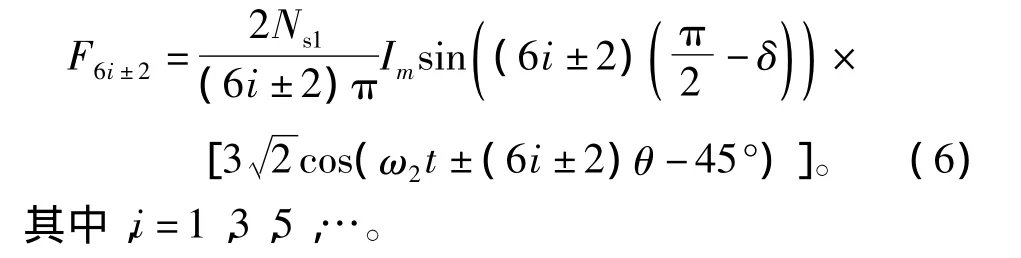
據此，PMSM1的(6i±2)次諧波(i=1，3，5，…)，與PMSM2的基波電流耦合在PMSM1內產生旋轉磁場。(6i+2)次諧波產生的旋轉磁場轉向與PMSM2基波磁場相同。(6i－2)次諧波產生的旋轉磁場轉向與PMSM2基波磁場相反。

同理，對于PMSM1中的奇次諧波與PMSM2的

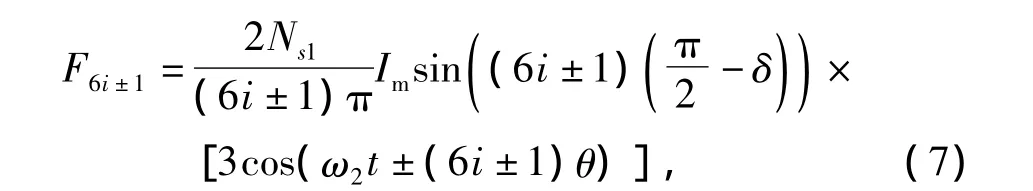
其中，i=1，3，5，…。

(6i±1)次諧波(i=1，3，5，…)與PMSM2的基波電流耦合在PMSM1內產生旋轉磁場。其中(6i+1)次諧波產生的旋轉磁場轉向與PMSM2的基波磁場相反，(6i－1)次諧波產生的旋轉磁場轉向與PMSM2基波磁場相同。

此外，(12i±1)次奇次諧波(1，11，13，23，25…)以及3的倍數次諧波，將不會與PMSM2的基波電流產生耦合，因而，其產生的旋轉磁動勢為零。

由此可見，PMSM2的基波電流與PMSM1的某些高次諧波互相耦合，在PMSM1中產生旋轉磁動勢，其旋轉速度由兩臺串聯電機的同步轉速ω1和ω2共同控制，通常情況下 ω2與 ω1不相等，會在PMSM1中產生電磁轉矩脈動，從而影響PMSM1的正常運行。因此，在該串聯系統中，務必要求兩臺串聯電機的磁場分布呈正弦波，且在空間對稱分布，從而消除各偶次諧波以及(6i±1)次奇次諧波，i=1，3，5，…。

另外，盡管PMSM1中的(12i±1)次諧波不與PMSM2的基波電流耦合產生旋轉磁動勢，但它們會與自身的基波電流分量作用產生高次轉矩紋波，因此，在電機設計中需要消除這些諧波。基波電流相互耦合的效果分析如下:

25 、7次空間諧波對解耦控制的影響仿真

2.1 含5、7次諧波的串聯系統數學模型

通常電機的定子繞組呈對稱分布，偶次諧波自然消失。為了驗證串聯電機的(6i±1)奇次諧波(i=1，3，5，…)，對該串聯系統運行存在的耦合問題，假定PMSM1中包含5、7次諧波(其他更高次諧波由于幅值過小可忽略)，PMSM2中氣隙磁場只有基波，不存在高次諧波。

設Ns1Ns1為PMSM1的每相定子繞組匝數，φfm1φfm1為PMSM1永磁主磁通，θr1為PMSM1轉子磁場軸線與定子A相繞組軸線之間的電角度，φfm1－5為PMSM1的5次諧波磁通，φfm1－7為PMSM1的7次諧波磁通，Ns1－5為PMSM1的5次諧波等效繞組匝數，Ns1－7為PMSM1的7次諧波等效繞組匝數，Ns2為PMSM2的定子繞組匝數，φfm2為PMSM2永磁主磁通，θr2為PMSM2轉子磁場軸線與定子A相繞組軸線之間的電角度。

PMSM1的轉子磁場與定子繞組交鏈的磁鏈為

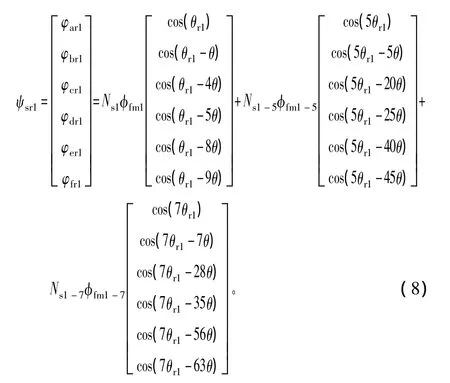
PMSM2轉子磁場交鏈在定子各相繞組中的磁鏈為

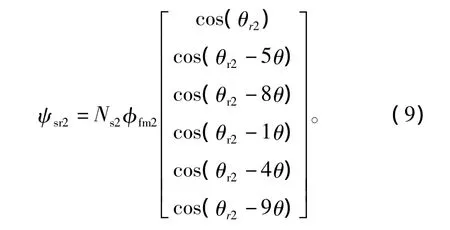
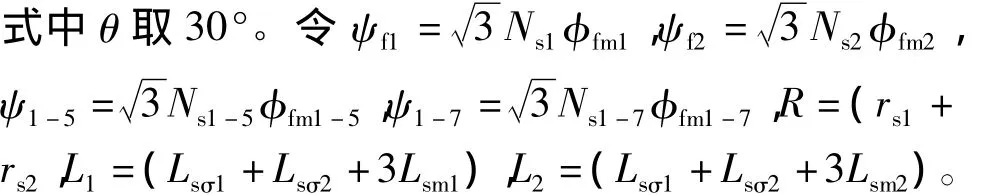
經同步旋轉坐標變換后，可推出PMSM1和PMSM2電壓方程為

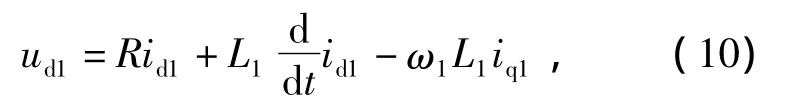
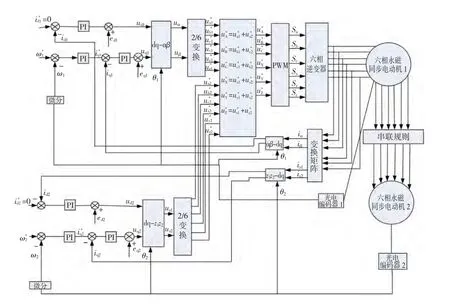
圖3 串聯系統基于id=0的矢量控制系統圖Fig.3 Vector control system based on id=0 for series-connected system

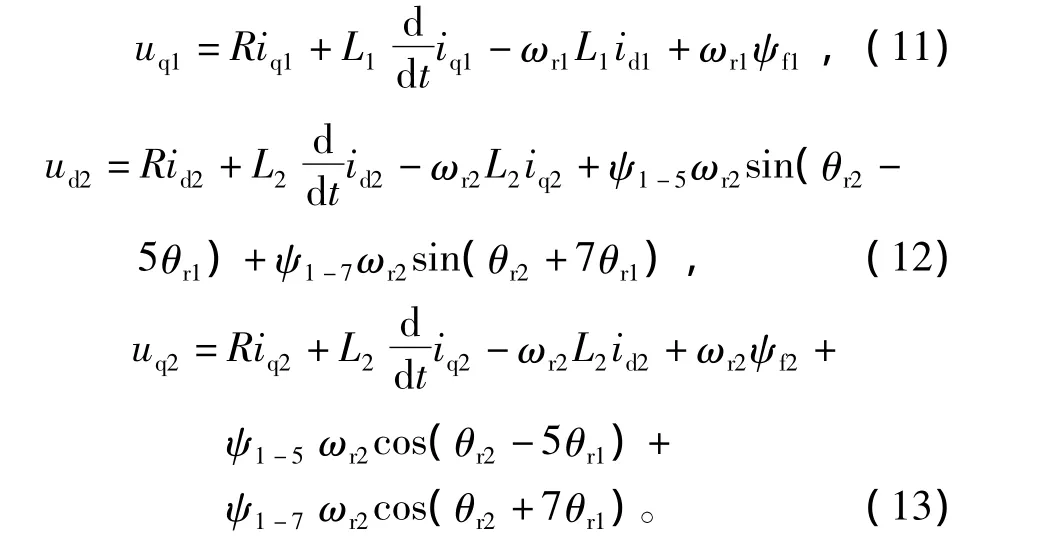
PMSM1和PMSM2的轉矩方程分別為

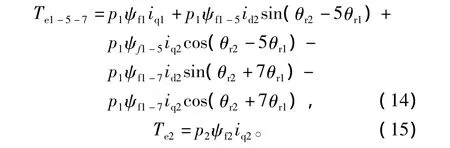
分析式(14)、式(15)可見，在PMSM2的id2或iq2id2非零時，PMSM1的電磁轉矩必有脈動，脈動幅值主要與id2、iq2以及空間諧波 ψ1－5、ψ1－7的大小相關，脈動的頻率和2臺電機的轉速都相關。PMSM2的轉矩只與自身的iq2和ψf2有關，不受PMSM1的空間諧波影響。

2.2 PMSM1含5、7次諧波串聯系統耦合性能仿真

為了驗證PMSM1含有的5、7次空間諧波會影響串聯系統的解耦控制，采用id=0的載波調制

PWM矢量控制策略對2臺雙Y移30°PMSM串聯系統建模仿真，如圖3所示。參數設置:極數p1=p2=4，磁通 ψf1=ψf2=0.2 Wb，ψ1－5=0.08 Wb，ψ1－7=0.06 Wb，摩擦系數B1=B2=0.05，轉動慣量J1=J2=0.1 kg·m2，R1=R2=2.875 Ω，L1=L2=0.12 H。

PMSM1變負載仿真如圖4所示:PMSM1含5、7次空間諧波，初始負載為1 N·m，在1 s從1 N·m增加到10 N·m，轉速為200 r/min;PMSM2不含諧波，負載為2 N·m不變，轉速為250 r/min。

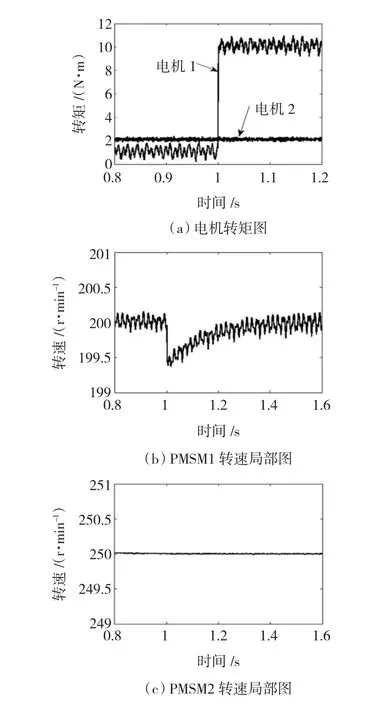
圖4 PMSM1變負載運行Fig.4 Variable load operating of PMSM1

由以上仿真可知:

1)當PMSM1含5、7次空間諧波，PMSM2只有基波時，只要PMSM2帶負載，即iq2存在，PMSM1就存在轉矩和轉速脈動，脈動的頻率和幅值與PMSM1的負載變化無關。

2)PMSM1的負載增加對PMSM2的轉速和轉矩均無影響，這說明不含空間諧波的PMSM2在該串聯系統中不受PMSM1的變載影響。

3)PMSM1的負載在1 s增加時，其轉速小幅下降并迅速恢復。

PMSM2變負載仿真如圖5所示:PMSM1含5、7次空間諧波，空載不變，轉速設為200 r/min;PMSM2不含諧波，負載為2 N·m，在1 s時從2 N·m變為10 N·m，轉速設為250 r/min。

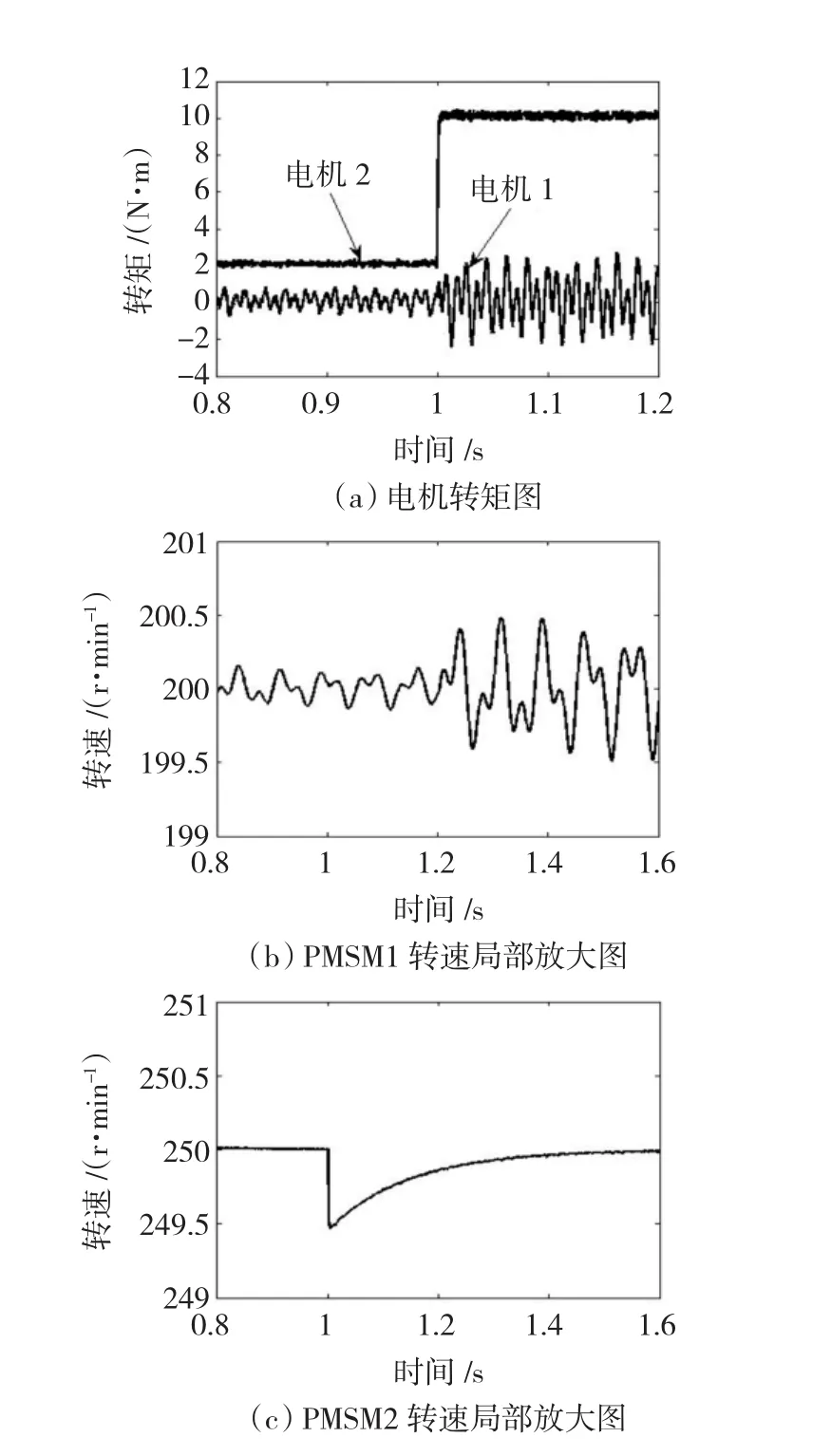
圖5 PMSM2變負載運行Fig.5 Variable load operating of PMSM2

1)PMSM2的負載增大后，PMSM1的轉矩和轉速脈動幅值都增大，即PMSM1的轉矩和轉速脈動幅值受PMSM2的負載影響，脈動頻率與PMSM2的負載大小無關。

2)PMSM2在1s負載增加后轉速小幅下降，并迅速恢復。且不含諧波的PMSM2負載變化時，其自身的轉矩和轉速不存在任何脈動。

PMSM1變速仿真如圖6所示:PMSM1含5、7次空間諧波，且空載運行，初始給定為200 r/min，在0.9 s從200 r/min加速到350 r/min;PMSM2不含諧波，其負載為2 N·m，給定轉速為250 r/min。

1)PMSM1的轉速增加對PMSM2的轉速、轉矩均無影響，這說明不含空間諧波的PMSM2在該串聯系統中不受PMSM1的變速影響。

2)比較PMSM1變速前后的轉速圖，PMSM1的轉速增加使其轉速脈動的頻率有所升高。

PMSM2變速仿真如圖7所示:PMSM1含5、7次空間諧波，且空載運行，給定轉速為200 r/min;PMSM2不含諧波，其負載為2 N·m，在0.9 s從100 r/min加速到400 r/min。

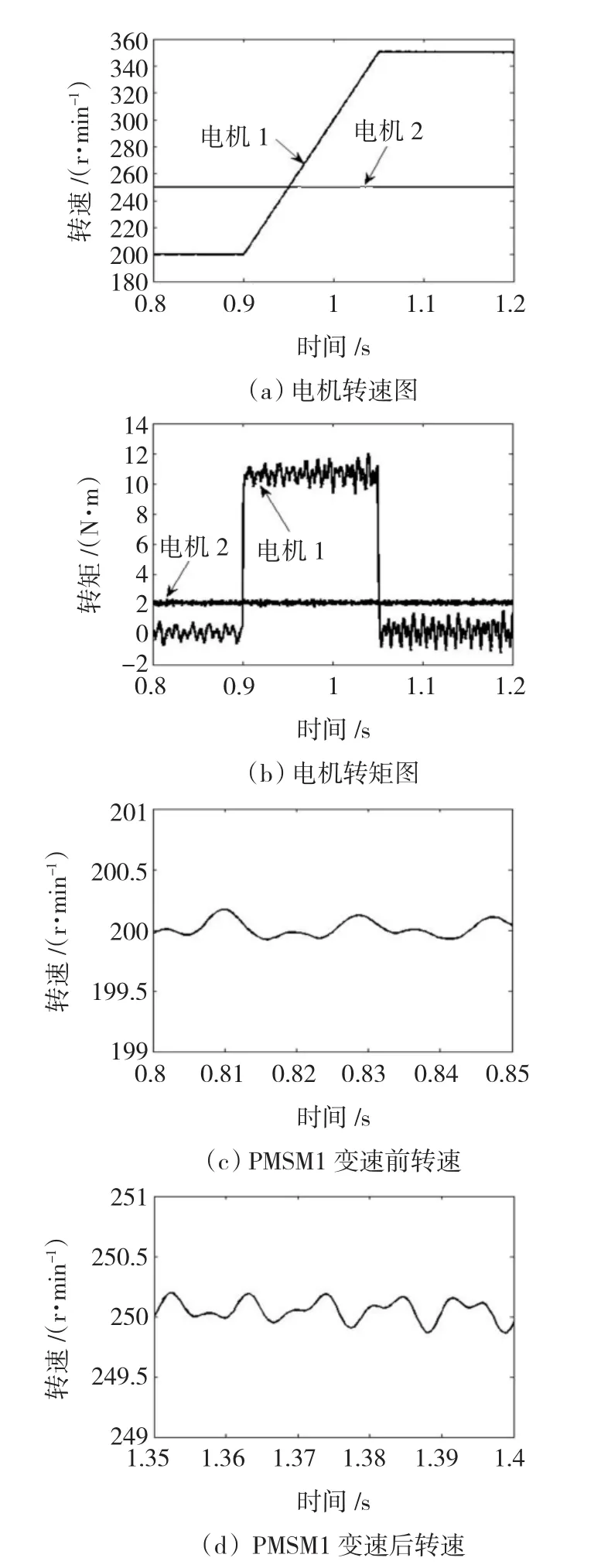
圖6 PMSM1變速運行Fig.6 Variable speed operating of PMSM1

在PMSM2的轉速增加過程中，PMSM1的轉矩脈動幅值和頻率均有所增大。但PMSM2的轉速和轉矩均不存在脈動。

從以上仿真可以得出結論:

1)含5、7次空間諧波的PMSM1轉矩脈動與PMSM2的負載大小有關，脈動頻率與PMSM1以及PMSM2的轉速都相關，因此該串聯系統中PMSM1的運行是不解耦的。

2)若PMSM2不含空間諧波，其運行不受PMSM1變載變速的影響。因此，若實現該串聯系統中2臺電機的解耦運行，每臺電機均不能包含(6i±1)奇次諧波(i=1，3，5，…)。

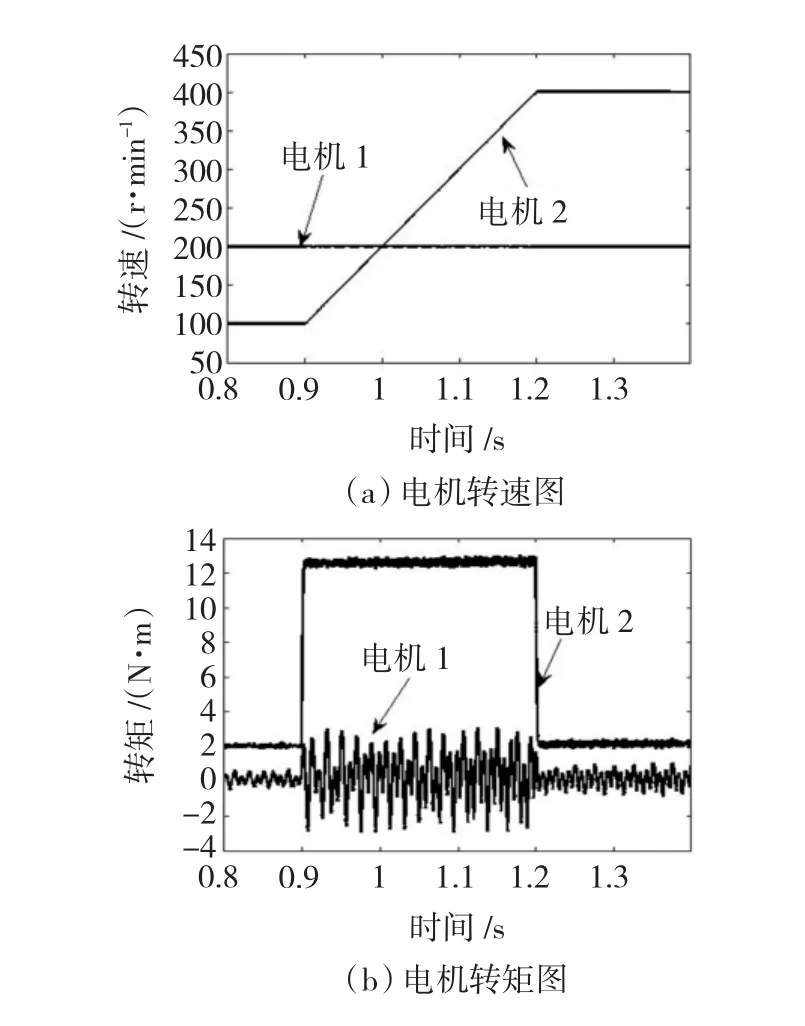
圖7 PMSM2變速運行Fig.7 Variable speed operating of PMSM2

3 結語

為了分析電機高次空間諧波對串聯系統解耦運行的影響規律，本文建立了雙Y移30°六相PMSM集中繞組函數的傅里葉變換式，利用PMSM1高次諧波與PMSM2基波電流耦合的磁動勢關系式，分析了不同類別的高次諧波對串聯系統解耦運行的影響規律，建立了該串聯系統的數學模型并進行了變速、變負載仿真，提出了串聯系統多相PMSM定子繞組必須為正弦波分布的必然要求，為電機的優化設計及空間諧波補償的解耦控制提供理論基礎。

［1］LEVI E.Multiphase electric machines for variable-speed applications［J］.IEEE Transactions on Industrial Electronics，2008，55(5):1893－1909.

［2］LEVI E，JONES M.A novel concept of a multiphase multimotor vector controlled drive system supplied from a single voltage source inverter［J］.IEEE Transactions on Power Electronics，2004，19(2):320－335.

［3］LEVI E，JONES M，VUKOSAVIC S N，et al.Operating principles of a novel multiphase multimotor vector-controlled drive［J］.IEEE Transactions on Energy Conversion，2004，19(3):508－517.

［4］IQBAL A，LEVI E.Space vector PWM for a five-phase VSI supplying two five-phase series-connected machines［C］//12th International Power Electronics and Motion Control Conference，August 30－September 1，2006，Portoroz，Slovenia.2006:222－227.

［5］LEVI E.Even-phase multi-motor vector controlled driver with single inverter supply and series connection of stator windings［J］.IEE Proceedings-Electric Power Applications，2003，150(5):580－591.

［6］SEMAIL E，LEVI E，BOUSCAYROL A，et al.Multi-machine modeling of two series connected 5-phase synchronous machines:effect of harmonics on control［C］//European Conference on Power Electronics and Applications，September 11－14，2005，Dresden，Germany.2005:1－10.

［7］LEVI E，JONES M，VUKOSAVIC S N，et al.Stator winding design for multi-phase two-motor drives with single VSI supply［C］//International Conference on Electrical Machines，September 2－5，2006，Chania，Greece.2006:CD－ROM Paper No.OMM2－1.

［8］艾永樂，王玉梅，KAMPER Marrten.梯形波相電流控制的六相感應電機建模與控制［J］.電機與控制學報，2012，16(3):71－76.

AI Yongle，WANG Yumei，KAMPER Marrten.Modeling and controlling of six-phase induction machine driven trapezoidal phase current waveform［J］.Electric Machines and Control，2012，16(3):71－76.

［9］彭兵，王成元，夏加寬.六相永磁力矩伺服電機氣隙磁場優化［J］.電機與控制學報，2011，15(12):39－42.

PENG Bing，WANG Chengyuan，XIA Jiakuan.Air-gap magnetic field optimization for six-phase permanent magnet torque servo motor［J］.Electric Machines and Control，2011，15(12):39－42.

［10］楊金波，楊貴杰，李鐵才.雙三相永磁同步電機的建模與矢量控制［J］.電機與控制學報，2010，14(6):1－7.

YANG Jinbo，YANG Guijie，LI Tiecai，Modeling and vector control for dual three-phase PMSM［J］.Electric Machines and Control，2010，14(6):1－7.

［11］歐陽紅林，成蘭仙.多相永磁同步電機模糊神經網絡控制調速系統［J］.電機與控制學報，2007，11(2):111－115.

OUYANG Honglin，CHENG Lanxian.Multiple phase permanent magnet synchronous motor speed control system based on fuzzy neural network control［J］.Electric Machines and Control，2007，11(2):111－115.

［12］趙品志，楊貴杰，李勇.三次諧波注入式五相永磁同步電機轉矩密度優化［J］.中國電機工程學報，2010，30(33):71－77.

ZHAO Pinzhi，YANG Guijie，LI Yong.Torque density optimization for five-phase PMSM with third harmonic injection［J］.Proceedings of the CSEE，2010，30(33):71－77.