平面微彈簧性能比較研究

程建建,聶偉榮,周織建,黃慶武

(南京理工大學機械工程學院,江蘇南京210094)

0 引言

微彈簧是 MEMS(micro electro-mechanical systems)器件中重要部件,為微器件提供彈性力[1]。由于現有MEMS器件加工技術限制,微彈簧多為平面結構[2]。C型[3],S型[1,4,5],W 型[4,5]為三種典型平面微彈簧類型。 C 型彈簧多用于多軸向慣性開關[6－7]器件設計,文獻[8,9]中結構采用了S型彈簧設計,文獻[10]中安全預警機構采用W型彈簧設計。相對于C型彈簧,S型與W型彈簧在作用力方向位移量較大。微機電系統中結構尺寸受放置空間限制[5]。對于結構尺寸固定在一定范圍的微彈簧,根據器件設計需求的彈性系數,選擇最優的彈簧類型,以充分利用有限的尺寸空間。文獻[5]中在相等的水平方向外輪廓長度、線寬、直粱間距以及結構厚度條件下,表明S型彈簧柔度小于W型平面彈簧柔度。在文獻[5]中S型彈簧與W型彈簧比較方法中,兩種類型彈簧占用結構面積不同,不能更確切地反映彈簧彈性性能。本文在相等的結構面積情況下,分析C型、S型以及W型彈簧中任意兩種彈簧柔度系數比的對數值分布情況。

1 微平面彈簧結構參數

C型彈簧的結構參數,如圖1(a)所示。B為彈簧線寬,H為結構深度,R為彎曲半徑。C型彈簧應用形式多為單節并聯,因此彈簧節數為1。在平面微兩軸向開關中,集中力Fx、Fy分別作用在C型彈簧自由端,彈簧另一端固定。

S型彈簧結構參數,如圖1(b)所示。平面S型微彈簧由n個結構相同的U型單元組成,集中力Fy作用在平面S型彈簧的第一個U型單元的頂端相連接,第n個U型單元底端固定。B為彈簧線寬,L為彈簧U型單元直梁長度,R為彈簧彎曲半徑,H為結構厚度。

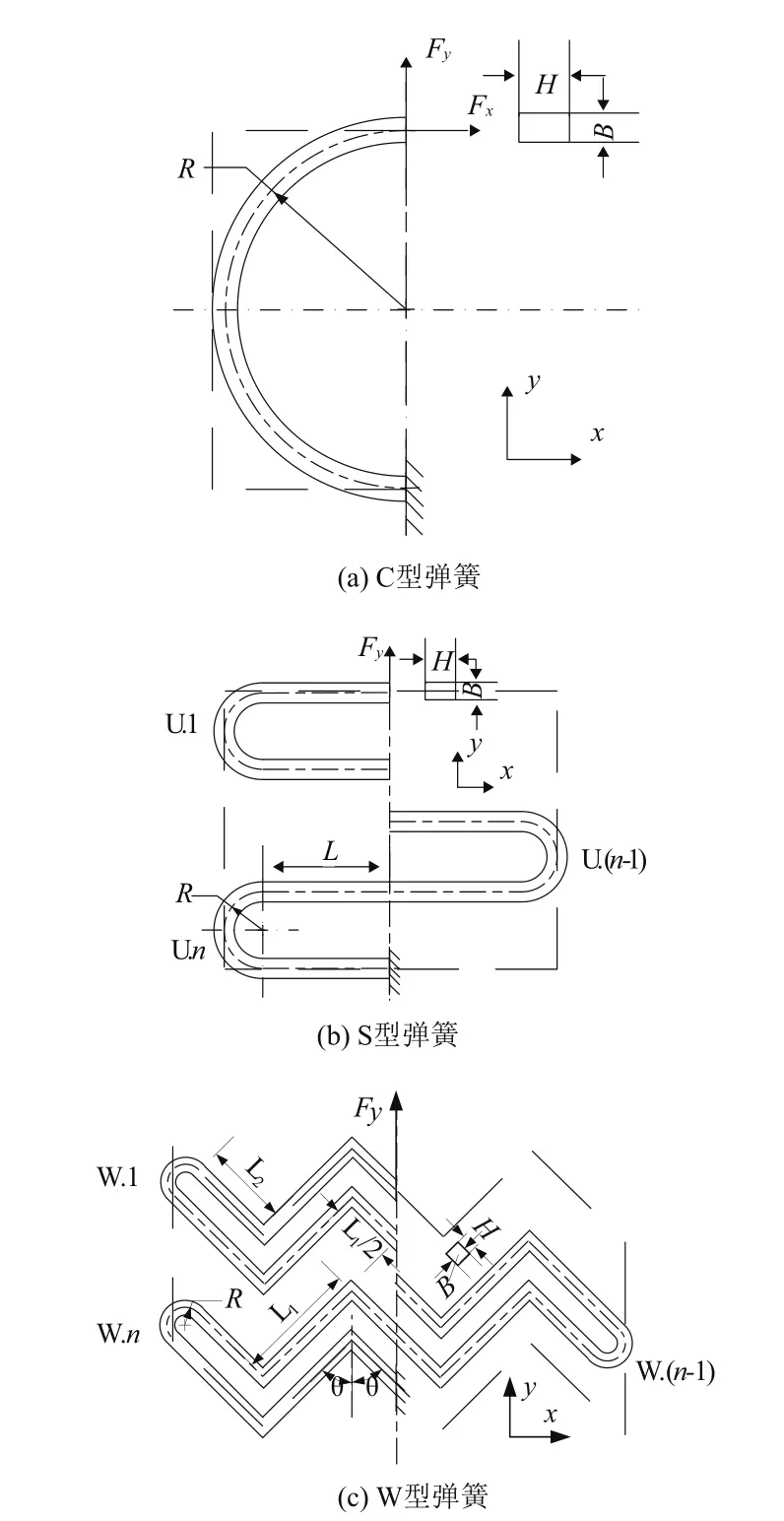
圖1 彈簧結構參數

W型彈簧的結構參數,如圖1(c)所示。W型彈簧由n個結構相同W型單元組成,集中力Fy作用在平面W型第W.1彈性單元的自由端,第W.n彈性單元底端固定。B為彈簧線寬,L1、L2為彈簧W型單元彎梁長度,R為彈簧彎曲半徑,H為結構厚度,2θ為彎梁夾角。

2 微平面彈簧性能分析

在兩種彈簧材料彈性模量E與彈簧截面慣性矩I(I＝B3H/12)分別相等情況下,引入彈簧柔度性能比較系數λ,如式(1)所示:

式中:δ1為彈簧1柔度系數,δ2為彈簧2柔度系數,S1為彈簧1占用結構面積,S2為彈簧2占用結構面積。

λ表示在彈簧1與彈簧2在相等彈簧結構面積情況下,彈簧柔度系數比的對數值。λ<0,彈簧1柔度系數小于彈簧2柔度系數;λ＝0,彈簧1柔度系數等于彈簧2柔度系數;λ>0,彈簧1柔度系數大于彈簧2柔度系數。λ也表示在相等彈簧柔度系數情況下,彈簧2與彈簧1占用結構面積比的對數值。λ<0,彈簧1結構面積大于彈簧2結構面積;λ＝0,彈簧1結構面積等于彈簧2結構面積;λ>0,彈簧1結構面積小于彈簧2結構面積。

S型彈簧與C型彈簧x軸向、y軸向柔度性能比較系數

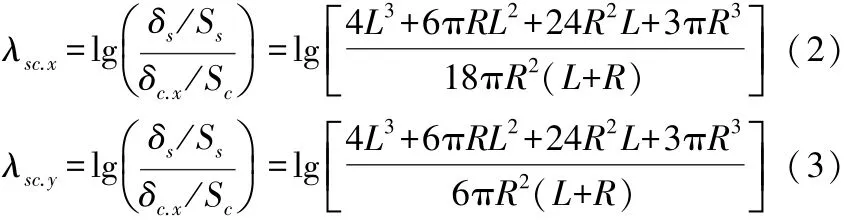
式中:δs為由n個U型單元組成S型彈簧的柔度系數,其值為 δs＝n(4L3＋6πRL2＋24R2L＋3πR3)/(6EI);δc.x、δc.y分別為C型彈簧x軸向與y軸向系數柔度系數,其值分別為δc.x＝3πR3/(2EI), δc.y＝πR3/(2EI),Ss為 S 型彈簧占用的結構面積(如圖1－b虛線包圍矩形框面積),其面積為Ss＝4nR(L＋R);Sc為C型彈簧占用的結構面積(如圖1－a虛線包圍矩形框面積),其面積為Sc＝2R2。

根據式(2)、式(3)可知,λsc.x、λsc.y與 E、I無關,僅與L、R有關。 由于 λsc.y－λsc.x＝lg3,S型彈簧柔度系數與 C 型彈簧y軸向系數λsc.y與x軸向系數λsc.x性能類似,因此本文只分析C型彈簧x軸向系數。

S型彈簧與C型彈簧x軸向柔度性能比較系數λsc.x等高線,如圖2所示。 當 R/L｜λsc.x＝0＝0.49時,S型彈簧與 C型彈簧在相等結構面積情況下,S型彈簧提供的柔度系數與C型彈簧提供的x軸向柔度系數相等(即S型彈簧與C型彈簧可相互替換)。當R/L<0.49時,λsc.x>0,S型彈簧柔度系數大于C型彈簧x軸向柔度系數;當R/L<0.099時,λsc.x>1,S型彈簧柔度系數遠大于C型彈簧x軸向柔度系數,對于微系統要求較低彈性系數時,優先選擇S型彈簧。當R/L>0.49時,λsc.x<0,S型彈簧單位面積提供的柔度系數小于C型彈簧單位面積提供的x軸向柔度系數。對確定的柔度系數,C型彈簧占用的面積較小,有利于系統整體結構的小型化。

圖2 S型彈簧與C型彈簧柔度性能比較系數

C型彈簧x軸向柔度與W型彈簧柔度性能比較系數:

式中:δw為有n節W型彈性單元組成W型彈簧柔度系數,其值為

Sw為n節W型彈簧所占結構面積,其值為Sw＝4nR(L＋R＋Rcotθ);W 型彈簧彎梁等效長度為 L＝3L1/2＋L2。

根據式(4)可得λcw.x與彎梁等效長度L、彎曲半徑R以及夾角θ有關。如表1所示,在C型彈簧與W型彈簧柔度性能比較系數λcw.x＝0情況下,直線λcw.x＝0隨夾角θ增大,R/L先增后減,夾角 θ＝60°時,出現波峰,在夾角θ＝90°,出現波谷,波峰與波谷間波動較小,因此近似認為直線 R/L｜λcw.x＝0≈0.52 近似不變。 在夾角 θ＝90°時,C 型彈簧與W型彈簧柔度性能比較系數λcw.x和S型彈簧與C型彈簧柔度性能比較系數λsc.x互為相反數。

表 1 夾角 θ 與 R/L｜λcw.x＝0關系

如圖3所示,當R/L<0.52時,比較系數λcw.x<0,C型彈簧單位面積x軸向柔度系數小于W型彈簧單位面積柔度系數,在固定設計彈性系數指標情況下,W型彈簧結構面積較小;在R/L>0.52時,彈簧柔度性能與R/L<0.52情況相反。夾角θ＝30°時,比較系數λcw.x＝0附近區域非零比較系數變化較為平坦,隨著夾角θ增加,柔度性能比較系數梯度增強,非零比較系數向λcw.x＝0靠近。但在λcw.x>2時,比較系數λcw.x不隨R/L改變而改變。

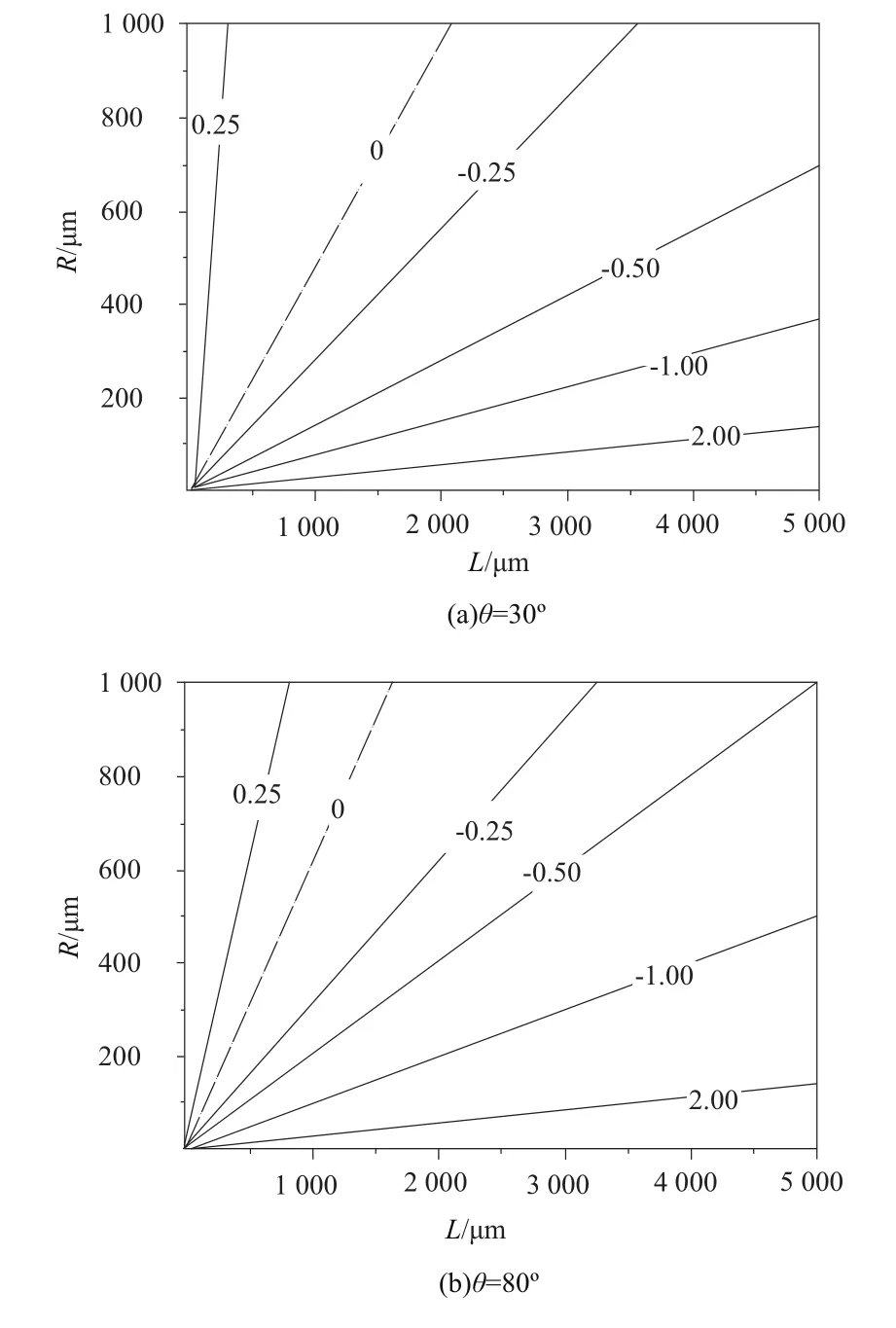
圖3 C型彈簧與W型彈簧柔度性能比較系數

S型彈簧與W型彈簧柔度性能比較系數

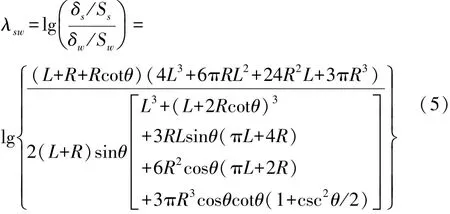
在S型彈簧與W型彈簧柔度性能比較系數λsw＝0情況下,夾角 θ與R/L關系,如表2所示。 與 R/L｜λsc＝0以及R/L｜λcw.x＝0為常數不同,在夾角 0<θ<30°情況下,S 型彈簧與 W 型彈簧 R/L｜λsw＝0,隨夾角 θ增大而增大;在夾角30°<θ<90°情況下,R/L｜λsw＝0隨夾角 θ增大而減小。 因此夾角θ＝30 °時,R/L｜λsw＝0取得最大值 0.46。 當夾角 θ＝90 °時,比較系數λsw≡0,與R/L無關,即S型彈簧為夾角θ＝90°的W型彈簧特例。

表 2 夾角 θ 與 R/L｜λsw＝0關系

如圖4(a)所示,在夾角 θ＝30°時,R/L>0.46,S 型彈簧單位面積的柔度系數小于W型彈簧柔度系數;R/L<0.46,S型彈簧單位面積的柔度系數大于W型彈簧柔度系數。λsw.max＝－0.467,λsw.min＝0.3,S 型彈簧柔度性能比較系數變化梯度小于W型彈簧。

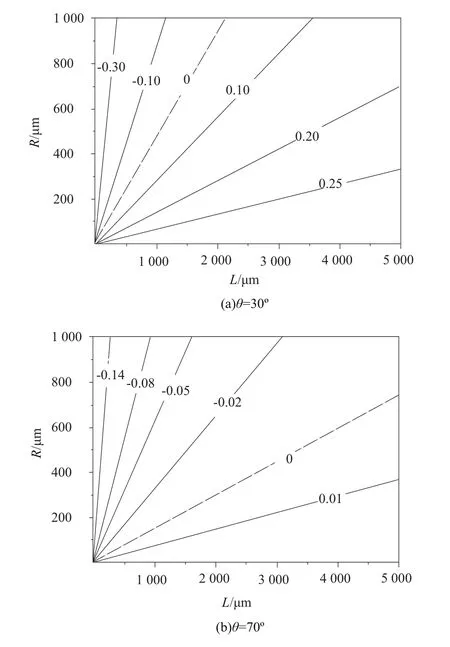
圖4 S型彈簧與W型彈簧柔度性能比較系數

根據圖4(b)可得,在夾角 θ＝70°時,R/L>0.13,S 型彈簧單位面積的柔度系數小于W型彈簧柔度系數,S型彈簧單位柔度的結構面積大于W型彈簧結構面積;R/L<0.13,S型彈簧單位面積的柔度系數較大以及單位柔度的結構面積較小。W型彈簧單位柔度的所占用結構面積小于S型彈簧比較系數斜率范圍增大(R/L｜λsw＝0＝0.13)。 根據｜λsw｜θ＝70°｜＝ 0.19< ｜λsw｜θ＝30°｜,可知夾角70°<θ<90°時,可近似認為S型彈簧與W型彈簧可相互替代。

選取C型彈簧的結構參數為:彈簧線寬B＝40 μm、結構深度 H＝50 μm、彎半徑 R＝100 μm,S型彈簧的結構參數為:彈簧線寬 B＝40 μm、結構深度 H＝50 μm、彎半徑R＝100 μm、直粱 L＝1 000 μm,W 型彈簧結構參數為:彈簧線寬 B＝40 μm、結構深度 H＝50 μm、彎半徑 R＝100 μm、彎梁長度 L1＝400 μm、L2＝ 400 μm,夾角 θ＝60°。 選用鎳材料的彈性模量E＝1.6×1011Pa,泊松比μ＝0.312。利用仿真軟件對比較系數進行驗算,彈簧性能比較系數理論值、仿真值以及理論值與仿真值相對誤差,如表3所示。彈簧柔度比較系數λ理論值與仿真值的相對誤差小于5%,上述公式可信。

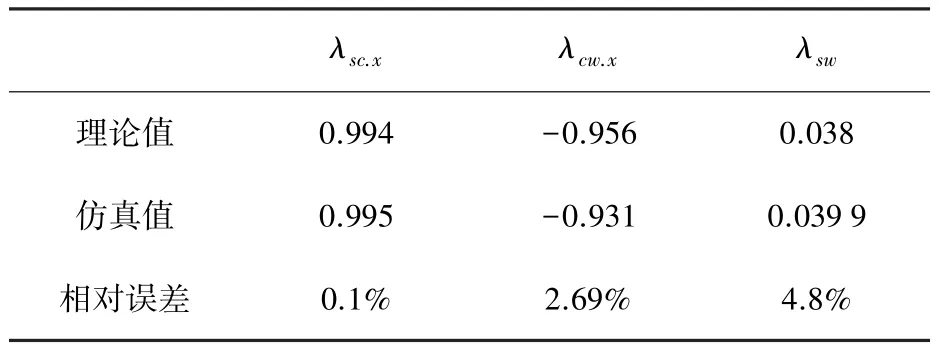
表3 C型、S型、W型彈簧柔度性能比較系數

綜上所述, R/L0.52,C型彈簧單位結構面積可提供柔度系數最大,其次為W型彈簧,S型彈簧最小;S型彈簧單位彈性系數所占用結構面積最大,其次W型彈簧,C型彈簧最小。

3 結語

本文提出了彈簧柔度性能比較系數,通過在相等的彈簧占用結構面積情況下,分析彈簧C型、S型以及W型彈簧中任意兩種彈簧柔度系數比的對數值分布情況。利用有限元仿真軟件驗證了彈簧柔度性能比較系數公式正確性。分析了直粱、彎梁長度、彎曲半徑以及彎梁夾角對彈簧柔度性能比較系數的影響,表明了在S型彈簧與C型彈簧柔度性能比較系數以及C型彈簧與W型彈簧柔度性能比較系數為零情況下,彎梁夾角和彎半徑與直粱(彎梁等效直粱長度)比值無關;在S型彈簧與C型彈簧柔度性能比較系數為零情況下,隨夾角增大,彎半徑與直粱比值先增大后減小。彎半徑與直粱比值大小影響C型、S型、W型彈簧單位結構面積柔度系數順序排列。為平面微彈簧的優化設計提供一定的理論依據。

[1]何光,石庚辰.MEMS彈簧特性的有限元分析[J].微計算機信息,2006,22(2):158-160.

[2]Agel D.J,Materials and Processes for Microsystems[J].Surface and Coatings Technology, 1998, 32(3):1032104.

[3]吳鵬飛,張國俊,鐘志親,等.C型MEMS平面微彈簧彈性系數研究[J].壓電與聲光,2012,34(3):470-472.

[4]吳志亮,常娟,馮鵬洲,等.引信用MEMS平面微彈簧彈性系數分析[J].南京理工大學學報(自然科學版),2008,32(2):140-143.

[5]何光,石庚辰.平面S型與平面W型MEMS彈簧性能比較研究[J].傳感技術學報, 2008,21(2):288-291.

[6] Currano L.J., Becker C.R., Smith G.L.et al.3-Axis Acceleration Switch for Traumatic Brain Injury Early Warning.Paris, France:MEMS 2012,2012:484-487.

[7] Greywall D.S.MEMS-based Inertial Switch[P].USA:NO7218193B2,2007.

[8]Yang Z.Q,Cai H.G,Ding G.F,et al.Dynamic Simulation of A Contact-Enhanced MEMS Inertial Switch in Simulink[J].Microsyst Technol, 2011, 17:1329-1342.

[9]Liu H.C, Lee C.K, Kobayashi T, et al.A New S-shaped MEMS PZT Cantilever for Energy Harvesting from.

[10]Robinson CH, Wood RH, Hoang TQ.Miniature MEMS-based electro-mechanical safety and arming device[P] .USA:NO6964231B1,2005.