Klein-Gordon-Schr?dinger耦合方程的線性化緊致差分格式

孫啟航, 徐尚巧

(魯東大學 信息與電氣工程學院,山東 煙臺 264025)

0 引言

在量子場論中,非線性Klein-Gordon-Schr?dinger(KGS)耦合方程刻畫了守恒復中子場和中性介子場Yukawa相互作用的經典模型[1-2]．許多作者從解的性質、類型以及數值解法等方面研究了這類方程[1-6]．文獻[5,7-8]中給出了KGS耦合方程的孤立波解、平面波解以及周期解．在數值方面,Xiang[9-10]利用譜方法對此方程進行了研究,并給出了該方法的誤差估計．Wang等[11]利用樣條配置方法給出了該方程的數值解．Bao等[12]將時間分裂譜離散的方法作用于KGS方程,也得到了較好的數值結果．張魯明等[13-15]構造了關于KGS方程的守恒差分格式,其收斂階為O(τ2+h2).本文介紹一個新的緊致差分格式,該格式是線性化的并且解耦的,其收斂階為O(τ2+h4),并通過理論以及數值試驗證明格式的正確性．

考慮如下KGS耦合方程的周期邊值問題:

(1)

utt-uxx+u-|φ|2=0,

(2)

φ(x,0)=φ0(x),u(x,0)=u0(x),ut(x,0)=u1(x),

(3)

φ(x,t)=φ(x+L,t),u(x,t)=u(x+L,t), 0≤t≤T,

(4)

其中φ和φ(x,t)是未知的復值函數,u和u(x,t)是未知的實值函數,常數L為方程的周期．

1 預備知識

1.1 符號的定義

為了更方便地解決KGS耦合方程的周期邊值問題,定義如下記號:

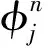
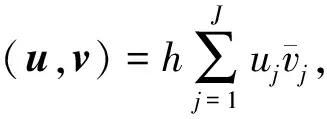
對于所研究的非線性KGS耦合方程的周期邊值問題(1)～(4)的精確解,假設

max{‖un‖,‖δxun‖,‖un‖∞}≤C, max{‖φn‖,‖δxφn‖,‖φn‖∞}≤C,

經過簡單計算可知,此周期邊值問題滿足如下守恒性質:

Q(t)=‖φ‖2=Q(0),

(5)

(6)

1.2 幾個引理

引理1[16]對任意的網格函數u,v∈Vh,且滿足uj=uj+J,vj=vj+J,則有

引理2[16](Gronwall不等式) 假設網格函數{wn|n=0,1,2,…,N;Nτ=T}滿足不等式

其中A和Bl(l=0,1,2,…,N)是非負常數,則

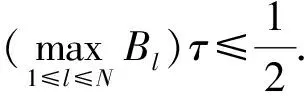
引理3[16]假設網格函數{wn|n=0,1,2,…,N;Nτ=T}滿足不等式

wn-wn-1≤Aτwn+Bτwn-1+Cnτ,

其中A,B和Cn(n=0,1,2,…,N)是非負常數,則

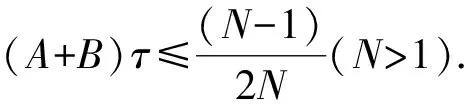
引理4[16]對于序列w={w0,w1,…,wn-1,wn}和g={g0,g1,…,gn-1,gn},有

引理5[16]對任一實值對稱正定矩陣HJ×J,un∈Vh,則

其中RJ×J是一個對H進行Cholesky分解得到的上三角實值矩陣,即……