食餌具有階段結構的時滯捕食系統(tǒng)的Hopf分支控制

劉 娟， 孫禮俊

(蚌埠學院 數(shù)學與物理系,安徽 蚌埠 233030)

0 引言

捕食系統(tǒng)在種群動力學建模中非常重要,多年來受到國內外許多學者的關注[1-3]．但是,在傳統(tǒng)的捕食系統(tǒng)模型中,都假設食餌對捕食者的威脅具有相同的抵御能力．這種假設對于許多動物種群來說是很不現(xiàn)實的．因此,近年來具有階段結構的捕食系統(tǒng)模型受到學者的關注[4-9]．文獻[6]研究了一類食餌具有階段結構的時滯捕食系統(tǒng)模型

(1)

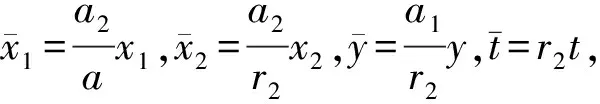
(2)

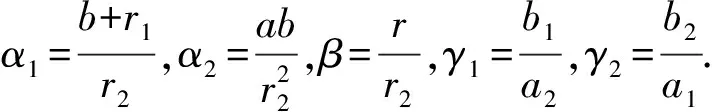
文獻[6]研究了系統(tǒng)(2)的Hopf分支問題,得到了系統(tǒng)(2)產生Hopf分支的充分條件．Hopf分支是一種重要的非線性現(xiàn)象,而這種現(xiàn)象的發(fā)生可能對動力系統(tǒng)造成難以估計的有害影響．基于此,本文針對系統(tǒng)(2),利用狀態(tài)反饋和參數(shù)擾動設計Hopf分支控制器,研究受控系統(tǒng)的Hopf分支,其模型如下：

(3)

其中α′和β′是對系統(tǒng)Hopf分支進行控制的參數(shù)．

1 受控系統(tǒng)的Hopf分支存在性

顯然,系統(tǒng)(3)和(2)具有相同的平衡點．由文獻[6]知,如果系統(tǒng)(3)滿足條件

H1)α2-(1+βγ1)α1>0,

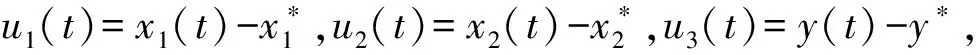
(4)

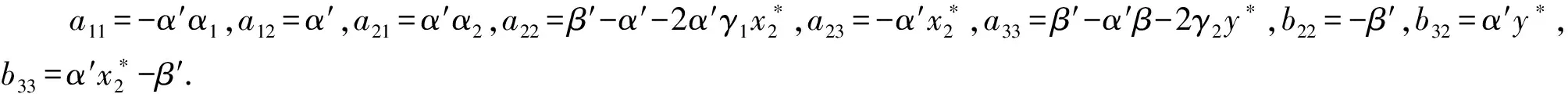
系統(tǒng)(4)的特征方程為

λ3+A2λ2+A1λ+A0+(B2λ2+B1λ+B0)e-λτ+(C1λ+C0)e-2λτ=0,

(5)

其中

A0=(a12a21-a11a22)a33,A1=a11a22-a12a21+(a11+a22)a33,A2=-(a11+a22+a33),

B0=a11(a23b32-a33b22)+b33(a12a21-a11a22),B1=b22(a11+a33)+b33(a11+a22)-a23b32,

B2=-(b22+b33),C1=b22b33,C0=a11b22b33.

方程(5)兩邊同時乘以eλτ,得到

B2λ2+B1λ+B0+(λ3+A2λ2+A1λ+A0)eλτ+(C1λ+C0)e-λτ=0,

(6)

當τ=0時,方程(6)變?yōu)?/p>

λ3+(A2+B2)λ2+(A1+B1+C1)λ+A0+B0+C0=0.

(7)

根據(jù)赫爾維茨定理,如果

H2)A2+B2>0,且(A2+B2)(A1+B1+C1)>A0+B0+C0,

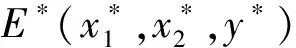
當τ>0時,令λ=iω(ω>0)為特征方程(6)的根,代入(6)并分離實虛部得

(8)

從而,有

(9)

其中

n5=B2,n3=A2B1-A1B2-B2C1-B0,n1=A1B0+B0C1-A0B1-B1C0,

n4=B1-A2B2,n2=(A0-C0)B2+(C1-A1)B1+A2B0,n0=B0(C0-A0),

進而,得到

ω12+e5ω10+e4ω8+e3ω6+e2ω4+e1ω2+e0=0,

(10)

其中

令ω2=v,方程(10)變?yōu)?/p>

v6+e5v5+e4v4+e3v3+e2v2+e1v+e0=0.

(11)

下面給出如下假設:

H3) 方程(11)存在6個正根,分別表示為v1,v2,v3,v4,v5和v6,

對于每個特定的ωk,根據(jù)(9),可以得到

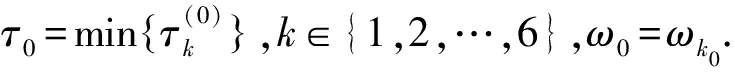
方程(6)的兩端分別對τ進行求導,得到

因此

其中

顯然,如果

H4)PRQR+PIQI≠0,

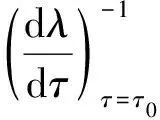
根據(jù)文獻[9]中的Hopf分支定理,得到下列結果．

定理1對于受控系統(tǒng)(3),如果H1)～H4)成立,則

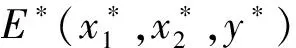
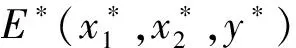
2 數(shù)值模擬

對受控系統(tǒng)(3)進行數(shù)值模擬,系統(tǒng)參數(shù)選取如下:

α1=0.5,α2=2,β=1,γ1=0.25,γ2=0.5,α′=0.2,β′=0.4.

得到受控系統(tǒng)

(12)

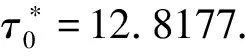
圖1 當τ=……