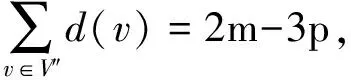On geometric-arithmetic index of line graph
Liu Keqiang, Zhao Biao
(College of Mathematics & System Sciences,Xinjiang University,Urumqi 830046,Xinjiang,China)
0 Introduction
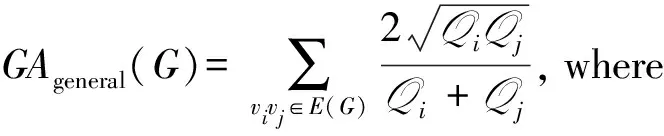
The chemical applicability of theGA1index was examined documented in detail in the paper [8] and the reviews [9-10]. Upper and lower bounds forGA1index of general graphs have been given in [4,11-12]. In this paper, the sharp upper and lower bounds onGA1index of line graph are obtained.
LetE′={(u1v,vu2)|u1v,vu2∈E(G)}, call graph (E(G),E′) as line graph ofG, denotedL(G). Denote the edge ofL(G) by (u1,v,u2), both (u1,v,u2) and (u1,v,u2) demonstrate the same edge. LetP={(u1,v,u2)∈E(L(G))|u1v,vu2∈E(G),d(u1)=1,d(v)=2} be the set of pendant edges,Γ={H|u1,v,u2∈V(H) andu1v,vu2∈E(H) such thatd(u1)=1,d(v)=2,d(u2)=Δ=δ1} be the class of graphH.
1 Some lemmas
Lemma1[13]Let (a1,a2,…,an) be the positiven-tuples such that there exist positive numbersaandAsatisfying 0 (1) Lemma4[14]LetGbe a graph withnvertices andmedges,anddvdenote the degree of a vertexvinG,then ii) the degree inL(G) of an edgeuvofGisd(u)+d(v)-2. Theorem1LetGbe a simple connected graph of ordernwithmedges, maximum vertex degreeΔand minimum vertex degreeδ,δ≥2, then GA1(L(G))≥GA1(G), (2) with equality holding if and only ifG?Cn. ProofDefine the index For 2≤d(u1),d(v),d(u2)≤Δ, we have (3) with equality holding if and only ifd(u2)=d(v)=Δ=2.Thus (4) Forv∈V(G), we have (5) Thus (6) Now suppose that equality holds in (2),then all inequalities in the above argument must be equalities, from equality (5) and (6), we have forv∈V(G),d(v)=2, that isG?Cn. Conversely, we can see easily that the equality holds in (2) forG?Cn. Theorem2LetGbe a simple connected graph of ordernwithmedges,ppendent edges, maximum vertex degreeΔ, minimum vertex degreeδ1of non-pendent edge, (d1,d2,…,dm) be a degree sequence ofL(G). Then (7) with equality holding if and only ifGis isomorphic to a regular graph orG∈Γ. ProofDefine the index For brevity, write Forδ1≤d(u1),d(v),d(u2), we have This implies and finally we get (8) Now since Note that |E′-P|=e(L(G))-p, using (1), we get (9) BecauseP={(u1,v,u2)|u1v,u2v∈E(G),d(u1)=1,d(v)=2}, then |P|=p, we have (10) Thus (11) (12) with equality holding if and only ifΔ=δ1(for allv∈V″, thend(v)=(2m-3p)/(n-2p)). Forδ1≤d(u2)≤Δ, we have (13) From (10)-(13), we get (7). Suppose that equality holds in (7), then all inequalities in the above argument must be equalities. Now we consider two case: i) ifp=0, from equality in (8), we getΔ=δ1. ThenGis isomorphic to a regular graph. ii) ifp>0, from equality in (10) and (13), we getd(u1)=1,d(v)=2,d(u2)=Δ=δ1, thusG∈Γ. Conversely, one can easily see that the equality holds in (7) for regular graph orG∈Γ. Theorem3LetGbe a simple connected graph of ordernwithmedges,ppendant edge. Then (14) with equality holding in (14) if and only ifGis isomorphic to the complete graphK3orG?P3orG?P4. ProofFor each pendant edge (u1,v,u2)∈E′,we have eitherd(u1)=1,d(v)=2 ord(u2)=1,d(v)=2.Thus and finally we get (15) with equality holds in (15) if and only ifd(u1)=1,d(v)=2,d(u2)=n-2. For each non-pendant edge (u1,v,u2)∈E′, we have 2≤d(u1),d(v),d(u2)≤n-1. Thus then (16) with equality holds in (16) if and only ifd(u1)=2,d(v)=2,d(u2)=n-1.Thus Suppose that equality holds in (14), then all inequalities in the above argument must be equalities. Now we consider two case i) ifp=0, from equality (16), we getd(u1)=2,d(v)=2,d(u2)=n-1. Then we have a common neighborv. ThusGis isomorphic to the complete graphK3. ii) ifp>0, from equality (16), we getd(u1)=1,d(v)=2,d(u2)=n-2. Firstly, assume thate(L(G)) =p, then all the edges are pendant edges inL(G), and henceGis isomorphic toP3orP4. Next, assume thate(L(G))>p. In this case, the maximum degree vertex, sayu2,by equality in (16) has degreen-1. There exists at least one non-pendant edge inG, and hence two vertices, sayviandvj, are adjacent to vertexu2. By equality in (16), for the non-pendant edgevivj∈E(G), eitherdi=n-1 ordj=n-1. Thus do not have any pendant vertex inGasdi=n-1, that is a contradiction. Conversely, we can easily see that the equality holds in (14) for the complete graphK3orG?P3orG?P4. Theorem4LetGbe a simple connected graph withnvertices,medges,ppendant edges,maximum vertex degreeΔand minimum vertex degreeδ1of non-pendant edge,(d1,d2,…,dm) be a degree sequence ofL(G).Then (17) with equality holding in (17) if and only ifGis isomorphic to a regular graph orG∈Γ. ProofFor each pendant edge (u1,v,u2)∈E′,we have eitherd(u1)=1,d(v)=2 ord(u2)=1,d(v)=2.By Lemma 1,we have (18) with equality holds in (18) if and only ifd(u1)=1,d(v)=2,d(u2)=δ1. Sincee(L(G))-pis the number of non-pendant edges inL(G). By Cauchy-Schwarz Inequality, we get (19) Note that |V″|=n-2p, by lemma 4, we have (20) with equality holds in (20) if and only if for ?v∈V″,d(v)=Δ. From (18),(19) and (20), we get (17). Suppose that equality holds in (17), then all inequalities in the above argument must be equalities. Now we consider two case: i) ifp=0, from equality (19),(20), we getd(u1)=d(v)=d(u2)=Δ=δ1.That is,Gis isomorphic to a regular graph. ii) ifp>0, from equality (18)-(20), we getd(u1)=1,d(v)=2,d(u2)=Δ=δ1. That is,G∈Γ. Conversely, one can easily see that the equality holds in (17) for a regular graph orG∈Γ. : [1] Dankelmann P,Gutman I,Mukwembi S,et al.On the degree distance of a graph[J].Discrete Appl Math,2009,157(13):2773. [2] Das K C,Gutman I.Estimating the wiener index by means of number of vertices,number of edges and diameter[J].MATCH Commun Math Comput Chem,2010,64:647. [4] Todeschini R,Consonni V.Molecular descriptors for chemoinformatics.Vol 41[M].Weinheim:Wiley-VCH,2009. [5] Das K C.Atom-bond connetivity index of graphs[J].Discrete Appl Math,2010,158(11):1181. [7] Horoldagva B,Lee S G.Comparing Zagreb indices for connected graphs[J].Discrete Appl Math,2010,158(10):1073. [9] Das K C,Gutman I,Furtula B.Survey on geometric-arithmetic indices of graphs[J].MATCH Commun Math Comput Chem,2011,65:595. [10] Gutman I,Furtula B.Novel molecular structure descriptors:theory and applications.Vol Ⅰ[M].Kragujevac:University of Kragujevac,2010. [11] Das K C.On geometric-arithmetic index of graphs[J].MATCH Commun Math Comput Chem,2010,64:619. [12] Das K C,Gutman I,Furtula B.On the first geometic-arithmatic index of graph[J].Discrete Appl Math,2011,159(17):2030. [13] Pólya G,Szeg? G.Problems and theorems in analysis,series,integeral calulus:theory of functions.Vol Ⅰ[M].New York:Springer-Verlay,1972. [14] Beineke L W,Wilson R J.Selected topics in graph theory.Vol 2[M].New York:Academic Press Inc,1978.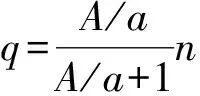
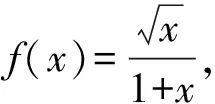
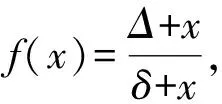
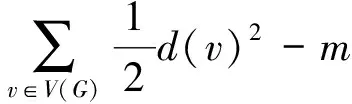
2 Bounds for GA1 index of line graph