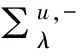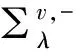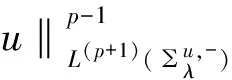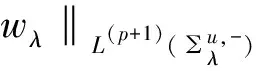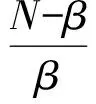積分方程組解的正則性與對稱性

王長森，林國煒

(江西師范大學數(shù)學與信息科學學院，330022，南昌)

積分方程組解的正則性與對稱性

王長森，林國煒

(江西師范大學數(shù)學與信息科學學院，330022，南昌)

將討論下列含貝塞爾核積分方程組正解的對稱性，即：

(1)

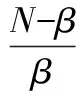
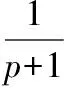
(2)

設(u,v)∈Lp+1(RN)×Lq+1(RN)為式(1)的正解，則式(1)解是徑向對稱的。

積分方程組；貝塞爾核；徑向對稱

0 引言

本文將討論下列含貝塞爾核積分方程組正解的對稱性，即：

(3)

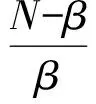
(4)

特別的，當u=v,p=q,β=τ=0時，式(3)簡化成：

(5)

在文獻[8]中，對于貝塞爾勢能的sobolevinepuality(Bα(f)=Gα*f,α>0;Bα(f)=f,α=0,這里*表示函數(shù)間的卷積)：

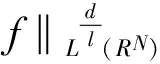
(6)

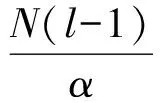
當β=τ=0時，在文獻[9]中討論了方程組(3)正解的徑向對稱性，同時也討論了當α=2,β=τ=0時解的唯一性。如果β≠0,τ≠0時，在文獻[9]中建立了關于貝塞爾勢能帶雙權Hardy-Littlewood-Sobolevinequality，即：

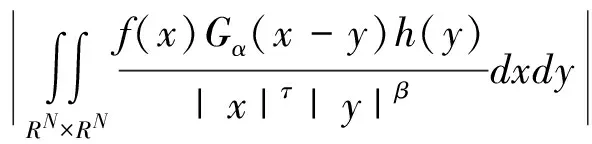
(7)

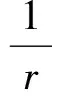
在文獻[6]中已證出下面積分方程組：

(8)

正解的徑向對稱性和局部H?lder連續(xù)性。

式(3)是關于式(7)的Euler-Lagrange方程。為了得到不等式式(7)中的最佳常數(shù)，定義最大函數(shù)：

在‖f‖r=‖h‖s=1的條件下，則對應的Euler-Lagrange方程為下面積分方程組：

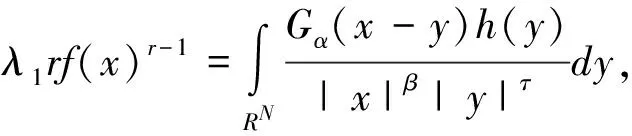
(9)

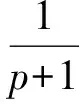
當貝塞爾核Gα(x)可以被Riesz核替代時，則式(3)就化成：

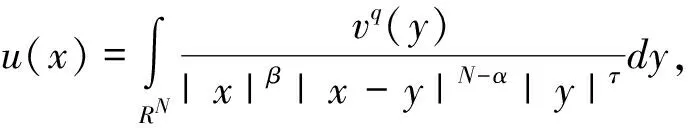
(10)

(11)

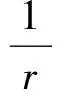
在文獻[4]中，通過移動平面法已證出方程組(10)正解的徑向對稱性。此外，研究者也采用在文獻[7]中的正則性提升方法，得出理想的積分區(qū)間和漸近性，讀者可以查閱在文獻[1-3,5,7,13-14]中更多的應用。

本文主要討論在式(4)條件下，式(3)正解的徑向對稱性，即：在(u,v)∈Lp+1(RN)×Lq+1(RN)為式(3)的正解，則解(u,v)是徑向對稱的。

1 引理及其命題

對于任意的實數(shù)λ，定義：∑λ={x=(x1,x2,…,xN)∈RN|x1≤λ},Tλ={x∈RN|x1=λ}。對于x∈∑λ，令xλ=(2λ-x1,x2,…,xN)，定義：uλ(x)=u(xλ),vλ(x)=v(xλ)。

引理1：對于式(3)的任意正解，有：

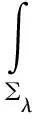
(12)

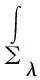
(13)

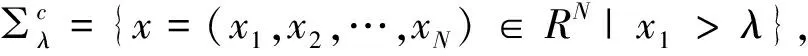
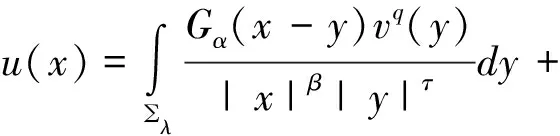
在上等式中應用了在RN中Gα是徑向對稱的，即有|xλ-y|=|x-yλ|，在上等式中x用xλ代替有：

因此，

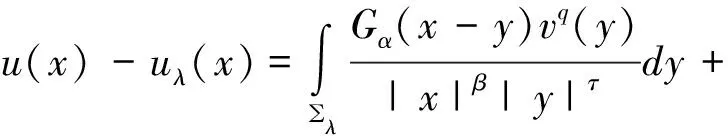
同理，v(x)-vλ(x)也是成立的。證畢。

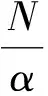
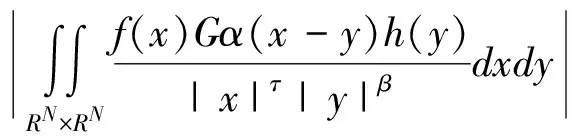
(14)

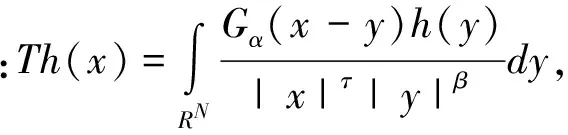
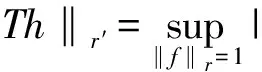
(15)

此命題的證明可參考文獻[6]。

2 主要結果及其證明

在這一部分，應用上述的引理及其命題證明出本文的主要結果，將采用文獻[2]中的移動平面法來證明本文的主要結果，本文主要結果如下。

定理1：設(u,v)為式(3)的任意一個正解，則此解是徑向對稱的，并且關于RN中某些點是單調(diào)遞減的。

證明：首先，證明對于充分小的負數(shù)λ，有：

u(x)≤u(xλ),v(x)≤v(xλ),?x∈∑λ

(16)

事實上，令：

通過對最新腦科學研究成果的解讀，我們可以看到腦科學的研究已經(jīng)走到了與其他多學科交叉的關鍵時刻，而且物理、化學等多種方法在腦科學研究中的運用一再突破腦科學的極限，使最終觀測大腦實時活動成為可能。

wλ(x)=u(x)-u(xλ),zλ(x)=v(x)-v(xλ)。

以及，

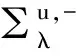
由于，

|x-y|<|xλ-y|,|y|>|yλ|,?x,xλ,yλ∈∑λ，

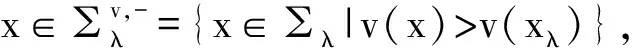
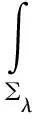
根據(jù)p,q>1以及式(4)知：

(17)

選擇合適的d1,d2使得：

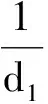
(18)

由式(4)可知：

(19)

因此，由命題1及H?ler不等式可推出：

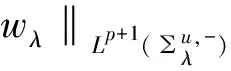
(20)

以及，

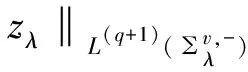
(21)

所以，

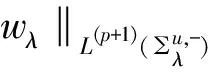
(22)

根據(jù)(u,v)∈Lp+1(RN)×Lq+1(RN),對于充分小的的負數(shù)λ，有：

因此有：

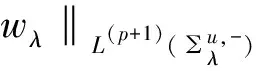
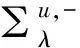
接下來，連續(xù)的增大λ的值，也就是說，在式(13)成立的條件下，將平面Tλ往右平移。下面將證明通過這樣移動平面Tλ，這種平移直到剛好平移到原點才停止。

事實上，令：

λ0=sup{λ|u(x)-uλ(x)≤0,v(x)-vλ(x)≤0,?x∈∑λ}

(23)

顯然λ0≤0,接下來斷言：

λ0=0

(24)

事實上，若λ0<0,則存在x0,x1∈∑λ0,使得：u(x0)=uλ0(x0),v(x1)=vλ0(x1)。由引理1及xλ0=(x0)λ0有：

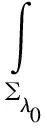
根據(jù)在∑λ0中，有|x0|>|xλ0|,|y|>|yλ0|,所以，在∑λ0中有：

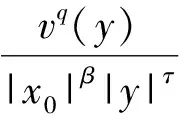
此外，在∑λ0中還有|x0-y|<|xλ0-y|，從而可知：

v(x)=vλ0(x)=0,a.e.x∈∑λ0

也就有v(x)≡0,這與v是正數(shù)就相矛盾，所以有：

u(x)

同理可證：

v(x)

由(u,v)∈Lp+1(RN)×Lq+1(RN),則對?ε>0,?R>0,使得：

由Lusin定理知，對?δ>0,?一個閉集Fδ滿足Fδ?BR(0)∪∑λ0=E,m(E-Fδ)<δ,使得wλ0|Fδ,zλ0|Fδ是連續(xù)的。

在∑λ0中有wλ0,zλ0<0,在Fδ中有wλ0,zλ0<0。選擇ε0>0并充分的小，使得對?λ∈[λ0,λ0+ε0)，在Fδ中有wλ,zλ<0，對于這樣的λ有：

選擇充分小的ε,δ,ε0，使得：

因此，

另一方面，采用同樣的方式，可將平面從x1方向的正無窮遠處往x1=0平移，這樣可得u(x),v(x)關于x1=0是徑向對稱及單調(diào)遞減的。此外，x1的方向可以是任意選取的，所以u(x),v(x)關于原點是徑向對稱的及嚴格單調(diào)的。證畢。

[1] Chen W,Li C.Regularity of solutions for a system of integral equations[J].Comm Pure Appl Anal,2005,4:1-8.

[2]Chen W,Li C,Ou B.Classification of solutions for an integral equation[J].Comm Pure Appl Math,2006,59:330-343.

[3]Chen W,Li C,Ou B.Classification of solutions for a system of integral equations[J].Comm PDE,2005,30:59-65.

[4]Jin C,Li C.Symmetry of solutions to some systems of integral equations[J].Proc Amer Math Soc,2006,134:1661-1670.

[5]Jin C,Li C.Qualitative analysis of some system of integral equations[J].Calc Var PDE,2006,26:447-457.

[6]Chen X,Yang J.Regularity and symmetry of positive solutions of an integral system[J].Acta Math Sci,2012,32B:1759-1780.

[7]Chen W,Jin C,Li C,etal.Weighted Hardy-Littlewood-Sobolev inequalities and systens of Integral equations[J].Disc Cont Dyn Sys,2005,suppl:164-172.

[8]Ma L,Chen D.Radial symmetry and montonicity for an integral equation[J].J Math Anal Appl,2008,342:943-949.

[9]Ma L,Chen D.Radial symmetry and uniqueness for positive solutions of a Schr? dinger type Systems[J].Mathematical and Computer Modelling,2009,49:379-385.

[10]Ma L,Zhao L.Uniqueness of ground states of some coupled nonlinear Schr?dinger systems and their application[J].J Diffe Equa,2008,245:2551-2565.

[11]Stein E,Weiss G.Fractional integrals in n-dimension Euclidean spaces[J].Journ Math Mech,1958,7:503-514.

[12]Li Y.Remark on some conformlly invariant integral equations:The method of moving spheres[J].J Eur Math Soc,2004,6:153-180.

[13]Xu J,Tan Z.Classification of solutions for a class of singuar integral system[J].Acta Mathematica Scientia,2011,31:1449-1456.

[14]Zhao Y,Lei Y.Asymptotic behavior of positive solutions of a nonlinear integral system[J].Nonlinear Anal,2012,75:1989-1999.

RegularityandSysmmetryofSolutionsofanIntegralSystems

WANG Changsen,LIN Guowei

(Jiangxi Normal University.College of Mathematic and Information Science,330022,Nanchang,PRC)

In this paper,we are concerned with symmetry of solutions of the following nonlinear integral system：

(1)

(2)

Let (u,v)∈Lp+1(RN)×Lq+1(RN) be a positive solution of(1).We show that the solution of(1) is symmetric.

integral system;bessel kernel;radially symmetry

2014-07-15;

2014-09-09

王長森(1989-)，男，江西上饒人，碩士研究生，主要從事帶權的積分方程的研究。

國家自然科學基金項目(編號:11361029)；江西省教育廳科學技術研究項目(編號:GJJ14270)。

10.13990/j.issn1001-3679.2014.05.002

O175.2

A

1001-3679(2014)05-0573-05