組合懲罰下聯合均值與方差模型的變量選擇

董 瑩, 宋 立 新, 石 新 勇

( 1.大連理工大學 數學科學學院, 遼寧 大連 116024；2.大連民族學院 理學院, 遼寧 大連 116600；3.中國人民解放軍68048部隊, 陜西 寶雞 721013 )

?

應用數學

組合懲罰下聯合均值與方差模型的變量選擇

董 瑩1,2, 宋 立 新*1, 石 新 勇1,3

( 1.大連理工大學 數學科學學院, 遼寧 大連 116024；2.大連民族學院 理學院, 遼寧 大連 116600；3.中國人民解放軍68048部隊, 陜西 寶雞 721013 )

在生產實踐和計量經濟領域中,控制產品質量的方差就能保證產品的合格品數相對穩定,所以當前學者對聯合均值與方差模型的研究倍感興趣．基于解釋變量經常是具有相關關系的實際情況,提出了一種由SCAD懲罰和嶺回歸混合在一起的組合懲罰,該懲罰充分利用了嶺回歸能克服解釋變量相關性過高對估計效果的影響,同時也證明了這樣的懲罰具有相合性和Oracle性質．使用該組合懲罰對聯合均值與方差模型進行了變量選擇．最后的隨機模擬結果表明該模型和方法是有效的．

組合懲罰；聯合均值與方差模型；變量選擇；懲罰極大似然估計

0 引 言

變量選擇是一種特殊的模型選擇問題,在統計研究中有著重要的意義．一般說來,根據問題本身的專業理論以及有關經驗,人們羅列出來的可能與因變量有關的自變量往往有很多,其中有一些變量對因變量根本沒有影響或影響很小．如果在建模中把這樣的一些變量都包括進來,不但計算量大,估計和預測的精度也會下降．而且實際問題中,某些自變量的獲得代價昂貴．因此,對模型自變量的選擇做一些理論分析很有必要．

目前,對均值回歸模型的變量選擇已有大量的文獻提出了相對成熟和有效的方法[1]．但是在回歸模型中,估計均值參數的有效性依賴于正確的模擬散布參數．因此對方差的討論能更好地解釋數據變化的原因和規律,這是數據分析中一個重要的發展趨勢．這種思想體現在經濟領域和質量管理等方面．控制期望值只表明性能指標的平均值合乎要求,但若方差比較大,則相當一部分產品仍然不合格,因而控制方差的大小與產品的合格率發生了緊密的聯系．因此,可以試著對方差建模,將方差也看作解釋變量的函數形式,進而了解方差的來源,知道哪些變量對方差具有主導作用．

最近幾年,許多統計學家對正態分布聯合均值與方差模型的研究也倍感興趣．Harvey[2]給出了聯合均值與方差模型的極大似然估計;Engel等[3]將聯合均值與方差模型應用到Taguchi的穩健試驗設計中;Smyth等[4]、Lee等[5],以及Wang等[6]在聯合均值與散布參數建模的框架下,研究了廣義線性模型和更廣泛分布的統計推斷．然而,對方差部分賦予一個模型結構后,關于均值和方差的聯合建模結構下的變量選擇問題尚待探討．

吳劉倉等[7-8]對聯合均值與方差模型的變量選擇進行了探討,得到了所提出的模型下的懲罰極大似然估計的優良性質以及其方法的有效性．本文在此模型下進一步探討一些具有高度相關關系的變量有可能對因變量具有很強的影響的情形．在實際情況中,解釋變量不相關的情況幾乎是不可能的,特別是在經濟及生物基因研究領域．Wang等[9]提出了組合懲罰(combined penalization,CP)．這一懲罰將平滑削邊絕對偏離(smoothly clipped absolute deviation,SCAD)懲罰和嶺回歸組合起來進行變量選擇,這種懲罰充分利用了嶺回歸能克服解釋變量相關性過高對估計效果的影響,同時也可以證明這樣的懲罰具有相合性和Oracle性質．

本文基于組合懲罰對聯合均值與方差模型進行變量選擇,實現對均值模型和方差模型同時進行變量選擇的目的．

1 基于組合懲罰下的極大似然估計變量選擇

1.1 聯合均值與方差模型

考慮聯合均值與方差模型

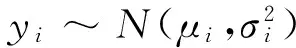
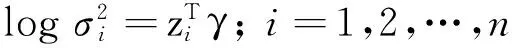
(1)

其中xi=(xi1xi2…xip)T和zi=(zi1zi2…ziq)T是解釋變量,yi是其相應的響應變量,β=(β1β2…βp)T是p×1的均值模型的未知參數向量,γ=(γ1γ2…γq)T是q×1的方差模型的未知參數向量．xi和zi可能包含不同或者相同的一些解釋變量,或者包含相同的解釋變量但卻具有不同的影響方式．

1.2 組合懲罰極大似然估計

假設(yi,xi,zi)(i=1,2,…,n)是來自聯合均值與方差模型的隨機樣本，記L(β,γ)為聯合均值與方差模型的對數似然函數，類似于文獻[10],可以定義組合懲罰似然函數為

(2)

其中λ和ι是調整參數,本文采用BIC準則來選擇調整參數．此處P′λn是SCAD懲罰函數且定義為

其中a>2,θ>0,Pλn(0)=0．

為了敘述簡便，重寫組合懲罰似然函數(2)為

(3)

其中θ=(θ1θ2…θs)T=(β1β2…βp

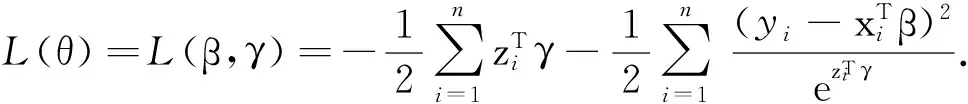
2 條件與性質

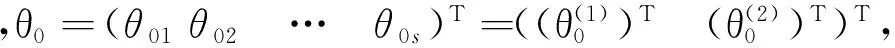
為了得到懲罰極大似然估計的相合性和漸進正態性，需要給出以下正則條件：

(1)xi=(xi1xi2…xip)T和zi=(zi1zi2…ziq)T(i=1,2,…,n)是固定的；

(2)參數空間是緊的，真實參數θ0為參數空間的內點；

(3)xi和zi在聯合均值與方差模型中是完全有界的,即它們中的所有分量是一個有限的實數；

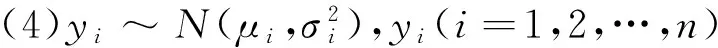
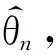
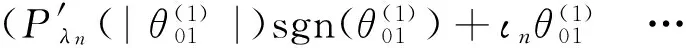
定理2懲罰函數滿足

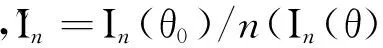
(2)(漸近正態性)

注1定理1和定理2的證明類似于文獻[10]．證明略．

注2定理2表明組合懲罰下的極大似然估計具有Oracle性質．

3 算 法

下面給出計算組合懲罰之下的聯合均值方差模型的極大似然估計的方法，同時給出調整參數ιn和λn的選擇方法．

3.1 計算組合懲罰之下的聯合均值與方差模型的極大似然估計

首先，注意到對數似然函數L(θ)的一、二階導數是連續的,對給定的θ0,對數似然函數近似為

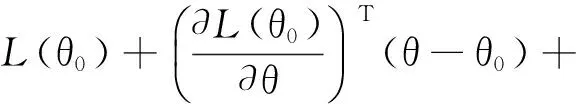
令組合懲罰部分為

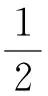
這里

J′λ·,ι·(|θ0j|)=ι·θ0j+P′λ·(|θ0j|)sgn(θ0j)

當下標“·”取1時,j=1,…,p；當下標“·”取2時,j=1,…,q．

因此，除了相差一個與參數無關的常數項外，組合懲罰似然函數式(3)便可二次逼近為

其中

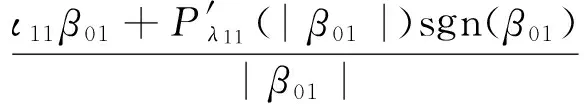
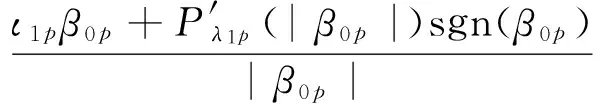
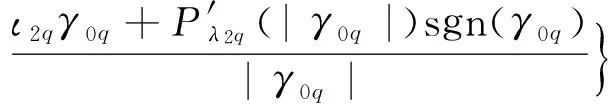
θ=(θ1θ2…θs)T= (β1β2…βpγ1γ2…γq)T

θ0=(θ01θ02…θ0s)T= (β01β02…β0pγ01γ02…γ0q)T

因此Q(θ)的二次最優化解可通過下列迭代得到:

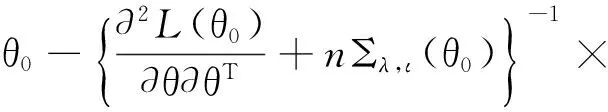
(4)

其次,在本文探討的模型下的對數似然函數L(θ)可寫為

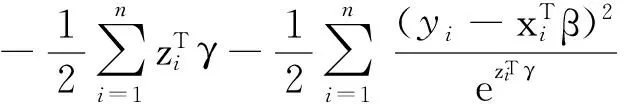
而且有

其中

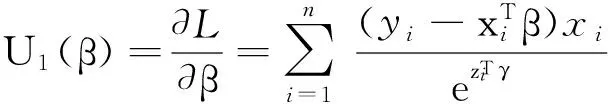
同樣地

其中

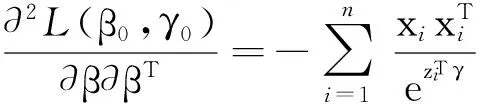
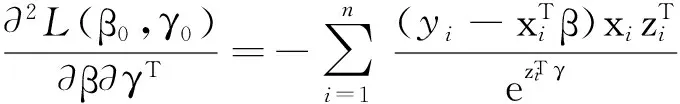
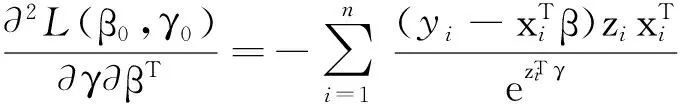
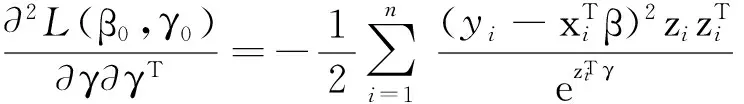
利用式(4),就可以找到聯合均值與方差模型在組合懲罰下的極大似然估計的迭代值．

3.2 調整參數ιn和λn的選擇

為了補充前面所介紹的方法,還需要對調整參數ιn和λn進行選擇．事實上,有很多選擇調整參數的工具,如CV、GCV、AIC及BIC等準則．

Wang等[11]提出BIC準則在模型選擇中具有相合性,利用該準則能依概率1選擇真實的模型．因此本文也采用BIC準則來選擇ιn和λn,定義如下:

4 模擬研究

對聯合均值與方差模型基于不同的樣本量和懲罰函數在兩種場景下的變量選擇方法進行比較研究．從下面的聯合均值與方差模型產生模擬數據:

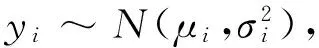
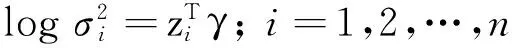
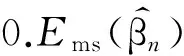
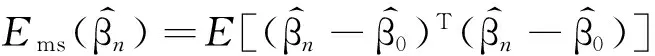
情景1xi取自于均值為0,協方差為r|i1-i2|的多元正態分布,且是pn=10維向量(i,i1,i2=1,2,…,n)．zj取自于均值為0,協方差為r|j1-j2|的多元正態分布,且是qn=15維向量(j,j1,j2=1,2,…,n)．分別取r=0.1,r=0.9．該情景下的模擬結果匯總于表1．

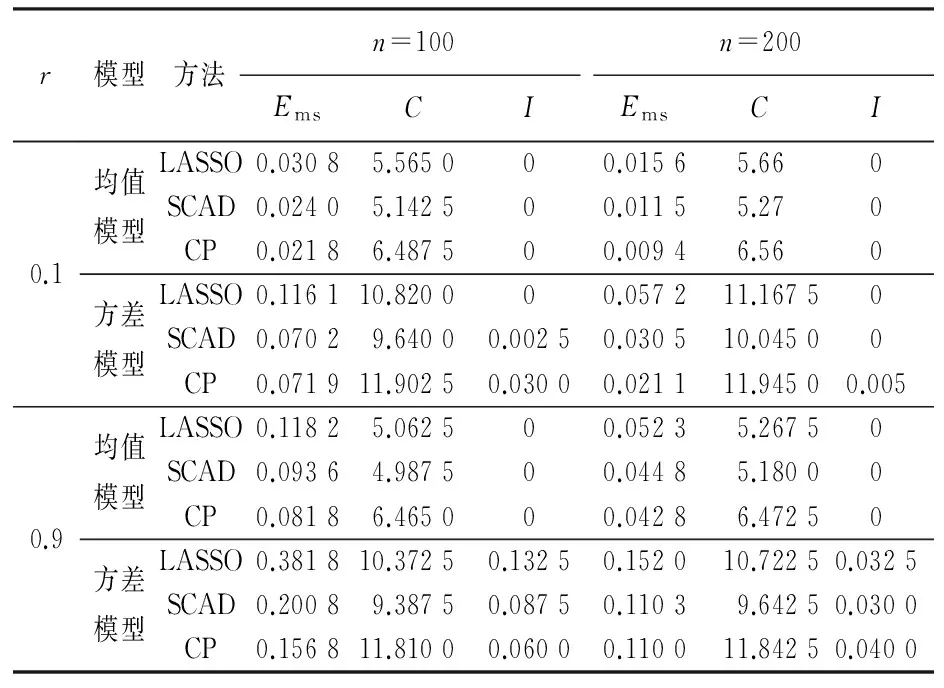
通過觀察表1的結果,可得到以下的結論:

(1)隨著樣本量n的增大,不論是均值模型還是方差模型的均方誤差Ems都在逐漸變小,同時C與I的選擇結果也越來越準確．

(2)相關性較高時,明顯顯示出了CP懲罰的優越性,說明了相關性較高的解釋變量在CP懲罰下的結果更加完美．

情景2xi(i=1,…,n)是pn=10維的獨立同分布的隨機變量,對于xi的前6維分量,xik～N(0,1)(k=1,…,6)．當k=7,…,10時,xik與和它強相關的變量xi,k-4有關,即xik用xi,k-4+ηk來代替,其中ηk是獨立同分布且服從N(0,0.01) 的分布．zj(j=1,…,n)是qn=15維的獨立同分布的隨機變量,對于zj的前9維分量,zjt～N(0,1)(t=1,…,9)．當t=10,…,15時,zjt=zj,t-6+ηt,其中ηt是獨立同分布且服從N(0,0.01) 的分布．該情景下的模擬結果匯總于表2．

表1 基于情景1之下的聯合均值與方差模型的變量選擇方法比較研究

Tab.1 The comparative study of variable selection via combined penalization in the joint mean and variance models in Scenario 1

r模型方法n=100n=200EmsCIEmsCI0.10.9均值模型LASSO0.03085.565000.01565.660SCAD0.02405.142500.01155.270CP0.02186.487500.00946.560方差模型LASSO0.116110.820000.057211.16750SCAD0.07029.64000.00250.030510.04500CP0.071911.90250.03000.021111.94500.005均值模型LASSO0.11825.062500.05235.26750SCAD0.09364.987500.04485.18000CP0.08186.465000.04286.47250方差模型LASSO0.381810.37250.13250.152010.72250.0325SCAD0.20089.38750.08750.11039.64250.0300CP0.156811.81000.06000.110011.84250.0400

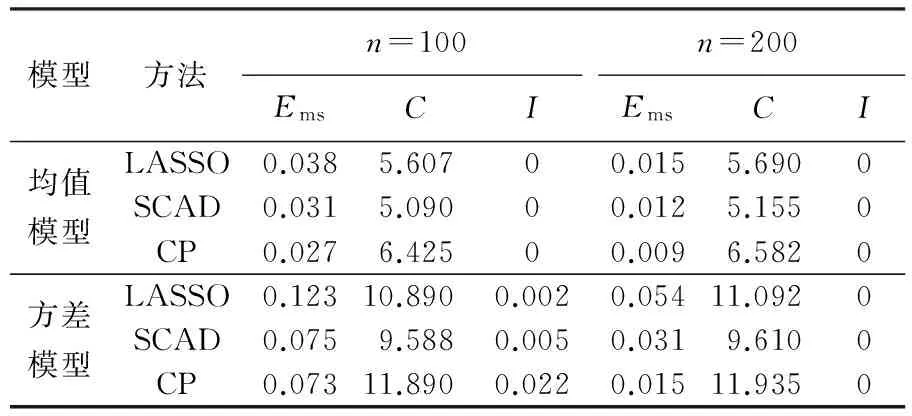
表2 基于情景2之下的聯合均值與方差模型的變量選擇方法比較研究

Tab.2 The comparative study of variable selection via combined penalization in the joint mean and variance models in Scenario 2

模型方法n=100n=200EmsCIEmsCI均值模型LASSO0.0385.60700.0155.6900SCAD0.0315.09000.0125.1550CP0.0276.42500.0096.5820方差模型LASSO0.12310.8900.0020.05411.0920SCAD0.0759.5880.0050.0319.6100CP0.07311.8900.0220.01511.9350

通過觀察表2的結果, 可得到以下的結論:

(1)隨著樣本量n的增大,不論是均值模型還是方差模型的均方誤差Ems都在逐漸變小,同時C的選擇結果也越來越準確．

(2)在該情景之下,解釋變量的生成本身就具有高度的相關關系,這里也明顯顯示出了CP懲罰對相關度較高的解釋變量的作用之大．

5 結 語

本文在聯合均值與方差建模的框架下,基于組合懲罰極大似然估計提出了一種變量選擇方法．與均值模型類似,方差模型可能依賴于許多感興趣的解釋變量,同時對均值模型與方差模型進行變量選擇可以避免建模的偏差和減少模型的復雜性是非常重要的．

本文運用CP組合懲罰將SCAD懲罰和嶺回歸混合在一起進行變量選擇．該懲罰充分利用了嶺回歸能克服解釋變量相關性過高對估計效果的影響,同時也證明了這樣的懲罰具有相合性和Oracle性質．隨機模擬的結果可以充分地說明該懲罰在給定模型下是十分有效的．今后可以試著將該模型推廣到更一般的情形,同時仍然可以利用CP組合懲罰來研究相關性較高的解釋變量的模型的變量選擇問題．

[1]FAN Jian-qing, LYU Jin-chi. A selective overview of variable selection in high dimensional feature space (invited review article) [J]. Statistica Sinica, 2010,20(1):101-148.

[2]Harvey A C. Estimating regression models with multiplicative heteroscedasticity [J]. Econometrica, 1976,44(3):461-465.

[3]Engel J, Huele A F. A generalized linear modeling approach to robust design [J]. Technometrics, 1996,38(4):365-373.

[4]Smyth G K, Verbyla A P. Adjusted likelihood methods for modelling dispersion in generalized linear models [J]. Environmetrics, 1999,10(6):695-709.[5]Lee Y, Nelder J A. Generalized linear models for the analysis of quality-improvement experiments [J]. Canadian Journal of Statistics, 1998,26(1):95-105.[6]WANG Da-rong, ZHANG Zhong-zhan. Variable selection in joint generalized linear models [J]. Chinese Journal of Applied Probability and Statistics, 2009,25(3):245-256.[7]吳劉倉,張忠占,徐登可. 聯合均值與方差模型的變量選擇[J]. 系統工程理論與實踐, 2012,32(8):1754-1760.

WU Liu-cang, ZHANG Zhong-zhan, XU Deng-ke. Variable selection in joint mean and variance models [J]. System Engineering — Theory & Practice, 2012,32(8):1754-1760. (in Chinese)

[8]黃 麗,吳劉倉. 基于對數正態分布下聯合均值與散度廣義線性模型的極大似然估計[J]. 高校應用數學學報:A輯, 2011,26(4):379-389.

HUANG Li, WU Liu-cang. Maximum likelihood estimator for joint mean and dispersion in generalized linear models of the Lognormal distribution [J]. Applied Mathematics a Journal of Chinese Universities:Ser. A, 2011,26(4):379-389. (in Chinese)[9]WANG Xiao-ming, Park T, Carriere K C. Variable selection via combined penalization for high-dimensional data analysis [J]. Computational Statistics and Data Analysis, 2010,54(10):2230-2243.[10]FAN Jian-qing, LI Run-ze. Variable selection via nonconcave penalized likelihood and its Oracle properties [J]. Journal of the American Statistical Association, 2001,96(456):1348-1360.

[11]WANG Han-sheng, LI Run-ze, Tsai C L. On the consistency of SCAD tuning parameter selector [J]. Biometrika, 2007,94(3):553-568.

Variableselectionviacombinedpenalizationinjointmeanandvariancemodels

DONG Ying1,2, SONG Li-xin*1, SHI Xin-yong1,3

( 1.School of Mathematical Sciences, Dalian University of Technology, Dalian 116024, China；2.College of Science, Dalian Nationalities University, Dalian 116600, China；3.Troops 68048, The Chinese People′s Liberation Army, Baoji 721013, China )

In the production and econometric area, controlling the variance of the quality of the product can guarantee the stable quality of products. So scholars are very interested in joint mean and variance models nowadays. In general, it is uncommon for explanatory variables to be uncorrelated. A combined penalization, which is mixed by the smoothly clipped absolute deviation (SCAD) penalty and ridge, is proposed. It can outperform the SCAD penalty technique when the correlation among predictors is high. At the same time, the consistency and the Oracle properties of the combined penalization are proved. Then, the combined penalization is used to select variables in joint mean and variance models. The results of stochastic simulation show that this model and method are effective.

combined penalization; joint mean and variance model; variable selection; penalized maximum likelihood

1000-8608(2014)01-0147-05

2013-04-01；

: 2013-11-28．

國家自然科學基金資助項目(61175041,11371077)；國家自然科學基金青年基金資助項目(11101062)；中央高校基本科研業務費專項資金資助項目(DUT12LK29)；大連民族學院自主科研基金資助項目(DC120101115).

董 瑩(1980-),女,博士生,E-mail:dongying@dlnu.edu.cn；宋立新*(1966-),男,教授,博士生導師,E-mail:lxsong@dlut.edu.cn.

O212

：A

10.7511/dllgxb201401022