基于FPGA和符號LMS算法的自適應濾波器設計*

邱陳輝,李　鋒,徐祖強

(1.浙江大學生物醫學工程教育部重點實驗室,杭州 310027;2.江蘇科技大學電子信息學院,江蘇 鎮江 212003)

?

基于FPGA和符號LMS算法的自適應濾波器設計*

邱陳輝1,李鋒2*,徐祖強2

(1.浙江大學生物醫學工程教育部重點實驗室,杭州 310027;2.江蘇科技大學電子信息學院,江蘇 鎮江 212003)

摘要:為了減少實現基于FPGA和LMS算法的自適應濾波器過多消耗硬件資源的問題,提出了符號LMS算法,通過降低乘法運算的次數來提高自適應濾波器的運行速度,并使用流水線技術進行優化。軟件仿真驗證了符號LMS算法的可行性,硬件仿真證實了采用該算法和流水線技術的自適應濾波器的優越性。

關鍵詞:數字信號處理;自適應濾波器;最小均方;符號最小均方;現場可編程門陣列;流水線

自適應濾波器在現代數字信號處理中的應用極為廣泛,主要分成系統辨識、逆模型、預測和干擾消除4大類別[1]。對于實時性要求很高的場合,往往需要使用硬件設計自適應濾波器,并且自適應算法盡量簡單、易實現[2]。基于現場可編程門陣列(FPGA)硬件和最小均方(LMS)自適應算法的自適應濾波器近年來被不斷地研究和改進。

由于FPGA中嵌入了較多硬線乘法器和加減器,使用它們很容易實現乘累加(MAC)運算,故通常將采用LMS算法的自適應濾波器直接映射到FPGA芯片上。但這樣消耗較多的硬件資源,也不能發揮FPGA并行處理的優勢。故本文提出了利用符號LMS算法和流水線技術對上述自適應濾波器進行優化,從而減少嵌入式乘法器資源的消耗并且提高運行速度。

1　自適應濾波器算法

1.1LMS算法

設x(n)和w(n)分別表示自適應濾波器的輸入信號和權值向量,定義

x(n)=[x(n),x(n-1),…,x(n-L+1)]T

w(n)=[w0(n),w1(n),…,wL-1(n)]T

則LMS算法的基本形式如下

濾波輸出:

(1)

誤差計算:

e(n)=d(n)-y(n)

(2)

權值更新:

w(n+1)=w(n)+μe(n)x(n)

(3)

其中y(n)是自適應濾波器的輸出信號,d(n)是期望信號,e(n)表示誤差信號,μ是收斂因子,L是自適應濾波器的階數。因為LMS算法是嚴格順序執行的,所以式(1)～式(3)的次序不能顛倒[3]。其模塊圖如圖1所示。

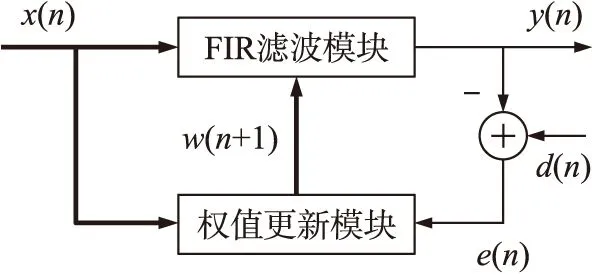
圖1　LMS算法的模塊圖

雖然LMS算法的推導過程涉及求梯度和微分,但是其最終形式只涉及乘法、加減和迭代3種運算,并且乘法運算量最多。而利用FPGA實現基于LMS算法的自適應濾波器時,硬件資源的消耗很大一部分來源于乘法運算。不管是利用FPGA中的基本邏輯單元LE(Logic Element)還是嵌入式乘法器模塊實現乘法運算,基于硬件的乘法運算都將是高成本的,應盡可能地減少[4]。

1.2符號LMS算法

式(1)中的乘法是為了計算自適應均衡器的輸出信號,不能刪減。式(3)中的乘法是針對收斂因子μ、誤差信號e(n)和輸入矢量x(n)進行的,可以進行改進。針對一些特殊應用,e(n)和x(n)的乘積事實上無需兩者都以全精度值參與計算,只取他們的符號進行運算即可[5]。

第1種方案是對e(n)取符號,利用正負號符號函數Signum(·)得 sign[e(n)],而x(n)保持全精度,這樣兩者相乘的結果就是x(n),要么是對x(n)取負值。第2種方案是對x(n)中的x(n)、x(n-1)、…、x(n-L+1)取符號,利用Signum(·)得sign[x(n)],此時兩者的乘積要么就是e(n),要么就是對e(n)取負值。第3種方案是同時對e(n)和x(n)取符號,利用Signum(·)得sign[e(n)]和sign[x(n)],這樣兩者相乘的結果就是1或-1。這3種符號LMS算法方案的公式表示依次為

w(n+1)=w(n)+μsign[e(n)]x(n)

(4)

w(n+1)=w(n)+μe(n)sign[x(n)]

(5)

w(n+1)=w(n)+μsign[e(n)]sign[x(n)]

(6)

符號LMS算法其實是對LMS算法的一種改進,其模塊圖如圖2所示,它可由隨機梯度法推導而來,以均方誤差E[|e(n)|2]為代價函數J(n),推導關鍵是對J(n)求梯度,然后對其權值w(n)進行自適應調整時,只考慮J(n)的梯度方向,忽略具體的梯度值。因此,犧牲輸入信號或誤差信號精度的符號LMS算法并不適用于所有的自適應系統[6],利用MATLAB對使用該算法的自適應濾波器進行前期的驗證評估是十分必要的。

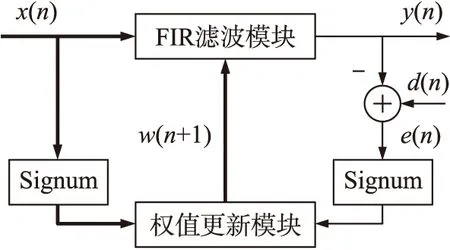
圖2　符號LMS算法的模塊圖

假若μ的取值不是2的冪形式,那么第1、第2種方案節省的乘法器數量相同,而第3種方案節省的乘法器數量是它們的2倍。若將μ值設置為2的冪形式,與μ相乘可以利用移位運算代替[7],那么上述3種方案所節省的乘法器數量是相同的。但是針對自適應濾波器的具體應用場合,3種方案對自適應濾波器的穩定性、收斂速度的影響會有差異。

由文獻[6]知第3種方案最受青睞,已被用作自適應差分脈沖編碼調制傳輸的國際電信聯盟標準,所以本文以它為例進行對比分析。圖3給出了分別基于LMS算法和符號LMS算法的自適濾波器的均方誤差曲線圖,這里取L=8,μ=2-7。由圖3可知采用符號LMS算法的自適應濾波器的均方誤差收斂速度比采用LMS算法更快,并且更加趨近于零。這主要由于在每次迭代更新中,符號LMS算法進行的乘法計算量相對于LMS算法減少了一半。

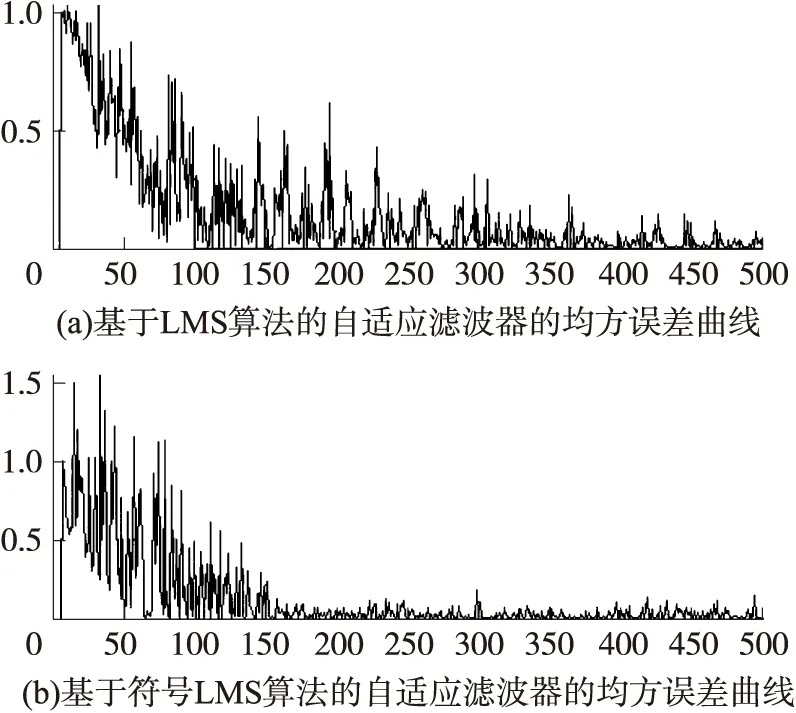
圖3　自適應濾波器的均方誤差曲線

2　流水線技術

廣義上講,流水線技術就是將一個重復的過程分解為若干子過程,讓每個子過程可以和其他的子過程同時進行,是一種并行處理技術。就FPGA而言,流水線技術是指將組合邏輯電路的延時路徑進行系統性地分級,并且在各個分級之間插入寄存器來暫存中間數據。這樣便縮短了信號在一個周期內通過組合邏輯電路的延時路徑長度,從而提高了時鐘頻率。對于應用最廣泛的同步時序電路而言,其處理速度就是指它的時鐘頻率。時鐘頻率越快,處理數據的時間間隔就越短,在單位時間內處理的數據量就越大,也就提高了處理速度[8]。

圖4形象說明了流水線技術的基本原理,假設圖中的組合邏輯電路具有較大的延時,于是將其分割成具有較小延時的組合邏輯電路1和2,并插入2個同步寄存器。這樣組合邏輯電路1和2在同一時間內處理的信號就會不同,因為經過了寄存器的鎖存。2個組合邏輯電路1和2就可以并行執行[9]。該圖也說明了流水線技術實際上是以增加硬件資源的消耗來換取更高處理速度的。

圖4　流水線技術基本原理圖

在FPGA中使用流水線技術,需要的額外成本不多,因為每個LE本身就包含一個寄存器和寄存器鏈邏輯。提升基于FPGA的自適應濾波器的運行速度關鍵在于提高乘法器的處理速度。由文獻[6]可知,對于FPGA中的一個N位×N位的乘法器,若想達到最高處理速度,那么需要的流水線級數是log2(N)。本文自適應濾波器輸入信號的位寬設置成16位,故采用4級流水線時可以充分發揮流水線技術的速度優勢。

3　FPGA實現

FPGA是通過采用可編程的查找表(LUT)結構來實現可編程邏輯的。LE是Cyclone系列FPGA芯片中最基本的可編程單元,主要由一個4輸入的LUT、一個可編程的寄存器、進位鏈邏輯和寄存器鏈邏輯構成[10]。因此,我們通常使用 在同一時鐘的驅動下 某信號通過源寄存器至目的寄存器的最短路徑所消耗的最少時間(Tmin或者Fmax)來表示對信號的處理速度,使用設計所需LE的總數量來表示FPGA硬件資源的消耗情況[11-12]。

為了跟本文1.2節最后的MATLAB仿真實驗保持一致,基于Altera公司CycloneⅢEP3C10U256C8FPGA芯片的自適應濾波器仍然設為8階,收斂因子仍取2-7,系統時鐘clk的頻率設成數據輸入頻率的6倍,自適應算法分別采用LMS算法和符號LMS算法。使用超高速集成電路硬件描述語言(VHDL)進行對分別基于2種算法的自適應濾波器進行編程,主要包括初始化模塊,信號輸入模塊,時鐘分頻模塊,權值更新模塊,誤差計算模塊,濾波輸出模塊。接著利用QuartusⅡ和ModelSim軟件對它們分別進行編譯、綜合、適配、時序分析。設定x(n)、d(n)、e(n)和y(n)的二進制位寬分別是16位,其中x(n)和d(n)的取值是通過對本文1.2節利用MATLAB仿真時的x(n)和d(n)數據進行16位量化得到的。

圖5是基于FPGA和LMS算法的自適應濾波器的ModelSim時序驗證圖,對該自適應濾波器進行VHDL編程時,沒有使用流水線技術進行優化,系統時鐘的最高頻率是76.75MHz,總共消耗了32個嵌入式乘法器。詳細的資源消耗情況如表1所示。圖5中誤差信號e的波形開始時抖動幅度較大,之后慢慢平緩,該設計達到了預期效果。

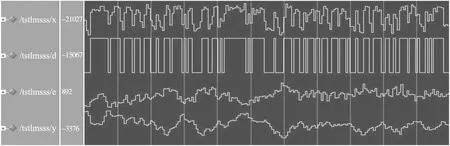
圖5　基于LMS算法的自適應濾波器的時序波形圖

圖6是基于FPGA和符號LMS算法的自適應濾波器的ModelSim時序驗證圖,在VHDL編程時添加了4級流水線對該自適應濾波器進行優化,圖6中誤差信號el的波形開始時抖動幅度很大,隨后漸趨平緩。和圖5中的e波形相比,圖6中el波形的抖動更小,這跟1.2節中的MATLAB仿真結果是完全一致的,因此本設計是正確的。表1也給出了該自適應濾波器的資源消耗情況和處理速度。

圖6　基于LMS算法的自適應濾波器的時序波形圖

表1基于2種算法的自適應濾波器的資源消耗和速度比較

算法LEsRegistersEmbeddedmultiplierFmax/MHzLMS141213213276．75符號LMS103793916123．93

由表1可知,基于LMS算法的自適應濾波器所消耗的LE和寄存器數量分別比基于符號LMS算法的多了375個和382個,并且前者所消耗的嵌入式乘法器數量是后者的2倍,但是前者的處理速度卻比后者慢很多。足見基于符號LMS算法的自適應濾波器在使用流水線技術優化后的優越性,并且這種優越性隨著自適應濾波器階數的升高、輸入位寬的增大將更加明顯。

事實上如果不使用流水線技術對基于符號LMS算法的自適應濾波器進行優化,那么它所消耗的LE和寄存器數量分別只有576個和412個,嵌入式乘法器的數量依然是16個,但此時自適應濾波器的處理速度明顯降低。這恰恰印證了本文第2節中流水線技術是以面積換取速度的論斷。

4　結束語

本文首先闡述了自適應濾波器常用的LMS算法和改進后的符號LMS算法,并且使用MATLAB作了前期對比分析,然后簡述流水線技術,最后將基于LMS算法和符號LMS算法的自適應濾波器在FPGA硬件上實現,并且使用流水線技術對基于符號LMS算法的自適應濾波器進行了優化。QuartusⅡ驗證得到了各種資源消耗情況和最高時鐘頻率,ModelSim仿真得到了基于2種算法的自適應濾波器的時序波形圖。將實驗數據進行對比分析,本文采用符號LMS算法和流水線技術的自適應濾波器在資源消耗和運行速度方面的確更具優勢。

參考文獻:

[1]Simon Haykin.自適應濾波器原理[M].鄭寶玉,譯.北京:電子工業出版社,2010:159-238.

[2]高亞軍.基于FPGA的數字信號處理[M].北京:電子工業出版社,2012:79-104.

[3]Bernard Widrow,Samuel D Stearns.自適應信號處理[M].王永德,龍憲惠,譯.北京:機械工業出版社,2008:68-76.

[4]吳高奎.數字信號處理算法的FPGA高速實現研究[D].成都:電子科技大學,2011:7-21.

[5]祝燕華,劉建業,賴際舟,等.FOG信號的變步長符號LMS自適應消噪方法[J].成都:光電工程.2008,35(11):122-127.

[6]Uwe Meyer-Baese.數字信號處理的FPGA實現[M].劉凌,譯.北京:清華大學出版社,2011:425-468.

[7]Rui Guo,DeBrunner L S.A Novel Adaptive Filter Implementation Scheme Using Distributed Arithmetic[J].IEEE Signals,Systems and Computers,2011(11):160-164.

[8]Pramod Kumar Meher,Sang Yoon Park.High Throughput Pipelined Realization of Adaptive FIR Filter Based on Distributed Arithmetic[J].IEEE Transactions on VLSI and System-on-Chip,2013,60(6):346-350.

[9]潘松,黃繼業,潘明.EDA技術實用教程-Verilog HDL[M].北京:科學出版社,2010:232-236.

[10]楊海鋼,孫嘉斌,王慰.FPGA器件設計技術發展綜述[J].北京:電子與信息學報,2010(3):714-723.

[11]張春生,蘇開友.FPGA數字信號處理與工程應用實踐[M].北京:中國鐵道出版社,2013:149-156.

[12]Stephen Brown,Zvonko Vranesic.數字邏輯基礎與VHDL設計[M].伍微,譯.北京:清華大學出版社,2011:230-248.

邱陳輝(1988-)男,漢族,江蘇南通人,博士研究生,研究方向為基于FPGA的數字信號處理生物醫學信號處理,qch19881114@126.com;

李鋒(1970-)男,漢族,陜西商洛人,博士,副教授,碩士生導師,研究方向為光電信息處理,lifengsl@126.com;

徐祖強(1988-)男,漢族,江西贛州人,碩士研究生,研究方向為數字信號處理及其FPGA實現,930233502@qq.com。

DesignofAdaptiveFilterBasedonFPGAandSignum-LMSAlgorithm*

QIUChenhui1,LIFeng2*,XUZuqiang2

(1.The Key Lab of Biomedical Engineering of Ministry of Education,Zhejiang University,Hangzhou 310027,China;2.College of Electronics and Information,Jiangsu University of Science and Technology,Zhenjiang Jiangsu 212003,China)

Abstract:To decrease the consumption of hardware resource of adaptive filter based on FPGA and LMS algorithm,signum-LMS algorithm is proposed.The processing speed of adaptive filter is increased by reducing the number of multiplications and optimized by pipelining technology.Software simulation verifies the feasibility of signum-LMS algorithm.Hardware simulation proves the superiorities of the adaptive filter using the proposed algorithm and pipelining technology.

Key words:digital signal processing;adaptive filter;least mean square(LMS);signum-least mean square(SLMS);field programmable gate array(FPGA);pipelining

doi:EEACC:127010.3969/j.issn.1005-9490.2014.05.023

中圖分類號:TN911.72

文獻標識碼:A

文章編號:1005-9490(2014)05-0904-04

收稿日期:2013-10-20修改日期:2013-11-13

項目來源:國家自然科學基金項目(11204109);國家自然科學基金項目(51307074)