大件運輸中簡支梁橋的動力響應分析及監測

劉波，王有志，王濤，叢侃，徐永芝

(1.山東大學 土建與水利學院，山東 濟南250061;2.長安大學 公路學院，陜西 西安710064)

中國加入WTO以來，公路大件運輸日趨頻繁，經由公路運輸的重型工業設備(如發電機靜子、變壓器及反應器等)重量不斷刷新記錄。繁重的大件運輸任務，對公路橋梁的承載能力和安全評估提出了挑戰。目前針對超重大件過橋的研究多集中于橋梁的承載能力評估、臨時加固措施方面［1-3］，針對大件過橋時車橋耦合振動響應的研究則較少。

大件運輸時一般需要對車輛所經過的橋梁進行臨時加固或補強，基于經濟性考慮遴選的運輸路線上鮮有大跨徑橋梁，往往中小跨徑橋梁占絕大多數。大件過橋時往往需要暫時中斷交通，禁止其余車輛、行人通過，為降低橋梁的動力響應要求大件運輸車輛以低速過橋。實際上，以“重車輕橋”、“長車短橋”為特征的大件運輸車橋耦合系統有其獨特的動力特性，一味地要求運輸車輛降低速度過橋往往并不現實，在很多情況下也沒有必要。

通過對車橋耦合系統的分析，本文把車橋系統分解成2個獨立的運動體系，即橋梁振動子系統和車輛振動子系統，利用車輪和橋面的位移協調方程來考慮車橋的接觸［4］。同時，以九龍河中橋為工程實例，利用ANSYS中APDL語言編寫車橋耦合振動分析程序，采用梁格法建立初始有限元模型。結合大件過橋時橋梁的動力響應監測數據，對車橋耦合系統的剛度、阻尼等參數進行反演，并對大件過橋時橋梁的動力學特性進行了分析和研究。

1 車橋耦合體系振動模型

研究車橋系統動力相互作用的經典方法有勻速移動常量力模型、勻速移動簡諧力模型、勻速滾動質量模型、勻速移動彈簧-質量模型等，在簡支梁強迫振動微分方程的基礎上，利用振型疊加法和振型的正交性推導出車橋系統的動力平衡方程。實際上，車輛由剛性底盤(車身)、懸架、輪胎等元件組成，各元件在空間具有浮沉、伸縮、側滑、俯仰、橫擺、側傾6個自由度(3個平動和3個轉動)，它們之間通過線性或非線性的各種阻尼器和彈簧元件連接。現代車橋耦合振動研究將汽車懸架、輪胎模擬為線性彈簧和阻尼器，考慮剛性車身的浮沉、伸縮、側滑、俯仰、橫擺、側傾6個自由度，研究車橋的豎向、橫向耦合振動［5］。本文針對斜橋結構的特性，建立空間整車模型，應用廣義虛功原理和有限元法推導了車輛振動子系統和橋梁振動子系統的振動方程組，然后通過位移協調方程來實現求解。

1.1 空間整體車輛模型

威海化工機械廠制造的土庫曼斯坦化工廠吸收塔每臺凈重488.1 t，選用4軸式牽引車+3縱25軸平板掛車+助力車運輸，裝載后平板掛車總重600.6 t，如圖1、2所示。車輛之間采用拖曳式聯接裝置，其主要承受縱向荷載，豎向荷載僅為聯接裝置的自重，由于主要關注車橋耦合系統的豎向振動，牽引車、平板掛車、助力車作為獨立車輛考慮。

由于車輛豎向與橫向振動之間的耦合效應較弱，為計算簡便，將車輛豎向與橫向振動分開進行，只考慮車體、懸架與輪胎的浮沉、俯仰自由度。簡化為二系的彈簧-質量-阻尼系統空間整體車輛模型如圖3所示，4軸牽引車包含8個端點11個自由度，3縱25軸平板掛車包含75個端點78個自由度，3軸助力車包含6個端點9個自由度。圖中:M為車體質量，3個自由度分別為豎向位移Z0、繞橫軸的旋轉自由度θ和繞縱軸的旋轉自由度φ;mi為構架質量與輪對質量之和，每個塊質量被賦予了1個豎向位移自由度Zi;Kui為二系豎向剛度;Cui為二系豎向阻尼;Kdi為一系豎向剛度;Cdi為一系豎向阻尼;i=1，2，…，N;對于牽引車輛，N=8，對于平板掛車，N=75，對于助力車，N=6;L、L1～L4表示車輛各軸及質心之間的縱向距離，B表示車體外側輪對間的橫向距離。

圖1 大件運輸夜間過橋Fig.1 oversize transport during night

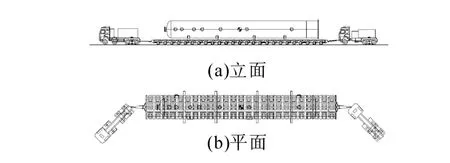
圖2 大件運輸車輛荷載簡圖Fig.2 Vehicle load for oversize transport

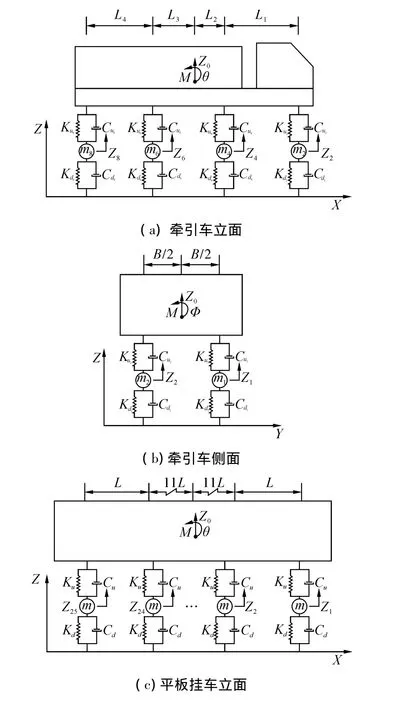
圖3 車輛簡化模型Fig.3 Simplified vehicle model

以車輛靜力平衡位置為起始點，在俯仰角θ和側傾角φ較小的情況下，車身第N個端點豎向位移方程為

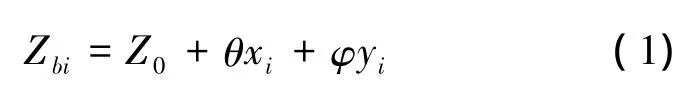
由廣義虛功原理［6］得

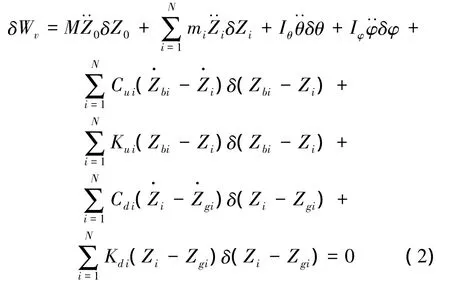
式中:δZ0、δZi、δθ、δφ 為車輛廣義虛位移，不為零;δZgi為橋梁廣義虛位移，相對車輛而言假設為零。

將式(1)代入式(2)，令廣義虛位移對應系數項為零，可得到如下方程:

車身質心豎向運動方程:

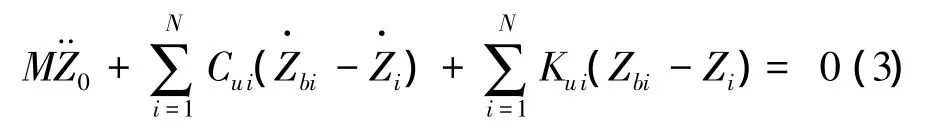
車身俯仰運動方程:

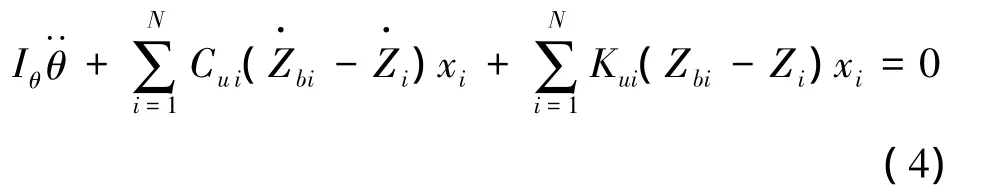
車身側傾運動方程:

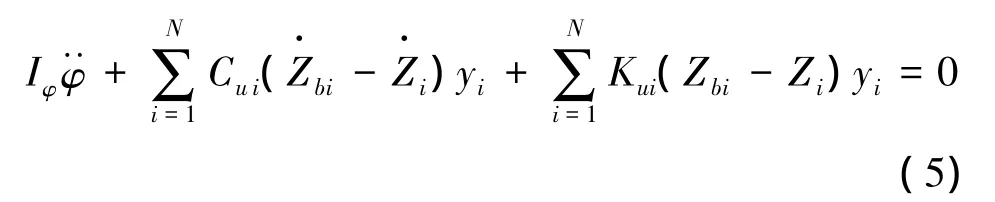
車輪豎向運動方程:

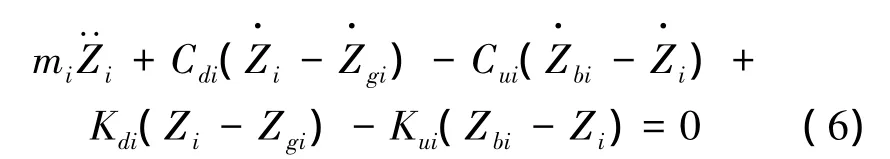
式中:xi、yi表示車輪的平面坐標。

將上述各式整理寫成矩陣形式得

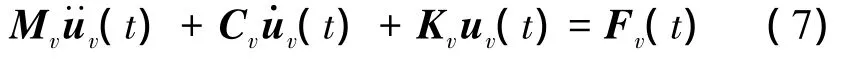
式中:Mv、Cv、Kv分別表示車輛振動系統的質量矩陣、阻尼矩陣和剛度矩陣，Fv(t)表示激振力列向量，(t)、(t)、uv(t)分別表示車輛振動系統的加速度、速度、位移列向量。

1.2 橋梁振動方程

采用梁格法建立空間有限元模型，橋梁結構的運動方程為

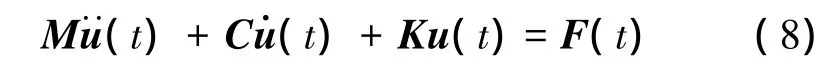
1.3 車橋耦合系統的位移協調條件

假設車輪在運行的過程中始終與橋面密貼不脫離，即得車橋耦合振動系統的位移協調條件如下

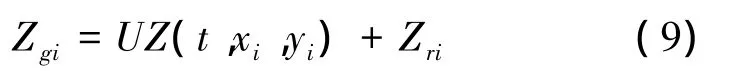
式中:UZ(t，xi，yi)表示車輪i對應橋梁節點的撓度，向下為負;Zri表示橋面上點的不平整度，向下為負。

根據車輛與橋梁接觸點間相互作用力的平衡關系，可得第i個車輪對橋梁結構的作用力如下

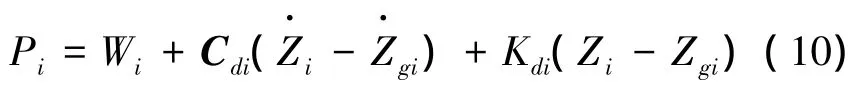
式中:Wi表示車輛靜止時車體分配到第i個車輪的重力與該輪自重之和，向下為負。

1.4 車橋耦合振動數值求解

車橋耦合系統振動方程為二階變系數微分方程組，荷載項均為時變函數，解此類方程大多采用直接積分法。本文采用Newmark-β隱式積分法進行數值求解，步驟如下:

1)建立橋梁模型，形成橋梁子系統質量矩陣、剛度矩陣、阻尼矩陣;

2)輸入車輛參數，形成車輛子系統質量矩陣、剛度矩陣、阻尼矩陣;

3)假定車橋耦合振動系統的初始狀態;

4)根據橋梁子系統的位移、速度及橋面不平整度確定橋梁子系統對車輛子系統的反作用力，形成式(7)荷載向量;

5)利用Newmark-β數值迭代法求解車輛子系統振動微分方程組，求出車輛子系統位移向量、速度向量、加速度向量;

6)計算車輛子系統對橋梁子系統的作用力，求解橋梁子系統振動微分方程組;

7)判斷平衡迭代收斂情況，若滿足收斂條件，則停止迭代。

2 實測橋面不平度與功率譜估計

橋面不平順是車橋耦合振動的主要激勵因素之一，按照功率譜密度可將路面不平度分為A～H共8級。為定量評價橋面不平度對車橋耦合系統動力響應的影響，需對實測橋面不平度進行功率譜估計和平度分級。傳統的功率譜估計方法通常直接或間接對有限個樣本數據進行傅里葉變換得到功率譜，其存在分辨率低、方差性能不好等缺點。基于AR模型的現代功率譜估計可以通過求解線性方程組得到模型參數的精確估計，進而可以求得精確的功率譜估計。

圖4所示為九龍河中橋實測的橋面不平度，采樣間距為30 cm，圖5為利用AR模型求解得到的橋面不平度功率譜，實測樣本的功率譜位于路面平度分級B區。

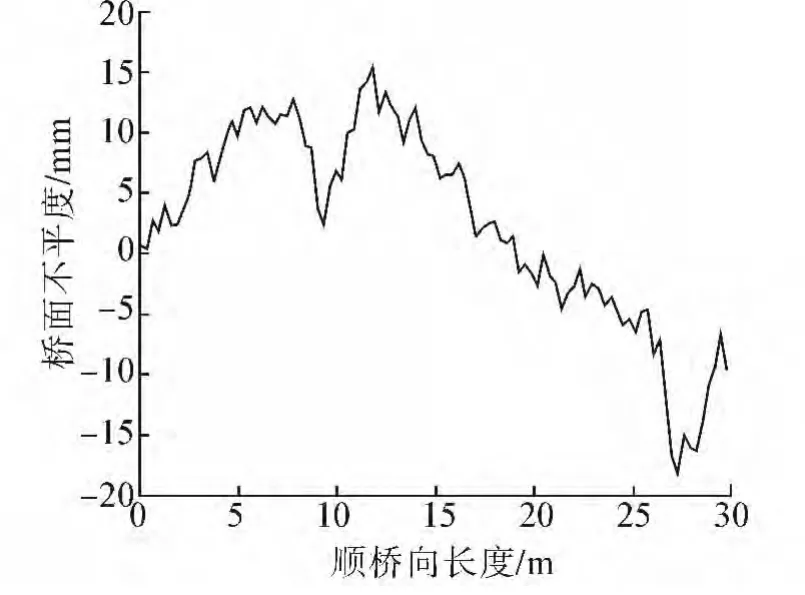
圖4 實測橋面不平度Fig.4 Measured deck roughness

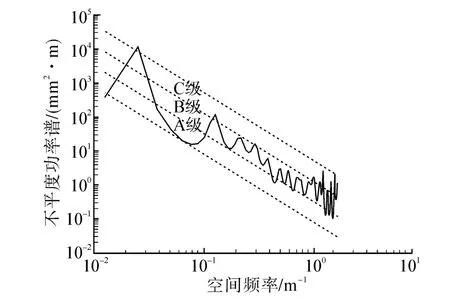
圖5 實測橋面不平度功率譜Fig.5 Measured deck roughness power spectrum

3 車橋耦合振動參數反演

車橋耦合振動分析面臨的一個主要問題是車橋振動系統的參數難以確定，而正分析的復雜性使得傳統反分析方法面臨著很大的挑戰，而基于改進的支持向量回歸機v-SVR的反分析方法能夠在少而精的正分析基礎上結合實測數據快速反饋出數值計算參數，是目前工程反分析研究領域一個很重要的研究方向［7］。

3.1 v-SVR 算法原理

回歸問題即尋找從輸入空間到輸出空間的一個映射f:Rn→Rl，使得f(x)=y。v-SVR的目標是尋求回歸函數［8］:

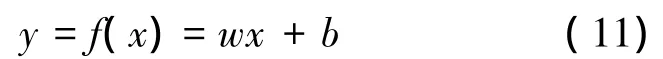
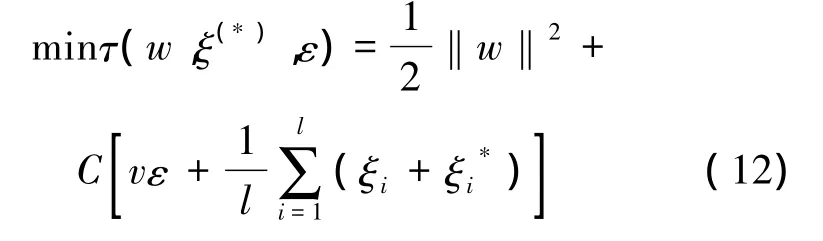
式中:C為用來平衡模型復雜性項和訓練誤差項的權重系數，ε為不敏感損失函數，ξ、ξ*為松弛因子。式(12)的對偶形式為

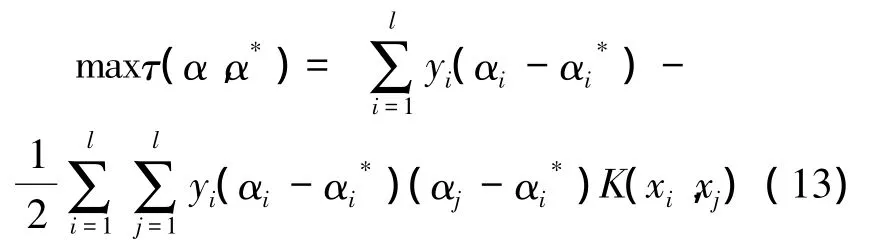
通過求解式(12)、(13)，即可得到通過學習訓練得到的回歸函數為

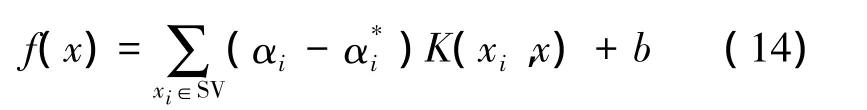
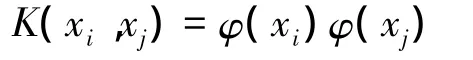
式中:αi為拉格朗日系數;SV為支持向量的集合為核函數，常用的有P階多項式、高斯徑向基核、多層感知器sigmoid核和樣條核函數等。

3.2 預測回歸模型的建立及參數反演

在對九龍河中橋撓度監測的基礎上，建立反分析目標函數如下:

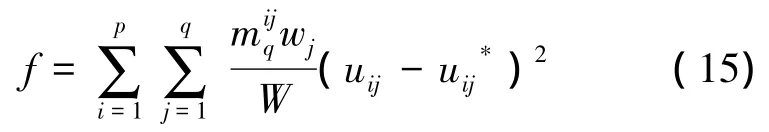
式中:uij表示第i塊板實測撓度時程曲線第j個特征點的撓度，表示uij對應的理論計算值，表示車輛荷載的橫向分布系數，wj表示第j個特征點對應主要車輛的重量，W表示車隊的總重。

通過對車橋耦合振動問題的分析，確定車橋系統待反演13個參數的取值范圍，確認反演構造樣本如表1所示。同時，采用正交設計表L27(313)給出訓練的學習樣本，對于每一種試驗組合，ANSYS進行正向計算，找出對應的監測點豎向位移值，根據式(15)計算目標函數值，將與其對應的待反演參數組合成一個學習樣本，共得到27個訓練樣本。

參數回歸反演首先要根據訓練樣本建立回歸預測模型［9］，本文采用留一法設計預測模型，采用網格搜索法搜索最優計算參數。最優參數對應的支持向量機即為可用于反分析的關于待反演參數與監測位移的表面響應模型。通過適當擴大待反演參數的搜索范圍和密度，令目標函數取極小值得到13個參數的反演結果如表2所示。

表1 反演樣本構造Table l Constructed samples for back-analysis

表2 參數反演結果Table 2 Parameter from back-analysis

4 動力響應分析

4.1 跨中撓度理論與實測結果對比

九龍河中橋寬40 m，跨徑布置為5 m×10 m，斜交角67°，上部結構為簡支空心板。大件過橋時嚴格按照劃定的車道低速(6.2 km/h)均勻行駛，采用DEWE-3010多通道動態數據采集系統和機電百分表監控首跨空心板的跨中撓度，測點編號1～7，如圖6所示，其中P表示軸重。在車橋耦合振動參數反演的基礎上，將表2中的參數代入正分析程序可得跨中撓度的理論和實測時程對比曲線如圖7所示。

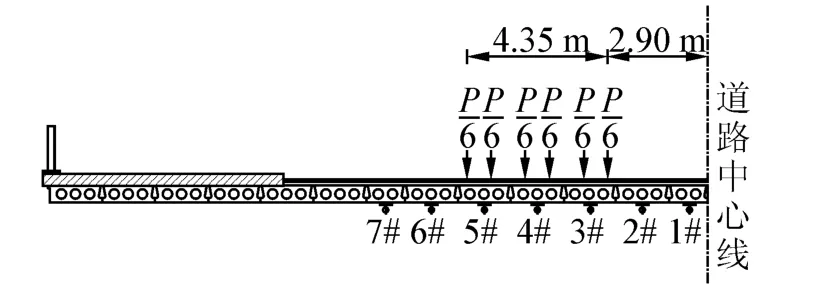
圖6 動撓度測點橫向布置示意圖Fig.6 Transverse arrangement of measuring points

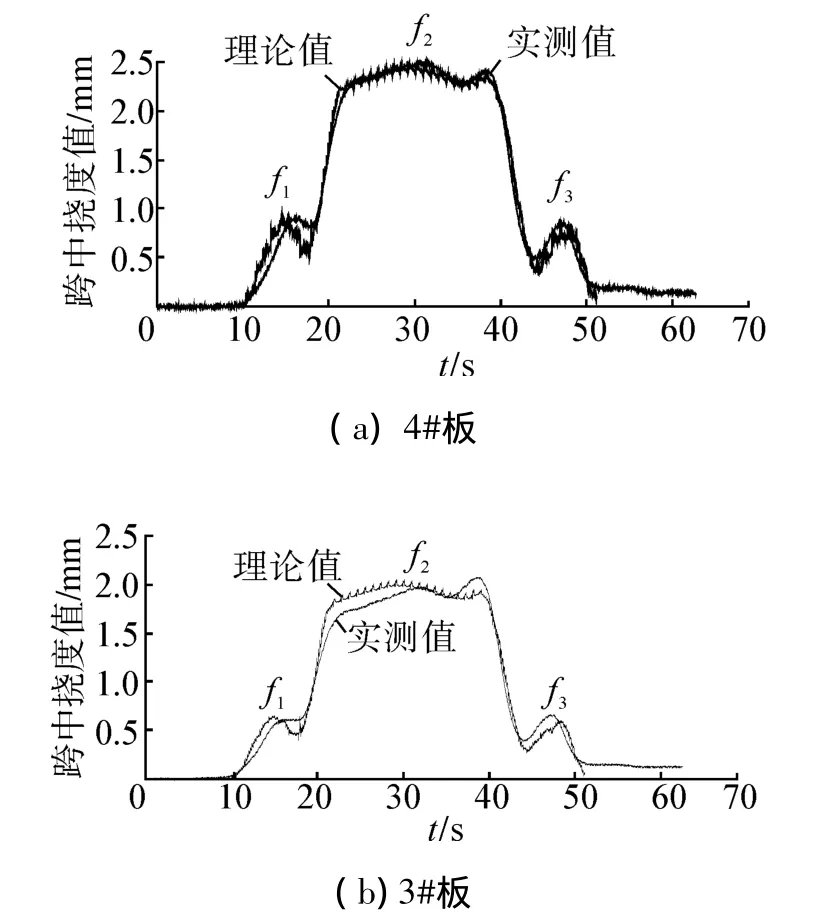
圖7 跨中撓度理論和實測時程曲線圖Fig.7 Theoretical and measured deflection time-history curve

從圖7可以看出，跨中撓度的理論計算值和實測值基本吻合。4#板受力最大，跨中最大撓度理論值為2.515 mm，與實測值 2.525 mm 相差約 0.4%;利用v-SVR預測回歸模型得到的跨中最大撓度預測值為2.584 mm，與實測值相差約2.3%。圖7撓度時程曲線出現3個大的波峰f1、f2、f3，f1表示牽引車引起的跨中撓度極值;f2呈平臺狀，表示平板掛車車輪持續滿跨布置時引起的跨中撓度峰值區間;f3表示助力車引起的跨中撓度極值。撓度時程曲線f2平臺相對比較平穩，但是也存在明顯的波動，這主要是由于橋面不平度引起的，不同的橋面不平度產生不同的波形。

4.2 速度和加速度

圖8表示跨中截面豎向速度、加速度時程曲線，由圖中可以看出，對應于撓度曲線平臺段的空心板跨中截面豎向速度和加速度受到明顯抑制，曲線呈“啞鈴型”，這是由于平板掛車車輪持續滿跨布置所引起的，這也是“長車短橋”車橋耦合振動系統的顯著特征。當掛車長度大于橋梁跨度時，平板掛車對橋梁來說既是荷載又是約束，兩者耦合振動作用明顯。

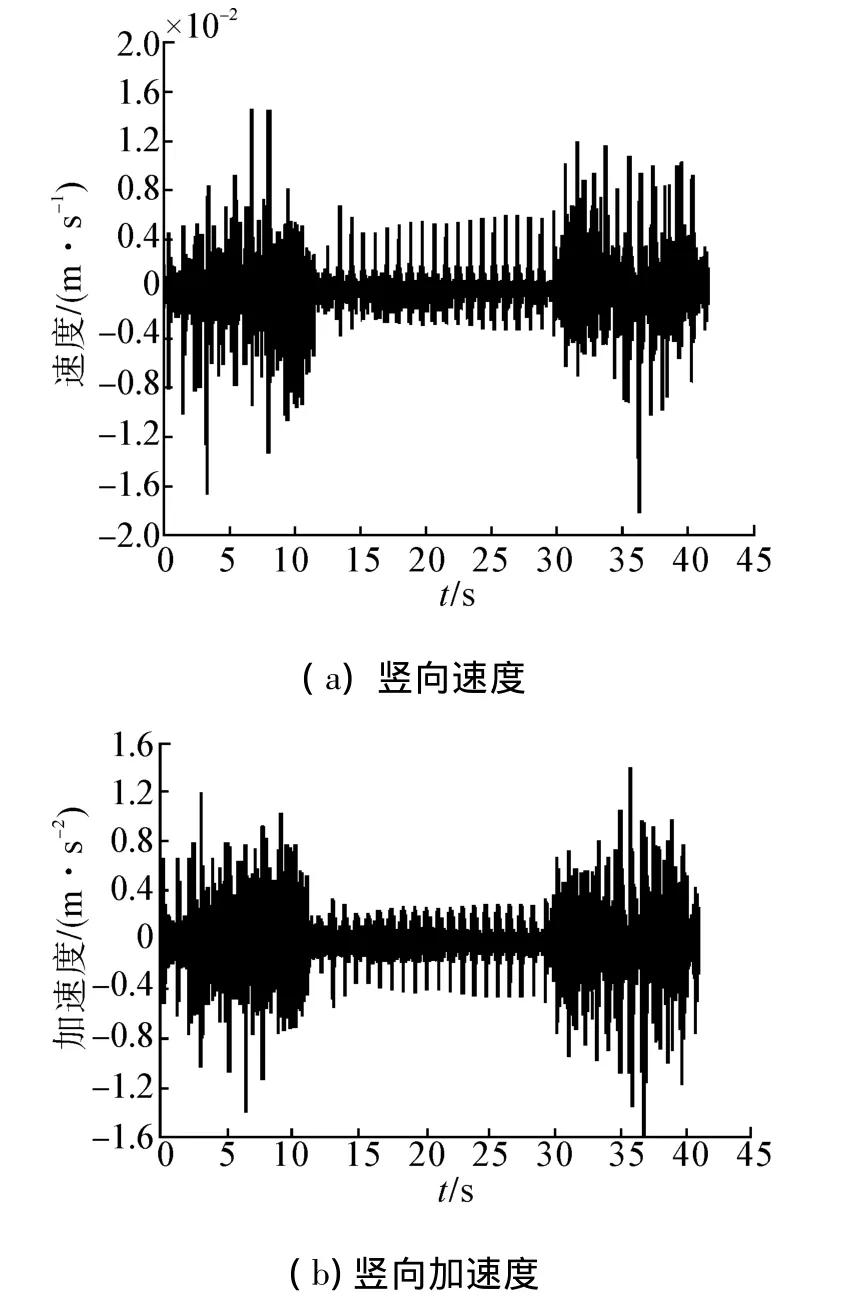
圖8 跨中截面動力響應時程曲線Fig.8 Time-history curve of dynamic response

4.3 沖擊系數

行駛在公路橋梁上的汽車車輛因受到多種復雜因素的影響，對橋梁產生的動力效應往往會大于其靜止作用在橋上所產生的靜力效應，稱之為車輛的沖擊效應。車輛的沖擊效應一般用沖擊系數定義如下:

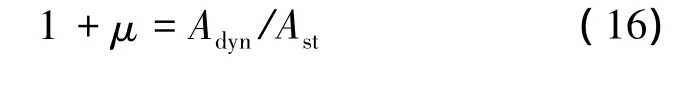
式中:Adyn為車輛荷載過橋時橋梁跨中動態撓度的峰值;Ast為同一車輛荷載靜力作用時跨中撓度的最大值。目前我國規范在橋梁結構的沖擊系數計算中僅僅考慮了結構的基頻。實際上沖擊系數不僅與結構的基頻有關，還與橋面不平度、車輛行駛速度、車輛自身各部分之間的連接剛度和阻尼等參數密切相關。

根據式(16)，當大件運輸車輛以6.2 km/h的低速度過橋時，沖擊系數實測值為0.119，雖然低于文獻［10］計算值 0.388(基頻為 9.83 Hz)，但是仍然不可忽視。這打破了以往的認識，意味著在進行大件過橋承載力評估時即使運輸車輛以低速過橋也必須考慮車輛荷載的沖擊效應。

在實測橋面不平度激勵下，對不同車速下 (5～40 km/h)橋梁的動力響應進行計算后發現，沖擊系數的變化范圍為0.118～0.124，車速對沖擊系數的影響較小。

我國的道路路面不平度基本屬于A～C級，將路面功率譜進行快速傅里葉逆變換［11］即可重構路面不平度樣本。圖9為B級路面不平度重構樣本，圖10表示不同路面等級、不同車速下的沖擊系數。可以看出，車速的變化對沖擊系數的影響同樣較小且并無明確的變化規律［12］，而路面不平度對沖擊系數的影響較大。路面極平時可以不考慮車輛的沖擊系數，A～C級路面的沖擊系數分別為 0.041～0.064、0.105～0.126、0.221～0.254。

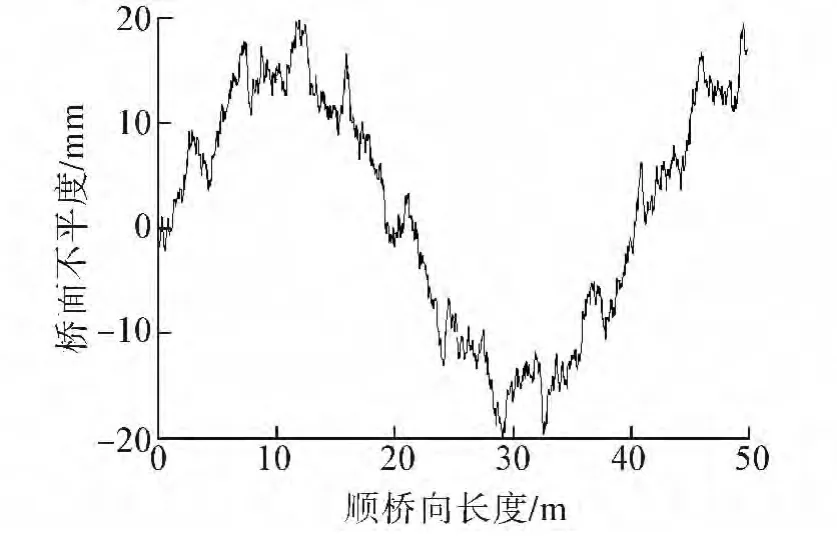
圖9 B級路面不平度Fig.9 Class B road roughness

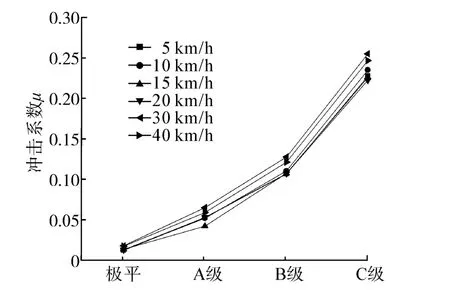
圖10 不同路面等級、不同車速下的沖擊系數Fig.10 Impact factor under different road roughness and speed

5 結論

1)對大件運輸時橋梁結構的動力響應進行了理論分析和實橋監測，理論值和實測值吻合較好。

2)外運大件以6.2 km/h的低速通過橋面不平度為B級的簡支梁橋時，其實測沖擊系數仍然達到0.119。在對大件過橋進行安全評估時，即使運輸車輛以低速通過，也應考慮車輛荷載的沖擊作用。

3)大件過橋時，對于中小跨徑橋梁，車速對于沖擊系數的影響較小，路面不平度對于沖擊系數的影響較大。在滿足交通安全的前提下，不應過度限制運輸車輛的速度，對橋面進行平整度處理是降低車輛沖擊效應的有效方法。

4)撓度時程曲線峰值平臺、“啞鈴型”的速度和加速度時程曲線為“長車短橋”耦合振動系統的顯著特征，平板掛車對橋梁來說既是荷載又是約束，兩者耦合振動作用明顯。

5)正交試驗和支持向量回歸機v-SVR的結合顯著提高了參數反演的效率，基于v-SVR預測模型的精度能夠滿足工程需要。

［1］邢文榜.大件運輸中橋梁通過性快速評定方法研究［J］.中外公路，2011，31(3):217-220.XING Wenbang.Rapid assessment method research on bridge during oversize transport［J］.Journal of China ＆ Foreign Highway，2011，31(3):217-220.

［2］劉堯，葉貴如，張治成.橋上橋在大件運輸中的應用研究［J］.武漢理工大學學報:交通科學與工程版，2008，32(1):176-179.LIU Yao，YE Guiru，ZHANG Zhicheng.Method"bridge on the bridge"used in the massive product transportantion［J］.Journal of Wuhan University of Technology:Transportation Science＆ Engineering，2008，32(1):176-179.

［3］錢鴻，蒙云，張會禮，等.大件運輸中橋上橋的特殊用法與工程實踐［J］.重慶交通學院學報，2005，24(5):10-13.QIAN Hong，MENG Yun，ZHANG Huili，et al.A special application of temporary steel bridge in heavy-cargo transportation［J］.Journal of Chongqing Jiaotong University，2005，24(5):10-13.

［4］施穎，宋一凡，孫慧，等.基于ANSYS的公路復雜橋梁車橋耦合動力分析方法［J］.天津大學學報，2010，43(6):537-543.SHI Ying，SONG Yifan，SUN Hui，et al.Dynamic analysis method of vehicle-bridge coupling for complicated bridges based on ANSYS［J］.Journal of Tianjin University，2010，43(6):537-543.

［5］李小珍，張黎明，張潔.公路橋梁與車輛耦合振動研究現狀與發展趨勢［J］.工程力學，2008，25(3):230-240.LI Xiaozhen，ZHANG Liming，ZHANG Jie.State-of-the-art review and trend of studies on coupling vibration for vehicle and highway bridge system［J］.Engineering Mechanics，2008，25(3):230-240.

［6］曾慶元.彈性系統動力學總勢能不變值原理［J］.華中理工大學學報，2000，28(1):1-3.ZENG Qingyuan.The principle of total potential energy with stationary value in elastic system dynamics［J］.Journal of Huazhong University of Science and Technology，2000，28(1):1-3.

［7］邢萬波，周鐘，唐忠敏，等.基于v-SVR和改進PSO算法的反分析方法及應用［J］.巖土力學，2009，30(增 2):540-546.XING Wangbo，ZHOU Zhong，TANG Zhongmin，et al.A new back-analysis method based on ν-SVR and improved PSO algorithm and its application［J］.Rock and Soil Mechanics，2009，30(Suppl 2):540-546.

［8］SCHOLKOPF B，SMOLA A，WILLIAMSON R，et a1.New support vector algorithms［J］.Neural Computation，2000(12):1207-1245.

［9］CHANG C C，LIN C J.LIBSVM:A library for support vector machine［R］.Taiwan:National Taiwan University，2001:5.

［10］JTG D60—2004.公路橋涵設計通用規范［S］.北京:人民交通出版社，2004:26.

［11］劉獻棟，鄧志黨，高峰.基于逆變換的路面不平度仿真研究［J］.中國公路學報，2005，18(1):122-126.LIU Xiandong，DENG Zhidang，GAO Feng.Study of simulation of road roughness based on inverse transform［J］.China Journal of Highway and Transport，2005，18(1):122-126.

［12］譚國金，劉寒冰，程永春，等.基于車-橋耦合振動的簡支梁橋沖擊效應［J］.吉林大學學報:工學版，2011，41(1):62-67.TAN Guojin，LIU Hanbing，CHENG Yongchun，et al.Analysis of impact of vehicle to simply supported beam［J］.Journal of Jilin University:Engineering and Technology Edition，2011，41(1):62-67.