錐 b-Banach空間的不動點(diǎn)定理

鮑寶國，盧冬暉

(湖北師范學(xué)院 數(shù)學(xué)與統(tǒng)計學(xué)院， 湖北 黃石 435002)

錐 b-Banach空間的不動點(diǎn)定理

鮑寶國，盧冬暉

(湖北師范學(xué)院 數(shù)學(xué)與統(tǒng)計學(xué)院， 湖北 黃石 435002)

通過新定義錐b-Banach 空間的概念，推廣了錐Banach 空間的概念，并推廣了Karapinar的兩個不動點(diǎn)定理。

錐Banach 空間;錐 b-Banach空間;不動點(diǎn)

在2007年，黃龍光和張憲[1]通過用借助錐而定義的半序來代替實(shí)數(shù)之間的半序定義出錐度量空間的概念，之后，很多建立在錐度量空間的不動點(diǎn)定理被發(fā)表出來[2，3]。Hussain N和Shah M H[4]在2011年又在錐度量空間的基礎(chǔ)之上，提出了錐b-度量空間，它討論的范圍比錐度量空間更大。最近，一個與錐度量空間緊密相關(guān)的錐Banach空間[5]被定義出來，Karapinar[6]把一些著名的度量空間的不動點(diǎn)定理推廣到這個空間。

在本文中，作者通過新定義錐b-Banach 空間的概念，推廣了錐 Banach空間的概念，而且推廣了Karapinar[6]的兩個不動點(diǎn)定理。

首先我們需要了解下面的定義。

定義1[1]設(shè)X是一個非空集合，d:X×X→E,滿足下列條件：

1)d(x,y)≥θ(?x,y∈X),d(x,y)=θ?x=y;

2)d(x,y)=d(y,x);

3)d(x,y)≤d(x,z)+d(z,y)(?x,y,z∈X)

稱d為X上的一個錐距離或錐度量，同時稱(X,d) 為錐度量空間或錐距離空間.

定義2[5]設(shè)X是一個向量空間，映射 ‖·‖c:X→E滿足：

1)‖x‖c≥θ(?x∈X),‖x‖c=θ?x=θ;

2)‖x+y‖c≤‖x‖c+‖y‖c(?x,y∈X);

3)‖kx‖c=|k|‖x‖c(?k∈,?x∈X)

稱 ‖·‖c為X上的一個錐范數(shù)，同時稱 (X,‖·‖c)為錐賦范空間.

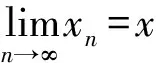
2) 設(shè)(X,‖·‖c) 為錐賦范空間，{xn} 為X中的序列，如果對于每個滿足c?θ的c∈E, 這里總存在一個自然數(shù)N, 使得對于所有的n,m>N, 都有‖xn-xm‖c?c, 那么稱{xn} 為X中的Cauchy列.

3) 若對X中的每個Cauchy列都收斂，稱 (X,‖·‖c)為完備的錐賦范空間.完備的錐賦范空間被稱為錐Banach空間。

定義4[4]設(shè)X是一個非空集合，d:X×X→E, 滿足下列條件：

1)d(x,y)≥θ(?x,y∈X),d(x,y)=θ?x=y;

2)d(x,y)=d(y,x);

3)d(x,y)≤sd(x,z)+sd(z,y)(?x,y,z∈X);

稱d為X上的一個錐b度量，同時稱(X,d) 為錐b度量空間.

1 主要結(jié)果

定義5 設(shè)X是一個向量空間，映射‖·‖c:X→E滿足：

1)‖x‖≥θ(?x∈X),‖x‖c=θ?x=θ;

2)‖x+y‖c≤s‖x‖c+s‖y‖c(?x,y∈X);

3)‖kx‖c=|k|s‖x‖c(?k∈,?x∈X)

稱 ‖·‖c為X上的一個錐b范數(shù)，同時稱(X,‖·‖c)為錐b賦范空間.

完備的錐b賦范空間被稱為錐b-Banach 空間。任意的錐b賦范空間都是錐b度量空間，實(shí)際上，我們可以令d(x,y)=‖x-y‖c.

例1 設(shè)X=R2，P={(x,y):x≥0,y≥0}?R2,及 ‖(x,y)‖c=(|x|2,|y|2).那么(X,‖·‖c)是一個錐b-Banach 空間。

注釋1 定義5推廣了定義2，因?yàn)橹灰诙x5中令s=1，即可得到定義2，而且例1也足以支撐定義5中的錐b-Banach 空間是存在的。

定理1 設(shè)C是錐b-Banach 空間(X,‖·‖c)上的凸閉集，且定義‖x‖c=d(x,0) ，映射T:C→C滿足：

d(x,Tx)+d(y,Ty)≤qd(x,y)

(1)

對任意x,y∈C,0≤q<3s，那么T存在至少一個不動點(diǎn)。

證明 令x0為C中任意一點(diǎn)，定義{xn} ：

(2)

我們可得到d(xn,Txn)=‖xn-Txn‖c=3sd(xn,xn+1)

(3)

結(jié)合(1)式，我們可得到：

3sd(xn-1,xn)+3sd(xn,xn+1)≤qd(xn-1,xn)

d(z,Tz)+3sd(xn,xn+1)≤qd(z,xn)

令n→∞時，我們可得到Tz=z。

注釋2 定理1不僅在空間上推廣了Karapinar[6]的定理2.5，而且推廣了他的定理2.5中壓縮條件的系數(shù)。

定理2 設(shè)C是錐b-Bbanach 空間(X,‖·‖c)上的凸閉集，且定義‖x‖c=d(x,0) ，映射T:C→C滿足：

d(Tx,Ty)+d(x,Tx)+d(y,Ty)≤rd(x,y)

(4)

證明 構(gòu)造定理1中的數(shù)列{xn} ，那么(2)，(3)式都滿足，且

(5)

因?yàn)閐(xn,Txn)-sd(xn,Txn)≤sd(Txn-1,Txn)

考慮到(3)，(5)式，我們得到

3sd(xn,xn+1)-s·2sd(xn-1,xn)≤sd(Txn-1,Txn)

易得 3sd(xn,xn+1)-s·3sd(xn-1,xn)≤sd(Txn-1,Txn)

(6)

令x=xn-1,y=xn代入(4)式中且考慮到(3)，(5)，(6)式，我們得到

我們令x=z,y=xn，代入(4)式，得

d(Tz,Txn)+d(z,Tz)+d(xn,Txn)≤rd(z,xn)

所以Tz=z.

注釋3 定理2不僅在空間上推廣了Karapinar[6]的定理2.6，而且推廣了他的定理2.6中壓縮條件的系數(shù)。

[1]Huang L G, Zhang X.Cone metric space and fixed point theorems of contractive mappings[J]. J Math Anal Appl,2007,332:1468～1476.

[2]Cho S H, Bae J S.Common fixed point theorems for mappings satisfying property (E. A) on cone metric space[J]. Mathematical and Computer Modeling,2011, 53:945～951.

[3]Cho Yeol Je, Saadati Reza, Wang Shenghua.Common fixed point theorems on generalized distance in ordered cone metric spaces[J].J Computers and Mathematics with Applications, 2011,61:1254～1260.

[4]Hussain N,Shah M H.KKM mapping in cone b-metric spaces[J].J Computers and Mathematics with Applications,2011,62:1677～1684.

[5]Abdeljawad T, Turkoglu D, Abuloha M.Some theorems and examples of cone metric spaces[J]. J Comput Anal Appl,2010,12(4): 739～753.

[6]Karapinar E.Fixed point theorems in cone Banach spaces[J]. Fixed Point Theory Appl,2009: 1～9.

Fixedpointtheoremsinconeb-Banachspaces

BAO Bao-guo,LU Dong-hui

(College of Mathematics and Statistics, Hubei Normal University,Huangshi 435002,China)

In this paper,we introduce a concept of cone b-Banach space,using this concept,we prove two fixed point theorems,which generalize the correspondly results obtained by karapinar.

cone Banach space;cone b-Banach space;fixed point

2013—12—29

鮑寶國(1988— )，男，陜西韓城人，碩士研究生，主要從事不動點(diǎn)理論的研究.

O177.91

A

1009-2714(2014)02- 0058- 03

10.3969/j.issn.1009-2714.2014.02.013