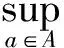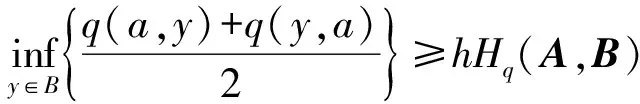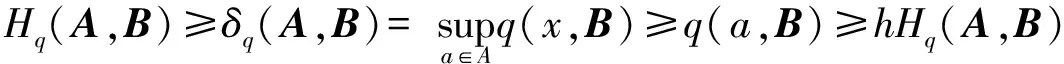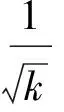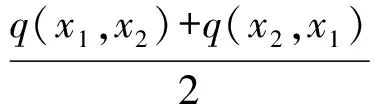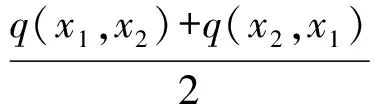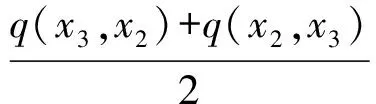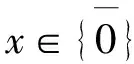擬半Hausdorff度量空間中集值映像的不動點定理
黃東琴, 柴國慶,常思進
(湖北師范學院 數學與統計學院, 湖北 黃石 435002)
擬半Hausdorff度量空間中集值映像的不動點定理
黃東琴, 柴國慶,常思進
(湖北師范學院 數學與統計學院, 湖北 黃石 435002)
給出了擬半Hausdorff度量的定義, 證明擬半度量空間中擬半Hausdorff度量的一些性質, 并利用這些性質證明了擬半度量空間中集值映像的不動點定理.
擬半Hausdorff度量; 不動點; 集值映像
0 引言
半度量空間是對度量空間的推廣, 即把度量空間中的條件d(x,x)=0替換成d(x,x)≤d(x,y),半度量空間的定義和相關性質最先是由Matthews[1,2]提出的. 擬半度量空間又是對半度量空間的推廣, 它是在半度量空間的基礎上減少對稱性這個條件, 即不要求d(x,y)=d(y,x) . 本文是在已有的關于擬半度量空間的研究[1],[3],[4]的基礎上, 給出擬半度量空間中拓撲球的定義和擬半Hausdorff度量的定義, 并且證明了擬半度量空間中的集值映像的不動點定理.
1 預備知識
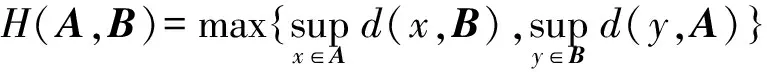
定義2 設X是任意非空集合, 集值映像T:X→CB(X) . 如果存在0≤k<1, 對任意的x,y∈X,有H(Tx,Ty)≤kd(x,y), 我們就說T是壓縮的集值映像.
定義3[6]設X為非空集合, 對任意的x,y,z∈X,如果映像q:X×X→+滿足下列條件:
1) 如果0≤q(x,x)=q(x,y)=q(y,y), 那么x=y,
2)q(x,x)≤q(x,y) ,
3)q(x,x)≤q(y,x) ,
4)q(x,z)+q(y,y)≤q(x,y)+q(y,z) .
則稱q為X上的一個擬半度量,(X,q) 為擬半度量空間.
X上的每個擬半度量都在開球的基礎上都生成一個拓撲. 其中對任意的x∈X,ε>0,我們將開球Bq(x,ε) 定義為
Bq(x,ε)={y∈X:max{q(x,y),q(y,x)} 顯然, 若q是X上的一個半度量, 那么對映像qs:X×X→+定義 ,qs(x,y)=q(x,y)+q(y,x)-q(x,x)-q(y,y), 則qs是X上的一個度量. 定義4[6]設(X,q) 是一個擬半度量空間, 那么有下列命題成立: 4) 設映像f:X→X,x0是X中任意一點. 如果對任意的ε>0, 存在δ>0, 使得f(B(x0,δ))? B(f(x0,ε)) , 那么我們稱映像f在x0連續. 引理1[6]設(X,q) 是一個擬半度量空間,(X,qs) 是相應的度量空間, 那么下面的命題等價. 1) {xn} 是(X,q) 中的柯西列. 2) {xn} 是(X,qs) 中的柯西列. 引理2[2]設(X,q) 是一個擬半度量空間, (X,qs)是相應的度量空間, 那么下面的命題等價. 1) (X,q) 是完備的. 2)(X,qs) 是完備的. 并且 下面的引理對于證明主要結論有重要作用. 引理3[5]設(X,q) 是一個擬半度量空間, 那么下面的命題成立. 1) 如果q(x,y)=0或者q(y,x)=0, 那么x=y. 2) 如果x≠y, 那么q(x,y)>0 且q(y,x)>0 . 設 (X,q)是一個擬半度量空間,CBq(X) 是X的所有非空有界閉子集所組成的集合.其中閉是相對于(X,τq)(τq是由q生成的拓撲)而言, 有界定義如下:任意A?X, 如果存在x0∈X和M≥0, 使得對任意α∈A,有a∈Bq(x0,M),即max{q(a,x0),q(x0,a)} 為了證明本文的主要結論, 我們首先給出一些新的定義. 下面我們給出擬半度量空間中,擬半Hausdorff度量的定義. 定義5 對?A,B∈CBq(X) 和?x∈X, 定義 顯然Hq是X上的一個擬半度量, 稱為X上的擬半Hausdorff度量. (1) (2) 又因為對任意j∈,q(a,xnkj)≥q(a,a),q(xnkj,a)≥q(a,a) (3) 由式(2)和式(3), 我們得到 (4) 另一方面 下面介紹映像δq:CBq(X)×CBq(X)→+的性質. 命題1 設(X,q) 是一個擬半度量空間, 對任意A,B,C∈CBq(X) 以下結論成立: 2)δq(A,A)≤δq(A,B) ; 3)δq(A,B)=0?A?B. 3) 假設δq(A,B)=0. 那么對任意的a∈A,有q(a,B)=0. 由前面的證明得, 對任意的a∈A, 有 命題2 設 (X,q)是一個擬半度量空間,A,B∈CBq(X), 以下結論成立: Hq(A,B)=0?A=B 證明 假設Hq(A,B)=0, 由定義知δq(A,B)=δq(B,A)=0 . 又由命題1的(3)知A?B, 且B?A, 因此A=B. 引理5 設(X,q) 是一個擬半度量空間,A,B∈CBq(X) ,h>1,那么對任意的a∈A, 存在b= b(a)∈B, 使得 證明 如果A=B. 由命題1的(1)知, 設a∈A. 由于h>1, 所以 因此, 取b=a, 引理5成立. 如果A≠B. 假設存在a∈A, 對所有的b∈B, 有 即q(a,B)≥hH4(A,B) . (5) 由于A≠B, 由命題1得Hq(A,B)≠0. 所以由式(5)得h≤1, 這與題設條件矛盾. 定理1[2]設(X,p) 是一個半度量空間,T:X→CBq(X) 是集值映像. 如果存在k∈(0,1), 使對任意的x,y∈X, 有 Hp(Tx,Ty)≤kp(x,y) 那么T有一個不動點. 下面證明我們的主要結論. 定理2 設(X,q) 是一個擬半度量空間,T:X→CBq(X) 是集值映像. 如果存在k∈(0,1) , 使對任意的x,y∈X, 有 Hq(Tx,Ty)≤kq(x,y) 那么T有一個不動點. 又因為Hq(Tx0,Tx1)≤kq(x0,x1),Hq(Tx1,Tx0)≤kq(x1,x0) (6) 由式(6)得 易知, 對x2∈Tx1, 存在x3∈Tx2使得 又因為Hq(Tx1,Tx2)≤kq(x1,x2),Hq(Tx2,Tx1)≤kq(x2,x1) (7) 由式(7)得 繼續下去, 我們得到X中的序列{xn} . 其中xn+1∈Txn且對所有的n≥1 有 (8) 由式(8)和數學歸納法, 對所有的n≥1 , 我們有 (9) 由式(9)和擬部分度量空間的性質4, 對任意的m∈*, 有 由qs的定義知, 對任意的m∈*, 有 qs(xn,xn+m)≤q(xn,xn+m)+(xn+m,xn)→0(n→+∞) (10) 由已知Hq(Txn,Tx*)≤kq(xn,x*) , 所以 (11) 又因為xn+1∈Txn, 所以q(xn+1,Tx*)≤δq(Txn,Tx*)≤Hq(Txn,Tx*) . 另一方面, q(x*,Tx*)≤q(x*,Txn+1)+q(xn,Tx*) (12) 對式(12)兩邊取極限并由式(11)和式(12)得,q(x*,Tx*)=0. 因此, 由式(10)(q(x*,x*)=0)得q(x*,x*)=q(x*,Tx*) . 由引理4知,x*∈Tx*. {0} 和{0,1} 都是(X,q) 中的閉集. 事實上, 如果x∈{0,1,4} , 那么 所以{0} 是X中的閉集. 所以{0,1} 是X中的閉集. 定義映像T:X→CBq(X) 為T(0)=T(1)={0} 和T(4)={0,1} . Hq(Tx,Ty)=Hq({0},{0})=0 所以顯然滿足壓縮條件. 對x∈{0,1},y=4 . 我們有 對x=y=4.我們有 容易看出, 所有情況都滿足定理2的壓縮條件. 這里,x=0 是T的一個不動點. [1]Matthews S G.Partial metric topology[R].Report 212, Department of Computer Science, University of Warwick, 1992. [2]Matthews S G.Partial metric topology[C].General topology and it's Applications, in:Proceedings of the 8th Summer Conference, Queen's College(1992), Annals of the New York Academy of Sciences,1994,728:183~197. [3]Ahmad J,Azam A,Arshad M. Fixed point of multivalued mappings in partial metric spaces[J].Fixed Point Theorey and Applications, 2013, 2013:316. [4]Shatanawi W,Pitea A.Some coupled fixed point theorems in quasi-partial metric spaces[J].Fixed Point Theorey and Applications, 2013, 2013:153. [5]Nadler S B Jr. Multi-valued contraction mappings[J].Pacific J Math,1969,30:475~488. [6]Karapinar E, Erhan I M ,Ozturk A.Fixed point theorems on quasi-partial metric metric spaces[J]. Mathematical and Computer Modelling,2013,57:2442~2448. [7]Aydi H, Abbas M, Vetro C. Partial Hausdorff metric and Nadler's fixed point theorem on partial metric spaces[J]. Topology and its Applications, 2012,159:3234~3242. Fixedpointtheoremformultivaluedmappinginquasi-partialHausdorffmetricspace HUANG Dong-qin, CHAI Guo-qing , CHANG Si-jin (College of Mathematics and Statistics, Hubei Normal University, Huangshi 435002,China) In this paper, we give the definition of the quasi-partial Hausdorff metric and prove some properties of quasi-partial Hausdorff metric in quasi-partial metric space. We also use these properties to prove the fixed point theorem of the multi-valued mappings in quasi-partial metric space. quasi-partial Hausdorff metric; fixed point; multi-valued mappings 2014—01—20 黃東琴(1990— ),女,河南平輿人,碩士研究生,主要研究方向為泛函分析. O177.91 A 1009-2714(2014)02- 0052- 06 10.3969/j.issn.1009-2714.2014.02.012
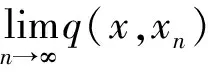
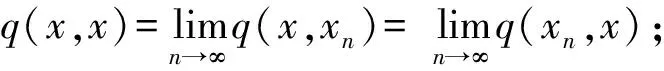

2 擬半度量空間中的擬半Hausdorff度量
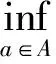


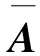

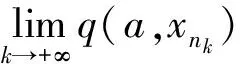





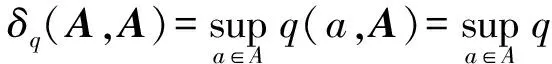


3 主要結果